Презентация на тему Затухающие колебания

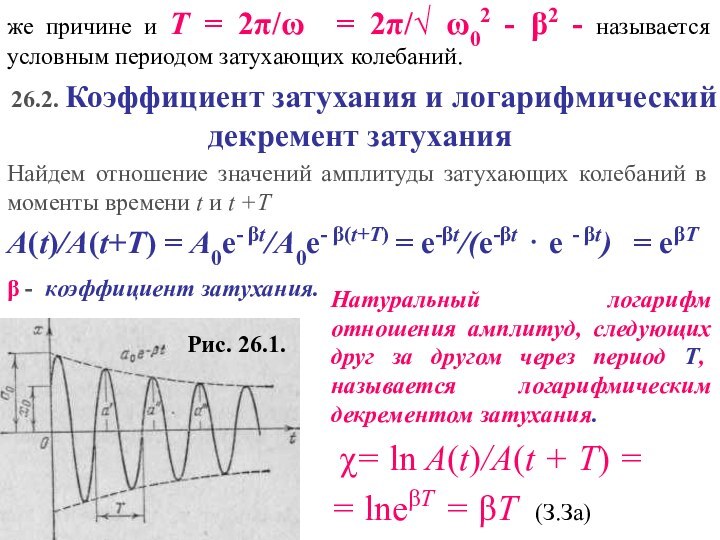
-время, в течение которого амплитуда А
уменьшается в e

раз.
A0 /AΊ = eβτ = e1, откуда βτ = 1, β = 1/τ
Следовательно, коэффициент затухания β - есть физическая
величина, обратная времени, в течении которого амплитуда
уменьшается в е раз. τ - время релаксации.
Пусть Nе число колебаний, после которых амплитуда
уменьшается в e раз, τ - время этих колебаний,
тогда τ = ΝΤ, Τ= τ /Ν и χ = βΤ = τ / τ N = 1/N, χ = 1/N
Следовательно, логарифмический декремент затухания χ есть
физическая величина, обратная числу колебаний, по истечению
которых амплитуда А уменьшается в e раз. Если χ = 0,01,
то N = 100.

на рис. 26.2.



Рис. 26.2.

характеристичес-
кого уравнения становятся вещественными и решение дифферен-
циального уравнения (26.1)

оказывается равным сумме двух
экспонент: х = С1е-λ1t + С2е-λ2t , где λ1= - β +iω, а λ2= - β - iω, а С1 и
С2 - вещественные константы, значения которых зависят от нача-
льных условий (от х0 и υ0). Следовательно движение носит
апериодический (непериодический) характер – выведенная из поло-
жения равновесия система возвращается в положение равновесия,
не совершая колебаний. На рис. 26.26 показано три возможных
способа возвращения системы к положению равновесия при
апериодическом движении. Каким из этих способов приходит

Рис. 26.26.

выведенной из
положения равновесия системе сообщить достаточно сильный
толчок к положению

равновесия. Если, отведя систему из
положения равновесия, отпустить ее без толчка (т.е. с υ0 = 0) или
сообщить ей толчок недостаточной силы (такой, что υ0 окажется
меньше определяемой условием (26.6)), движение будет
Происходить в соответствии с кривой А на рис. 26.26.