- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия пәнінен презентация Параллелепипед.Призма. Пирамида.
Содержание
- 2. Сабақтың мақсаты: Кубтың көлемін, толық бетінің ауданын,
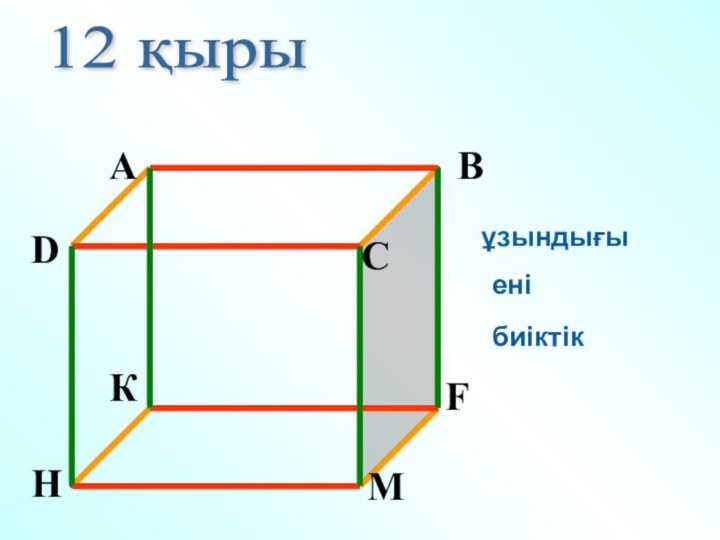
- 3. Тікбұрышты параллелепипед Тіктөртбұрыштармен шектелген кеңістіктік денені тікбұрышты параллелепипед деп атаймыз.
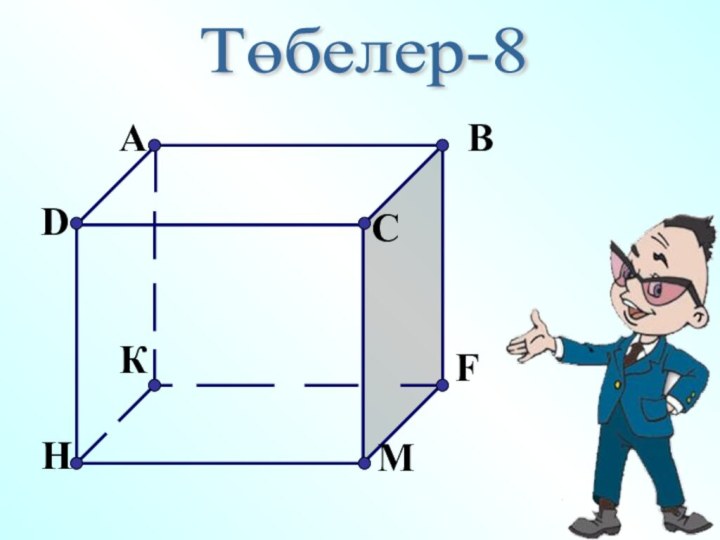
- 4. Төбелер-8
- 5. 12 қырыұзындығыенібиіктік
- 6. Тіктөртбұрыштар6 жағыҚарама қарсы жақтары тең !
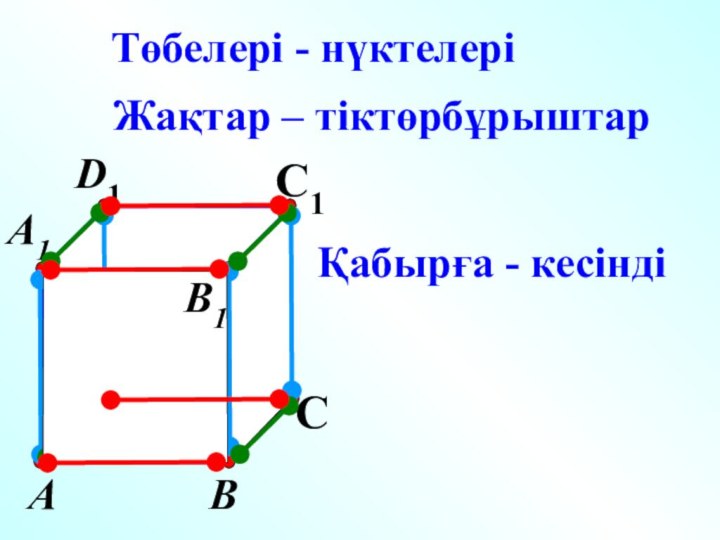
- 7. А В СD1 С1Төбелері - нүктелеріЖақтар – тіктөрбұрыштарҚабырға - кесіндіА1 D В1
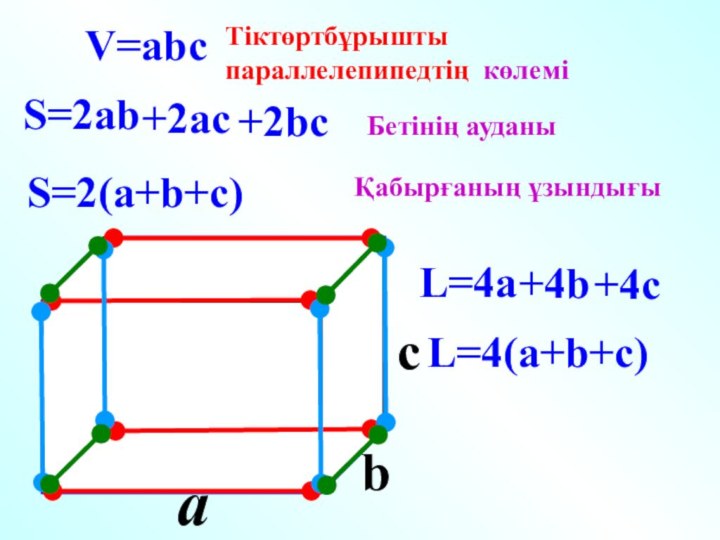
- 8. a c V=abcS=2abS=2(a+b+c)L=4(a+b+c)L=4ab Тіктөртбұрышты параллелепипедтің көлеміБетінің ауданыҚабырғаның ұзындығы+2bc+2ac+4b+4c
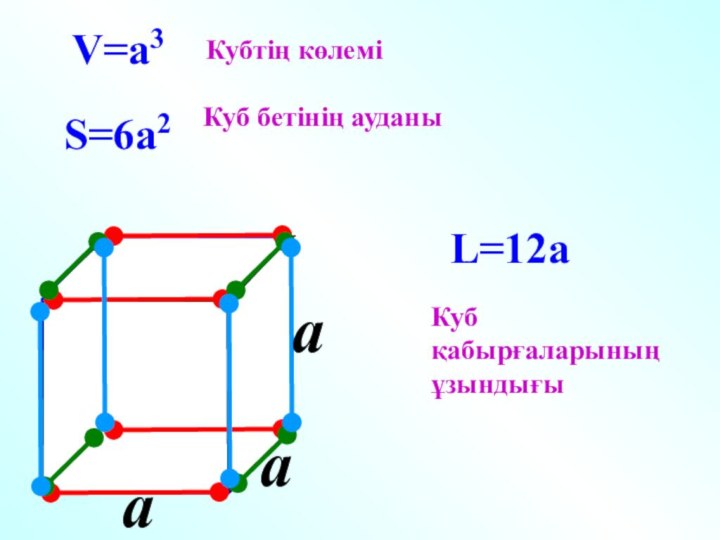
- 9. a V=a3S=6a2L=12aКубтің көлеміКуб бетінің ауданыКуб қабырғаларыныңұзындығыa a
- 10. Қандай заттар тіктөртбұрышты параллелепипедтің формасы түріндеболып табылады?
- 12. 1234
- 13. Қандай геометриялық фигуралар кубтың жақтары болып табылады?
- 14. 23
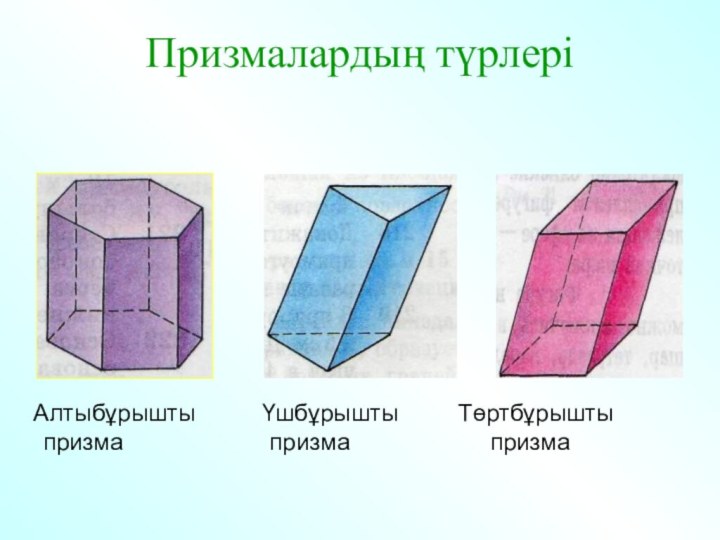
- 15. Призма Табандары параллель жазықтықтарда жататын
- 16. Призманың анықтамасы:А1А2…АnВ1В2Вn– призмаКөпбұрыштар А1А2…Аn и В1В2…Вn –
- 17. Призмалардың түрлері Алтыбұрышты
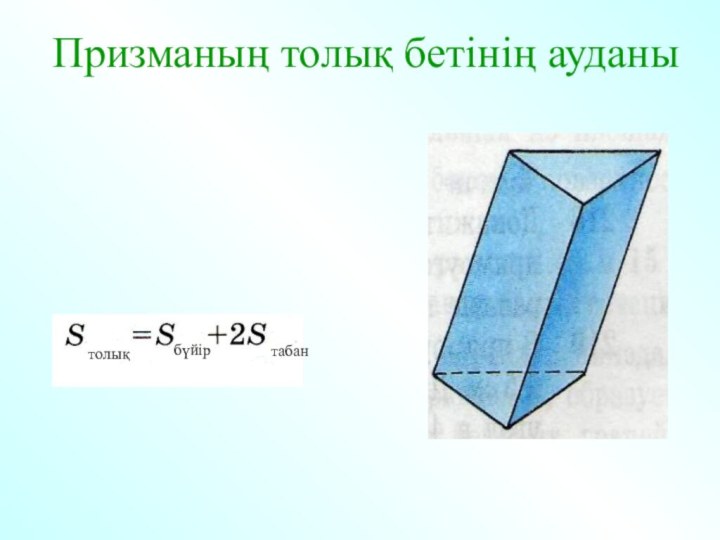
- 18. Призманың толық бетінің ауданытолықбүйіртабан
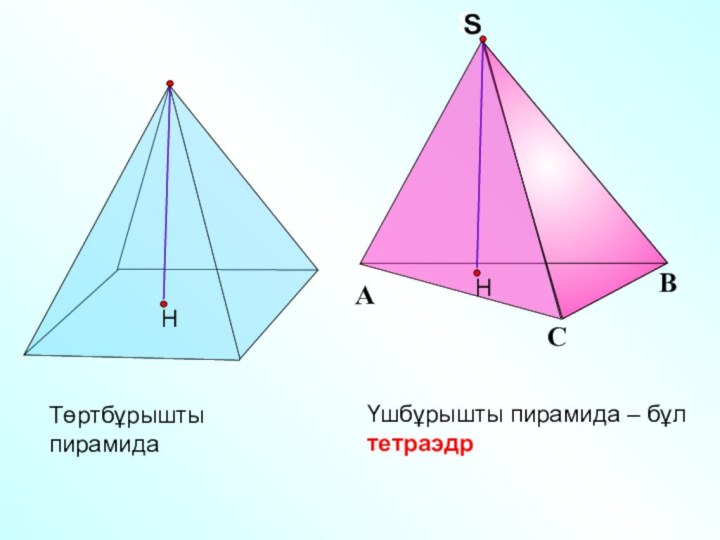
- 19. Пирамида
- 20. А1А2АnРА3Көпбұрыш, n-бұрыштардан А1А2…Аn n үшбұрыштардан, құрылғанпирамида деп
- 21. Үшбұрышты пирамида – бұл тетраэдрТөртбұрышты пирамида
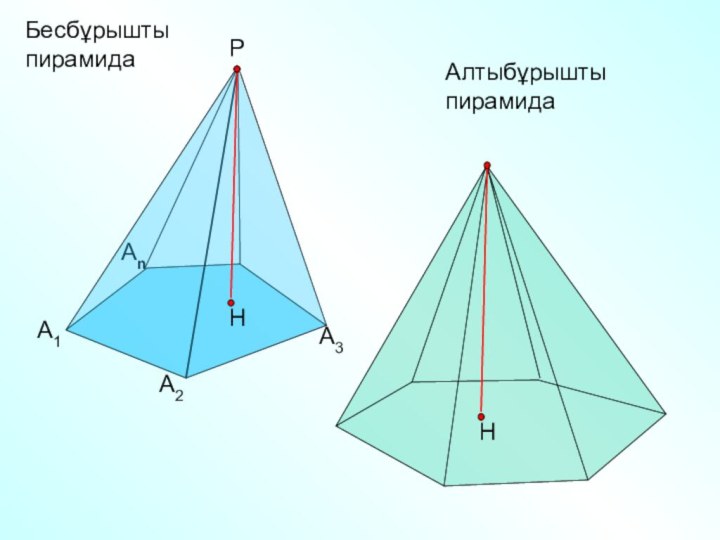
- 22. Бесбұрышты пирамидаА1А2АnРА3Алтыбұрыштыпирамида
- 23. Сұрақтар 1. Тік призманың ең аз
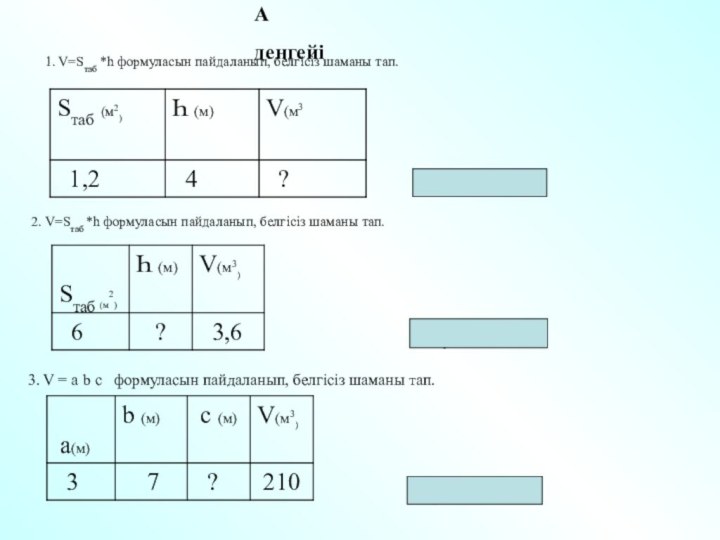
- 24. 1. V=Sтаб *h формуласын пайдаланып, белгісіз шаманы
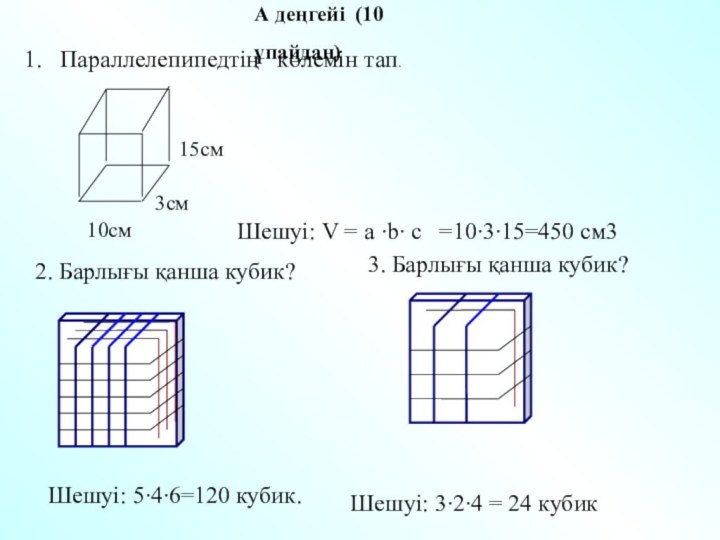
- 25. 1. Параллелепипедтің көлемін тап.
- 26. В деңгей №274 (1) есеп №277 (2) есеп №277 (1) есеп №275 (1) есеп
- 27. С деңгей №275 (2) есеп №278 есеп №276 есеп
- 29. D V=8*4*5=160(см3)А В СD1 С1А1 В1 Параллелепипедті
- 30. Осы фигуралардың көлемдерін табыңыз
- 31. Тексеру:1)V=12)V=63)V=84)V=187)V=725)V=86)V=24
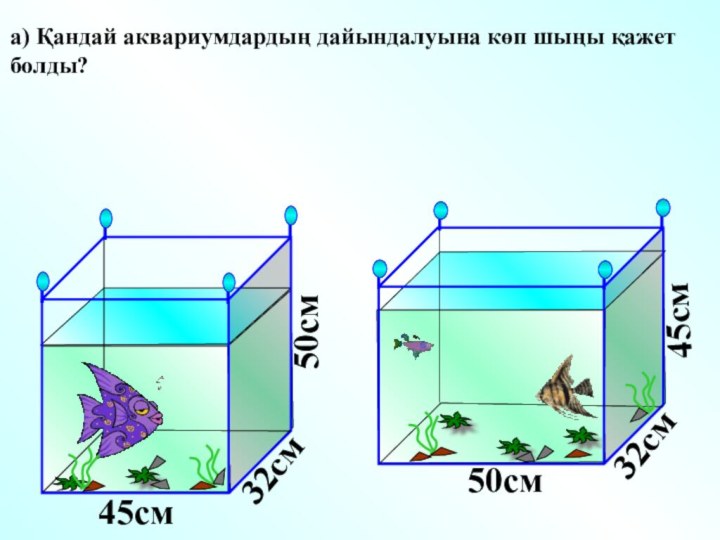
- 32. а) Қандай аквариумдардың дайындалуына көп шыңы қажет болды?45см 45см 50см 50см 32см 32см
- 33. 4,8м 10,25м 7,5м
- 34. АА1ВСDEFF1E1D1С1В1Дененің көлемін анықтаңыз, егер АА1=АВ=АF=20см, ВС=12 см,
- 35. Фигураның көлемін анықтау үшін формуланы құрастырыңыз.ycxab1) abx
- 36. Фигураның көлемін есептеу үшін формуласын құрастырыңыз.xaax1) a3
- 37. Үй жұмысы1.№279 есеп. 2. Параллелепипед, призма, пирамида
- 38. Скачать презентацию
- 39. Похожие презентации
Сабақтың мақсаты: Кубтың көлемін, толық бетінің ауданын, қырын, қарама -қарсы жақтарының арақашықтығың, қырының ұзындығын, пирамиданың, тік призманың толық бетінің ауданын табуды игерту. Сабақтың білімділік мақсаты: Параллелепипед, призма, пирамида жайлы түсініктерін қалыптастыру; Сабақтың тәрбиелік



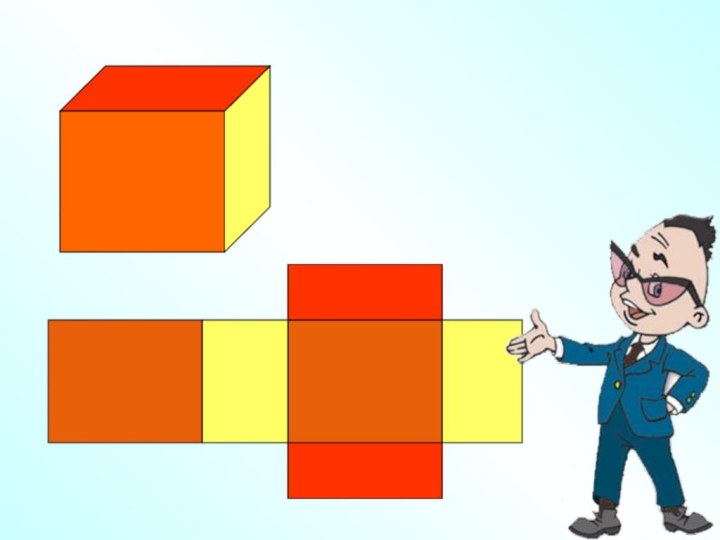
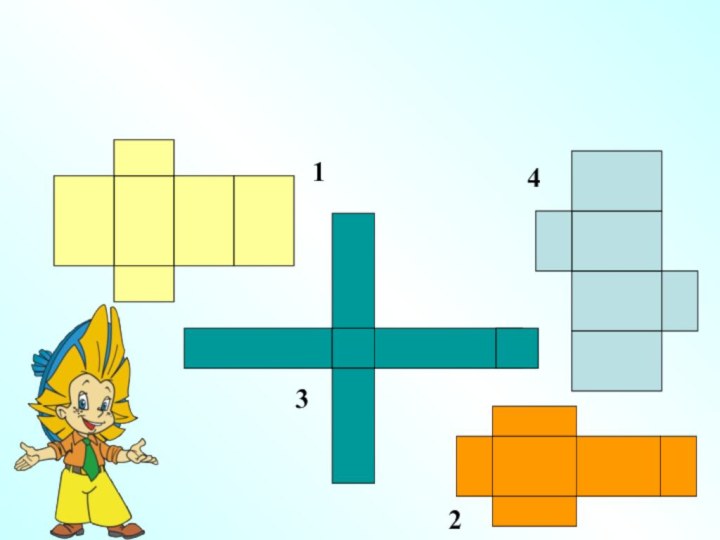

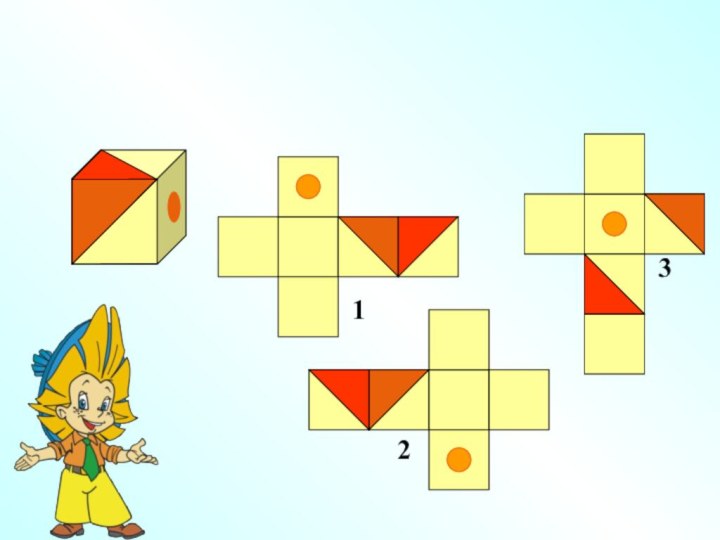



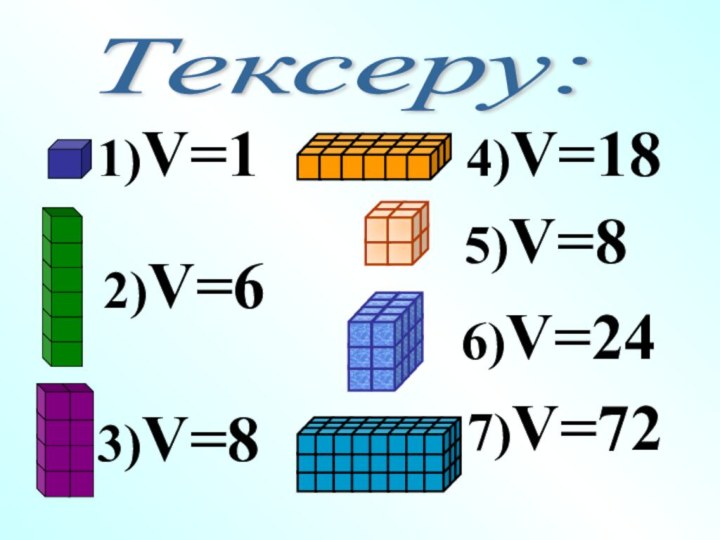




Слайд 3
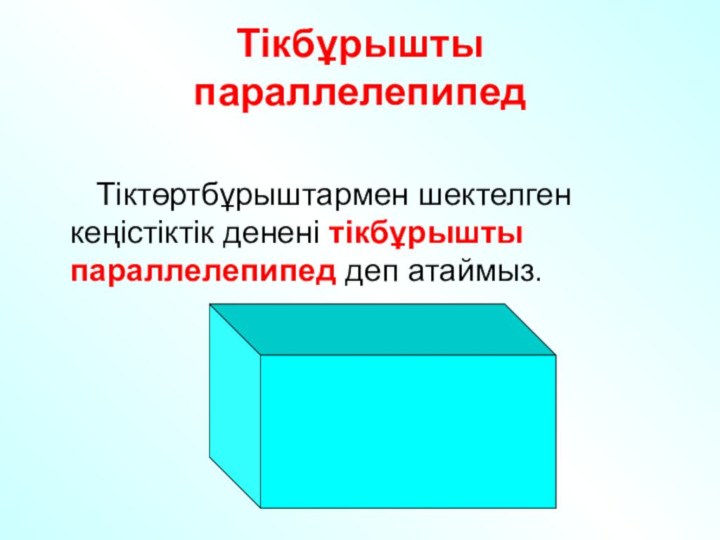
Тікбұрышты
параллелепипед
Тіктөртбұрыштармен шектелген кеңістіктік денені
тікбұрышты параллелепипед деп атаймыз.
Слайд 8
a
c
V=abc
S=2ab
S=2(a+b+c)
L=4(a+b+c)
L=4a
b
Тіктөртбұрышты
параллелепипедтің көлемі
Бетінің ауданы
Қабырғаның ұзындығы
+2bc
+2ac
+4b
+4c
Слайд 15
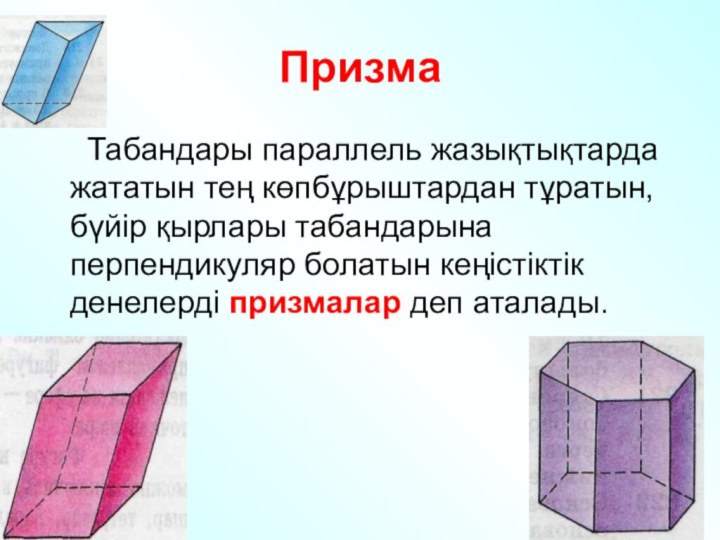
Призма
Табандары параллель жазықтықтарда жататын тең
көпбұрыштардан тұратын,бүйір қырлары табандарына перпендикуляр болатын кеңістіктік денелерді призмалар
деп аталады.
Слайд 16
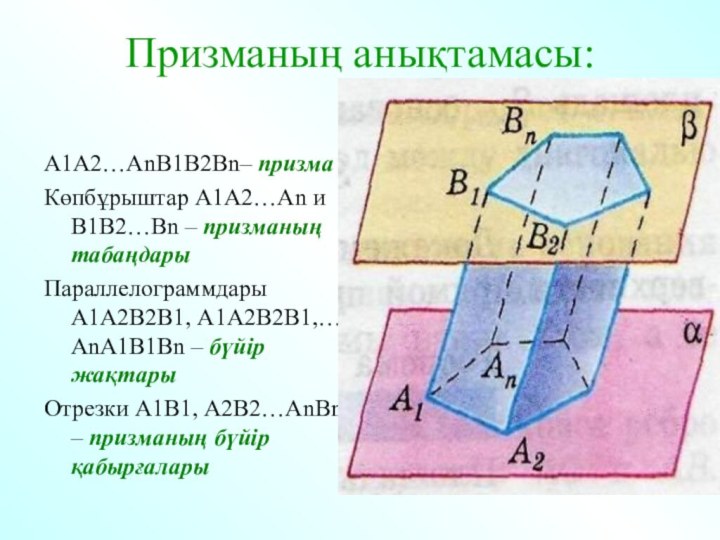
Призманың анықтамасы:
А1А2…АnВ1В2Вn– призма
Көпбұрыштар А1А2…Аn и В1В2…Вn – призманың
табаңдары
Параллелограммдары А1А2В2В1, А1А2В2В1,… АnА1В1Вn – бүйір жақтары
Отрезки А1В1, А2В2…АnBn
– призманың бүйір қабырғалары
Слайд 20
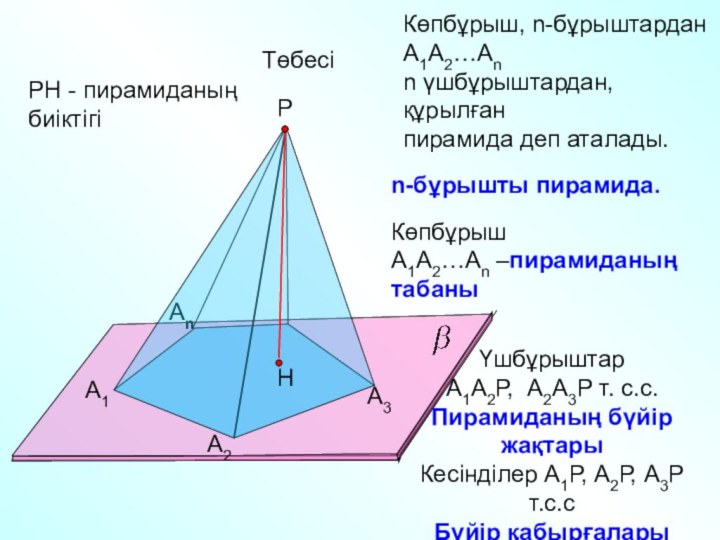
А1
А2
Аn
Р
А3
Көпбұрыш, n-бұрыштардан А1А2…Аn
n үшбұрыштардан,
құрылған
пирамида деп аталады.
Төбесі
РН
- пирамиданың биіктігі
n-бұрышты пирамида.
Көпбұрыш
А1А2…Аn –пирамиданың
табаны
Үшбұрыштар
А1А2Р, А2А3Р т. с.с.
Пирамиданың бүйір жақтары
Кесінділер А1Р, А2Р, А3Р
т.с.с
Бүйір қабырғалары
Слайд 23 Сұрақтар 1. Тік призманың ең аз болғанда қанша
жағы болуы мүмкін? 2. Сегізжақты тік призманың табандары қандай көпбұрыштар
болуы мүмкін? 3. Бесжақты пирамиданың табаны қандай көпбұрыш болуы мүмкін? 4. Бесбұрышты тік призманың қанша төбесі, жағы, қырлары бар? 5. Алтыбұрышты пирамиданың қанша төбесі, жағы, қырлары бар?Жауабы: 5
Жауабы: Сегізбұрыш
Жауабы: Бесбұрыш
Жауабы: 10 төбесі, 7 жағы, 15 қыры
Жауабы: 7 төбесі. 7 жағы, 12 қыры
Слайд 24 1. V=Sтаб *h формуласын пайдаланып, белгісіз шаманы тап.
Жауабы: 0,6 м
2. V=Sтаб *h формуласын пайдаланып, белгісіз
шаманы тап. А деңгейі
3. V = a b c формуласын пайдаланып, белгісіз шаманы тап.
Жауабы: 10 м
Слайд 25 1. Параллелепипедтің көлемін тап.
2. Барлығы қанша кубик?
Шешуі: 5∙4∙6=120 кубик.
15см
3см
10см
Шешуі: V = a ∙b∙ c =10∙3∙15=450 см3
3. Барлығы қанша кубик?
Шешуі: 3∙2∙4 = 24 кубик
А деңгейі (10 ұпайдан)
Слайд 28
Тест есептері
1) Кубтың көлемі 125 см 3. Кубтың қырын тап.
А) 25см В) 15 см С) 5 см Д) 125 см
2) Параллелепипедтің табан ауданы 12 см2, биіктігі 7см. Көлемін тап.
А) 84см3 В) 19 см3 С) 38 см3 Д) 168см3
3) Тікбұрышты параллелепипедтің үш өлшемі берілген. а= 3cм, в=8см, с=10см. Параллелепипедтің толық бетін тап.
А) 110см2 В) 134 см2 С) 240 см2 Д) 268см2
4) Пирамиданың табанының ауданы 16 м2 , бүйір бетінің ауданы 24м2. Пирамиданың толық бетін тап.
А) 40м2 В) 64м2 С) 58м2 Д) 88м2
5) Тік призманың табан қабырғасы 5 см болатын дұрыс үшбұрыш. Призманың бүйір қыры 16 см. Призманың бетінің ауданын тап.
А) 80 см2 В) 240 см2 С) 400 см2 Д) 21 см2
Слайд 29
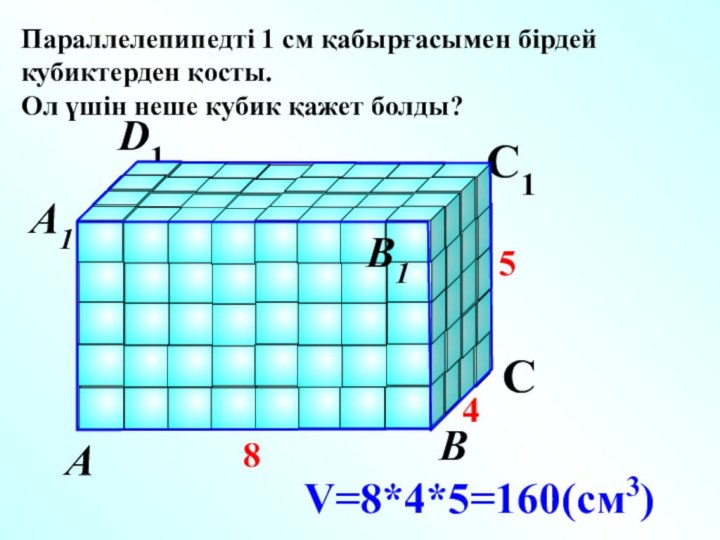
D
V=8*4*5=160(см3)
А
В
С
D1
С1
А1
В1
Параллелепипедті 1
см қабырғасымен бірдей кубиктерден қосты.
Ол үшін неше кубик қажет
болды?
Слайд 34
А
А1
В
С
D
E
F
F1
E1
D1
С1
В1
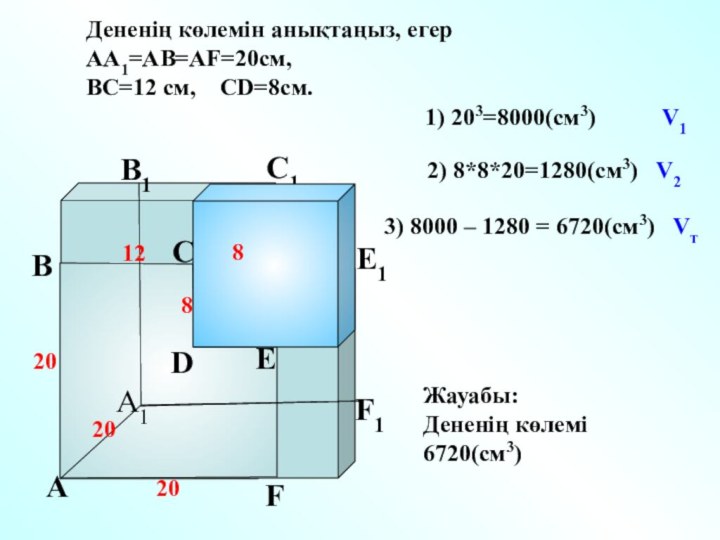
Дененің көлемін анықтаңыз, егер АА1=АВ=АF=20см,
ВС=12 см,
СD=8см.
12
8
20
20
1) 203=8000(см3) V1
8
20
2) 8*8*20=1280(см3)
V23) 8000 – 1280 = 6720(см3) Vт
Жауабы:
Дененің көлемі 6720(см3)
Слайд 35
Фигураның көлемін анықтау үшін формуланы құрастырыңыз.
y
c
x
a
b
1) abx
V1
2) (a-y)(x-c)b
V23) abc – (a-y)(x-c)b Vф
Слайд 36
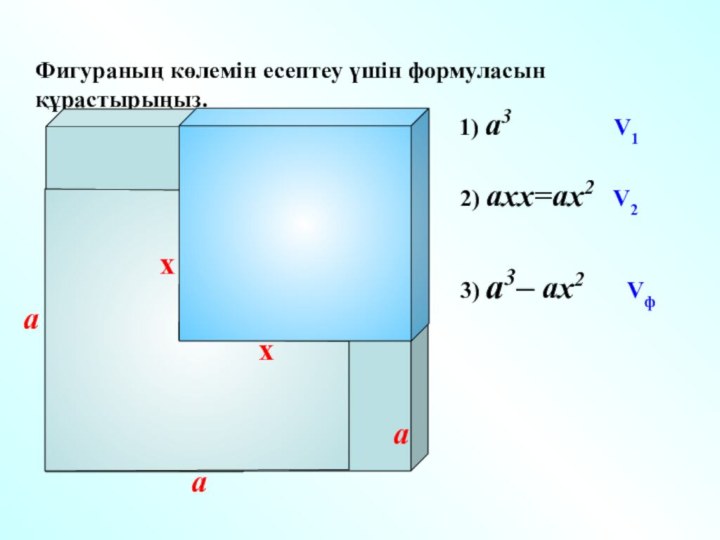
Фигураның көлемін есептеу үшін формуласын құрастырыңыз.
x
a
a
x
1) a3
V1
a
2) aхх=ах2
V23) а3– ах2 Vф