- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площади по геометрии
Содержание
- 2. ГИПОТЕЗА Можно ли, показав несколько способов
- 4. Исторические сведения.
- 5. Понятие площади многоугольника. Понятие площади известно
- 6. Единицы площадей. Единица измерения
- 9. Способ нахождения площадей с помощью палетки
- 10. Работа с первоклассникамиВычисление площадей фигур
- 12. Исследование 1Для исследований была взята плотная бумага
- 13. Нахождение площади кругаДля того чтобы убедиться в
- 14. Исследование 2Расчёт сметыКаждый человек представляет, что такое
- 15. Формулы для вычисленияПлощадь прямоугольника равна произведению его
- 18. m = 18 000г = 18кгC =
- 20. Вывод: Я научилась находить площадь фигур различными
- 21. Венгерским математиком Ф.Бойяи и немецким любителем математики
- 22. Скачать презентацию
- 23. Похожие презентации
ГИПОТЕЗА Можно ли, показав несколько способов измерения площадей, убедить окружающих в том, что геометрические знания необходимы каждому человеку.





















Слайд 3
Основная цель работы-
показать практическую значимость геометрии
и необходимость умения находить площади фигур в жизни.
Слайд 4
Исторические сведения.
Площадь, одна из основных величин, связанных с геометрическими
фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т.е. квадратов со стороной, равной единице длины. Вычисление площади было уже в древности одной из важнейших задач практической геометрии. За несколько столетий до нашей эры греческие ученые располагали точными правилами вычисления площади. Правильный подход к их решению был найден не сразу. Древние вавилоняне полагали, что площадь всякого четырехугольника равна произведению полу сумм противоположных сторон. Но уже древние греки умели правильно находить площади многоугольников. Когда каменщики определяют площадь прямоугольной стены дома, они перемножают высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Площадь составной фигуры не изменяется, если ее части расположить по-другому, но опять без пересечения. Поэтому можно, исходя из формулы площади прямоугольника, находить формулы площадей других фигур. Фигуру, площадь которой требуется измерить, вычерчивают на миллиметровой бумаге и подсчитывают сначала число укладывающихся в границы фигуры сантиметровых квадратиков, потом миллиметровых. Если бы существовала миллиметровая бумага с делениями, кратными сколько угодно высокой степени десятки, такая процедура, продолженная неограниченно долго, приводила бы к точному значению площади. Методы нахождения площадей произвольных фигур дает интегральное исчисление. Существуют и механические приборы для вычисления площадей плоских фигур –так называемые планиметры.Первой из сохранившихся рукописей, в которых излагаются правила измерения площадей, была «Книга сошного письма», самый древний экземпляр, который относится к 1629 году, хотя имеются указания, что оригинал был составлен при Иване Грозном в 1556 году. В этой книге имеется глава «О земном верстании, как земля верстать». В ней, к сожалению, содержится много ошибочного материала в способах измерения площадей. Возможно, они появились в результате искажений во время переписывания от руки. Приходится признать, что уровень знаний был невысоким, хотя не хочется считать россиян шестнадцатого и семнадцатого столетий менее грамотными, чем древние египтяне. Тем более ярким подтверждением тому служат исключительные по красоте архитектурные памятники того времени, такие, как собор Василия Блаженного, построенный в 1553-1560 г.г. при Иване Грозном русскими «мастерами каменных дел Постником, Яковлевым и Бармой.
Слайд 5
Понятие площади многоугольника.
Понятие площади известно из
повседневного опыта. Каждый понимает смысл слов: площадь комнаты -
16 м2, 25 ар - площадь садового участка.Площадь многоугольника- это величина той части плоскости, которую занимает многоугольник.
Измерение площадей проводится с помощью выбранной единицы измерения. За единицу измерения площадей принимают квадрат.
Площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.
Если два многоугольника равны, то единица измерения площадей и ее части укладываются в таких многоугольниках одинаковое число раз.
Слайд 6
Единицы площадей.
Единица измерения отрезков
см, единица измерения площадей - квадрат со стороной 1
см. Такой квадрат называется квадратным сантиметром и обозначается 1 см2.1см2 = 1см•1 см =10мм•10мм =100 мм2
1дм2 = 1дм•1 дм =10см•10см =100 см2
1м2 = 1м•1 м =10дм•10дм =100 дм2
1см2
1м2
1дм2
1мм²
Слайд 7
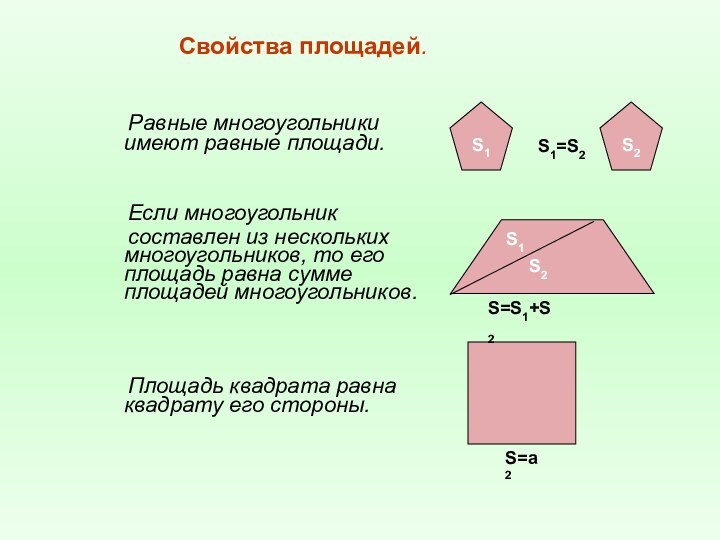
Свойства площадей.
Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей многоугольников.
Площадь квадрата равна квадрату его стороны.
S1
S2
S2
S1
S=а2
S1=S2
S=S1+S2
Слайд 8
Задачи исследования:
-измерить площадь произвольной фигуры с
помощью палетки;-составить алгоритм взвешивания площадей плоских фигур;
-найти площадь круга взвешиванием;
- рассчитать себестоимость ремонта дачного домика.
Слайд 9
Способ нахождения площадей с помощью палетки
В начальном курсе математики учащиеся
измеряют площади фигур с помощью палетки таким образом: подсчитывают число квадратов, которые лежат внутри фигуры, и число квадратов, через которые проходит контур фигуры. Затем второе число делят пополам и прибавляют к первому. Полученную сумму считают площадью фигуры .Палетка позволяет измерить площадь фигуры с определенной точностью.
Чтобы получить более точный результат, нужно взять палетку с более мелкими
квадратами.
Слайд 11
Сколько весит площадь?
1.Взять лист
плотной бумаги.
2.Взвесить этот лист, получим массу - m [ г ].
3.Измерить длину и ширину листа;найти площадь S [ см² ]. 4. Разделить массу на площадь;
получаем массу 1 см² бумаги, т.е.
поверхностную плотность σ [ г / см² ]. 5. Нарисовать на этом же листе любую фигуру и вырезать её.
6.Взвесив фигуру,получаем массу mф. 7. Находим площадь по формуле Sф = mф / σ.
Слайд 12
Исследование 1
Для исследований была взята плотная бумага из
альбома для рисования. Ее размеры измеряем рулеткой с точностью
до 1 мм. Длина листа a = 42 см Ширина листа b = 30 см Площадь листа S = a·b, S=1,26·10³ см² Взвесим лист на весах с точностью до 10 мг. Масса листа m = 28,43 гПоверхностная плотность бумаги σ = m/S, σ = 0,0226 г/см².
Слайд 13
Нахождение площади круга
Для того чтобы убедиться в правильности
выбранного метода, измерим площадь другой плоской фигуры – круга.
На таком же листе формата А3 нарисуем круг. Его радиус равен R = 9,9 см. Вырежем его и взвесим. Масса круга m = 6,9 г.Площадь круга S = m/σ, S =6,9/0,0226= 305,3 см². Экспериментально определяем значение π
Площадь круга S = π·R², π = S/R², имеем π ≈ 3,13. Более точное значение π ≈ 3,14, отличается от полученного на 0,01. Это убеждает нас в правильности выбранного метода измерения площади плоской фигуры.
Слайд 14
Исследование 2
Расчёт сметы
Каждый человек представляет, что такое площадь
комнаты, площадь участка земли, площадь поверхности, которую надо покрасить.
Он также понимает, что площадь квартиры складывается из площади комнат и площади других помещений.Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют определенный класс фигур. В своём исследовании я буду пользоваться формулами для нахождения площадей многоугольников.
Слайд 15
Формулы для вычисления
Площадь прямоугольника равна произведению его смежных
сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника
равна половине произведения его основания на высоту.Площадь ромба равна половине произведения его диагоналей.
Площадь трапеции равна половине произведения суммы ее оснований на высоту.
h
а
S=h·а
S= ½h·а
h
а
d1
d2
S=d1·d2
S=а•в
h
а
в
S=½(а+в)· h
Слайд 18
m = 18 000г = 18кг
C = 1
170 руб
Покрась крышу и стены
S =120 м2
m = 36
000г = 36 кгC = 2 340 руб
Слайд 20
Вывод:
Я научилась находить площадь фигур различными способами
и научила этому учащихся начальных классов, своих одноклассников и
родителей.Своей работой я постаралась убедить окружающих в необходимости изучения геометрии, как науки.
В рамках своей работы предлагаю продолжить работу по поиску новых методов нахождения площадей. Мне хочется научиться находить площади с помощью интегрального исчисления. Думаю увлечь данной работой своих будущих однокурсников.
Слайд 21
Венгерским математиком Ф.Бойяи и немецким любителем математики П.Гервином
была доказана теорема: любые два многоугольника равносоставлены. Другими словами,
если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.Теорема Бойяни - Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.