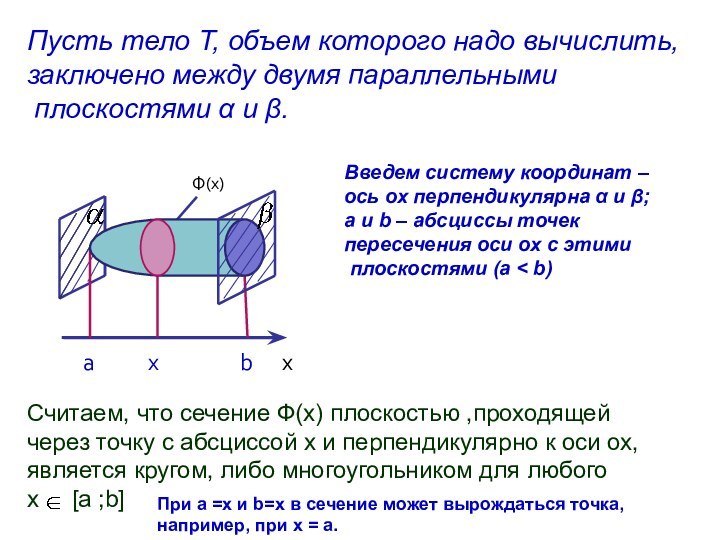
между двумя параллельными
плоскостями α и β.
Введем систему координат
–ось ох перпендикулярна α и β;
а и b – абсциссы точек
пересечения оси ох с этими
плоскостями (а < b)
a x b x
Ф(x)
Считаем, что сечение Ф(х) плоскостью ,проходящей через точку с абсциссой х и перпендикулярно к оси ох, является кругом, либо многоугольником для любого
х [a ;b]
При а =х и b=x в сечение может вырождаться точка,
например, при х = а.