- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллелепипед
Содержание
- 2. Развитие геометрии.Начало геометрии было положено в древности
- 3. В XVII в. Декарт благодаря методу координат
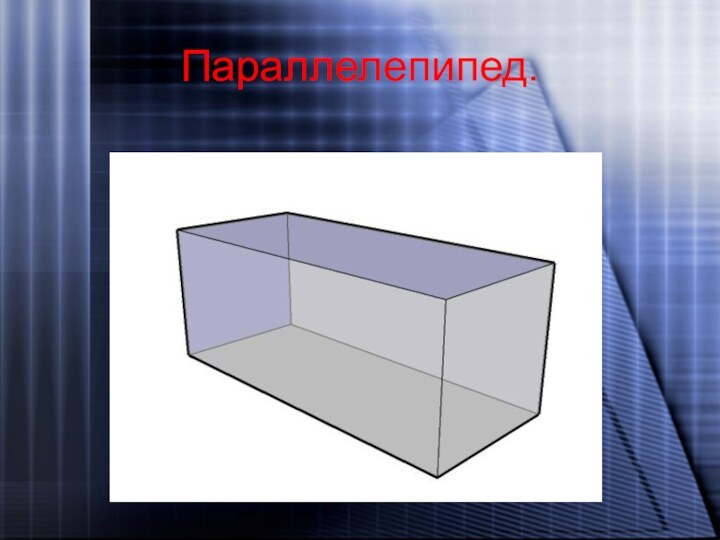
- 4. Параллелепипед.
- 5. Параллелепи́пед - (от греч. παράλλος — параллельный
- 6. Основные элементы параллелепипеда:1.Две грани параллелепипеда, не имеющие
- 7. У параллелепипедов и только у них любую
- 8. Свойства параллелепипеда:1.Противоположные грани параллелепипеда равны и параллельны.2.Все
- 9. Теорема: У параллелепипеда противолежащие грани параллельны и
- 10. Теорема: Параллелепипед симметричен относительно середины его диагонали.Важные
- 11. Произвольный параллелепипед.Объём и соотношения в наклонном параллелепипеде
- 12. Объем параллелепипеда:
- 13. В параллелепипед можно вписать тетраэдр. Объем такого тетраэдра равен 1/3 части объема параллелепипеда.
- 14. Вот так параллелепипед выглядит в развертке.
- 15. Различается несколько типов параллелепипедов:1.Прямоугольный параллелепипед. 2.Прямой параллелепипед. 3.Наклонный параллелепипед.4.Куб.
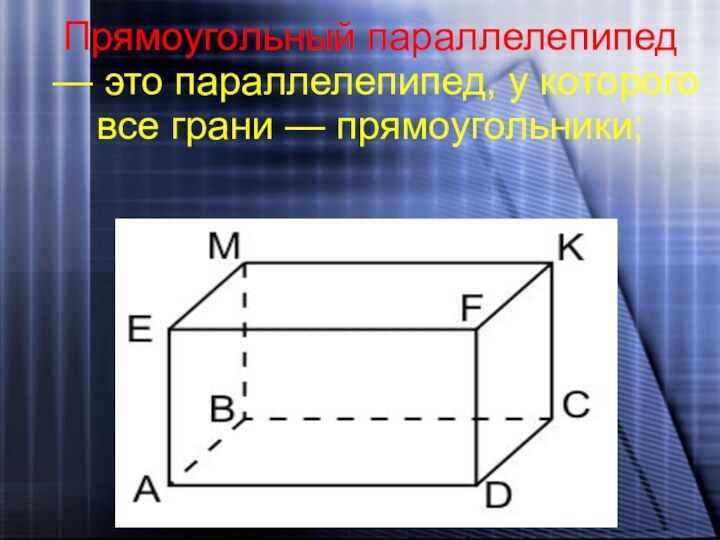
- 16. Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники;
- 17. Вывод формулы объёма прямоугольного параллелепипеда, измерения
- 18. Свойства диагоналей прямоугольного параллелепипеда:Диагонали параллелепипеда пересекаются в
- 19. Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
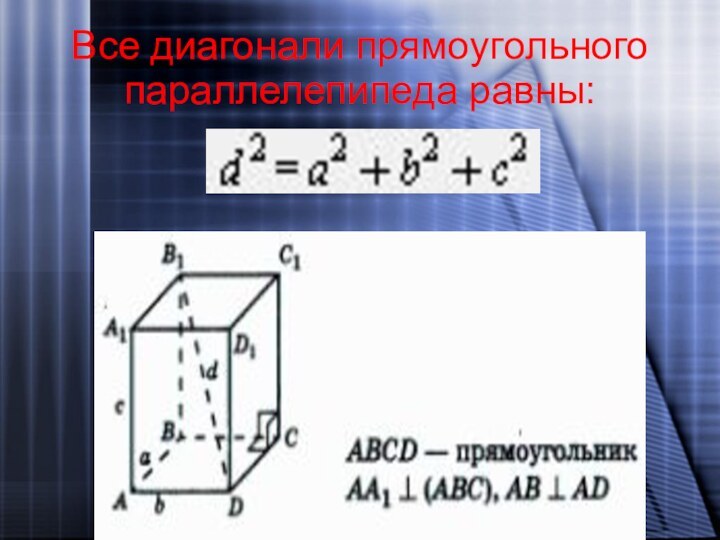
- 20. Все диагонали прямоугольного параллелепипеда равны:
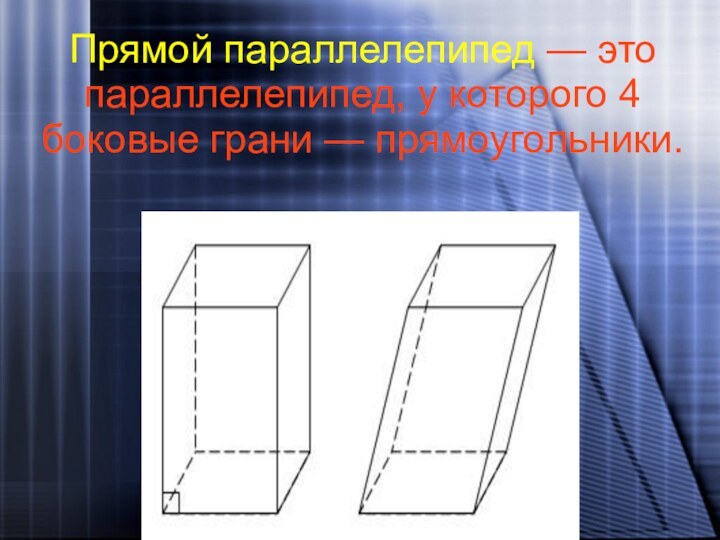
- 21. Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
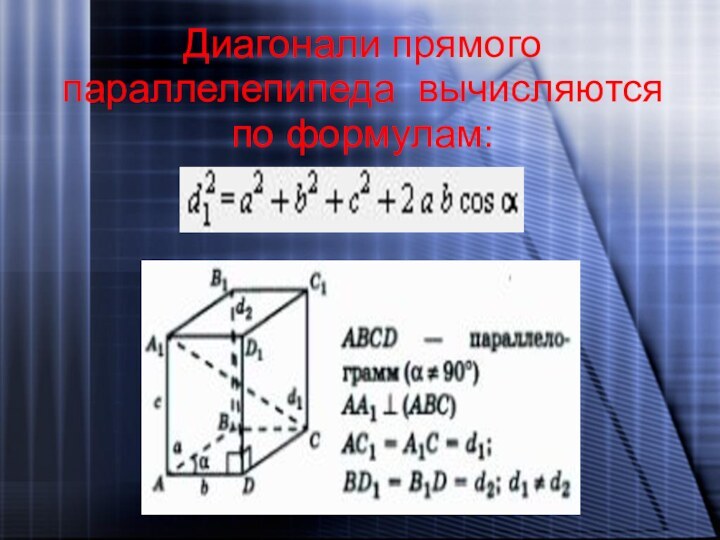
- 22. Диагонали прямого параллелепипеда вычисляются по формулам:
- 23. Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основанию.
- 24. Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
- 25. Свойства куба.1.Четыре сечения куба являются правильными шестиугольниками
- 26. Диагональю куба- называют отрезок, соединяющий две вершины,
- 27. В свое время, в1919 году, Чарльз Форт
- 28. Сайты с информацией: http://www.fmclass.ru/math.php?id=4862626930263 http://ru.wikipedia.org http://www.fxyz.ru
- 29. Скачать презентацию
- 30. Похожие презентации
Развитие геометрии.Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств.





















Слайд 3 В XVII в. Декарт благодаря методу координат сделал
возможным изучение свойств геометрических фигур с помощью алгебры. С
этого времени начала развиваться аналитическая геометрия.В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Слайд 5
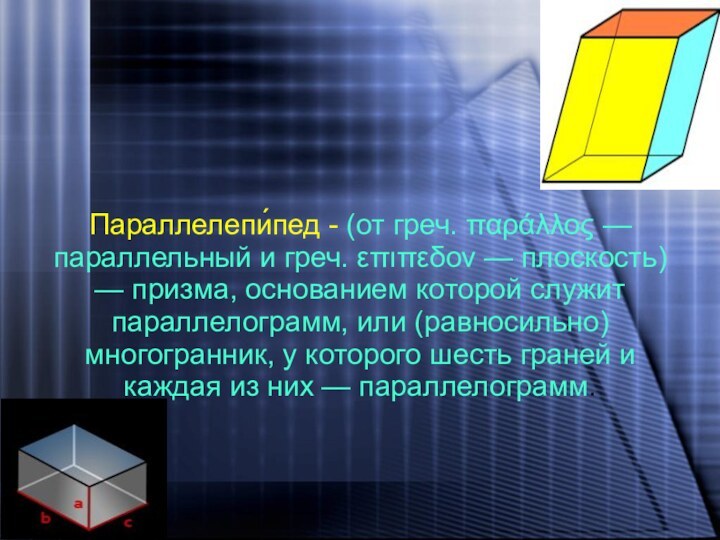
Параллелепи́пед - (от греч. παράλλος — параллельный и
греч. επιπεδον — плоскость) — призма, основанием которой служит
параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Слайд 6
Основные элементы параллелепипеда:
1.Две грани параллелепипеда, не имеющие общего
ребра, называются противоположными, а имеющие общее ребро — смежными.
2.Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными.
3.Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
4.Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
Слайд 7 У параллелепипедов и только у них любую пару
параллельных граней можно принять за основания. В зависимости от
выбора оснований можно рассмотреть три высоты.
Слайд 8
Свойства параллелепипеда:
1.Противоположные грани параллелепипеда равны и параллельны.
2.Все четыре
диагонали параллелепипеда пересекаются в одной точке и делятся этой
точкой пополам.3.Боковые грани прямого параллелепипеда — прямоугольники.
4.Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Слайд 9
Теорема:
У параллелепипеда противолежащие грани параллельны и равны.
Доказательство
Возьмем любые две противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`.
Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны. Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны.
Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
Слайд 10
Теорема: Параллелепипед симметричен относительно середины его диагонали.
Важные свойства
параллелепипеда:
1.Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий
через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.2. Противолежащие грани параллелепипеда параллельны и равны.
Слайд 11
Произвольный параллелепипед.
Объём и соотношения в наклонном параллелепипеде часто
определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной
величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения
Слайд 13
В параллелепипед можно вписать тетраэдр.
Объем такого тетраэдра
равен 1/3 части объема параллелепипеда.
Слайд 15
Различается несколько типов параллелепипедов:
1.Прямоугольный параллелепипед.
2.Прямой параллелепипед.
3.Наклонный
параллелепипед.
4.Куб.
Слайд 17 Вывод формулы объёма прямоугольного параллелепипеда, измерения которого выражены
целыми числами:
Пусть нам нужно вычислить объём прямоугольного параллелепипеда, длина
основания которого равна 20 см, ширина — 12 см и высота параллелепипеда—5 см. Площадь основания этого параллелепипеда будет равна 20 • 12 = 240 (кв. см). Значит, на его основании в один слой можно уложить 240 кубических сантиметров. Всего таких слоев будет пять. Объём данного параллелепипеда будет равен
240 • 5 = 1200 (куб. см).
Если длину основания прямоугольного параллелепипеда обозначим через а, ширину его — через b и высоту параллелепипеда— через с, то получим формулу:
V = аbс, где V — объём прямоугольного параллелепипеда
Слайд 18
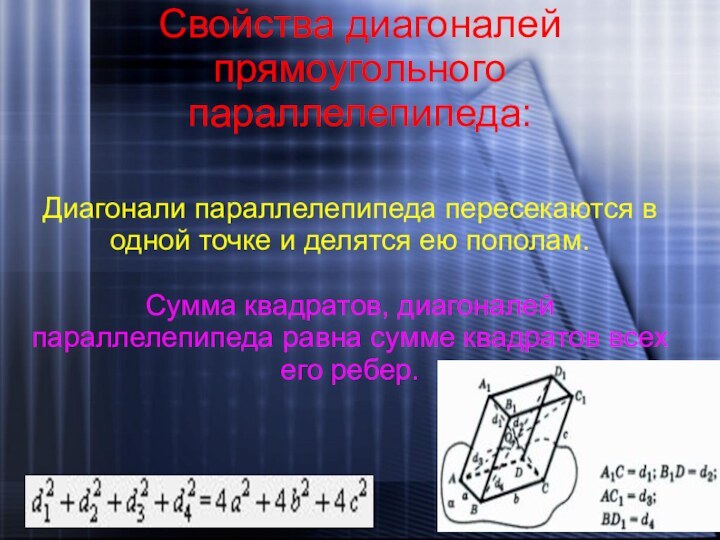
Свойства диагоналей прямоугольного параллелепипеда:
Диагонали параллелепипеда пересекаются в одной
точке и делятся ею пополам.
Сумма квадратов, диагоналей параллелепипеда
равна сумме квадратов всех его ребер.Слайд 19 Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей
трех граней этого параллелепипеда:
S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
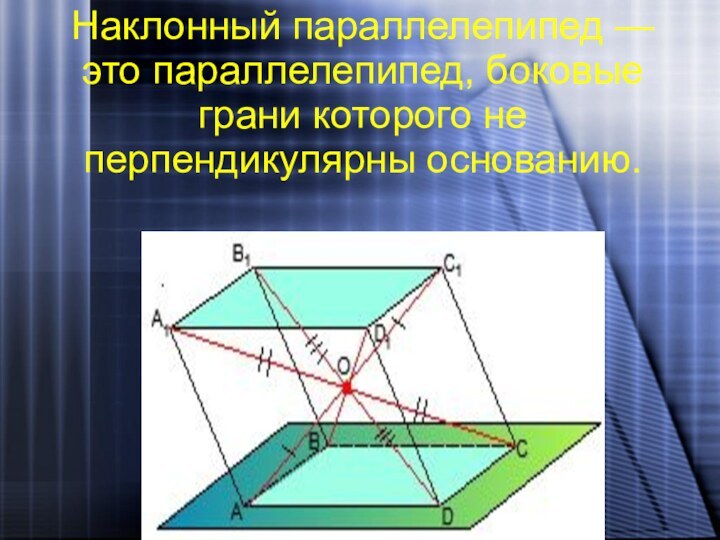
Слайд 23 Наклонный параллелепипед — это параллелепипед, боковые грани которого
не перпендикулярны основанию.
Слайд 24 Куб — это прямоугольный параллелепипед с равными измерениями.
Все шесть граней куба — равные квадраты.
Слайд 25
Свойства куба.
1.Четыре сечения куба являются правильными шестиугольниками —
эти сечения проходят через центр куба перпендикулярно четырём его
главным диагоналям.2.В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все.шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба/
3.В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
4.Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
5.В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Слайд 26 Диагональю куба- называют отрезок, соединяющий две вершины, симметричные
относительно центра куба. Диагональ куба находится по формуле ,
где d — диагональ, а — ребро куба.Слайд 27 В свое время, в1919 году, Чарльз Форт сделал
предположение, которое могло бы объяснить происхождение странной находки, и
заключалось оно в том, что «зальцбургский параллелепипед» — это ископаемый артефакт, оставленный представителями иных миров, которые в глубокой древности посещали Землю. Уже в наше время была высказана гипотеза о том, что артефакт — дело рук человека.«Зальцбургский параллелепипед»