- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сечения фигур
Содержание
- 2. СодержаниеОпределение.Примеры построений сечений.Задания на построение сечений.
- 3. Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью
- 4. Сечение пирамид.Пирамида – это многогранник, одна из
- 5. Дано:АВСD – пирамидаТочка М принадлежит грани ABD.Построить сечение, проходящее через точку М // плоскости основание.
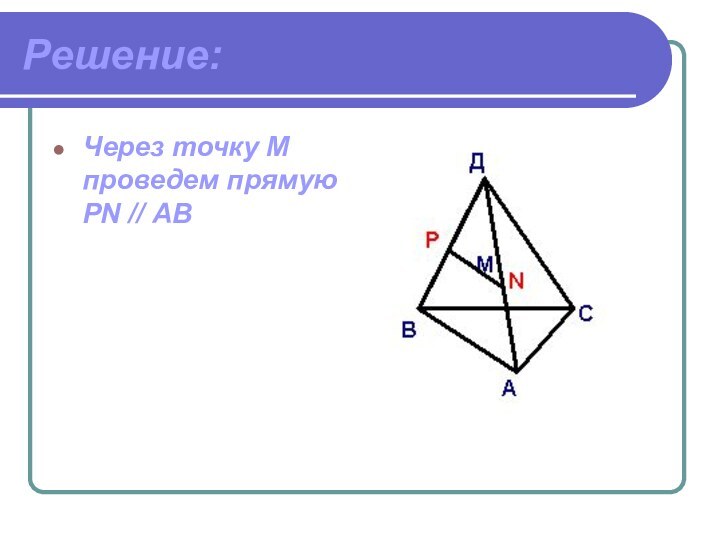
- 6. Решение:Через точку М проведем прямую PN // АВ
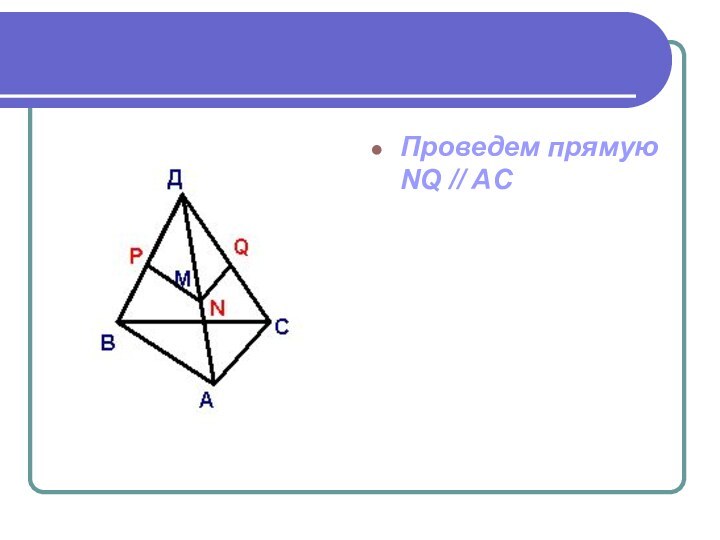
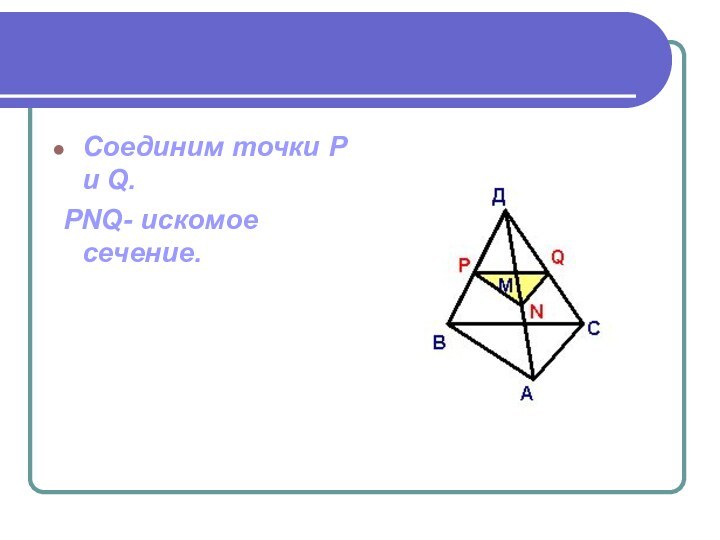
- 7. Проведем прямую NQ // AC
- 8. Соединим точки P и Q. PNQ- искомое сечение.
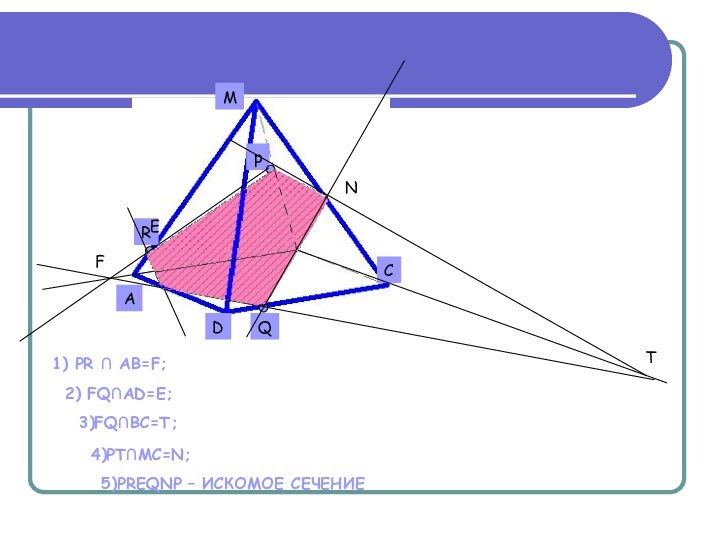
- 10. FT1) PR ∩ AB=F;2) FQ∩AD=E;3)FQ∩BC=T;4)PT∩MC=N;5)PREQNP – ИСКОМОЕ СЕЧЕНИЕЕN
- 11. Сечение кубаПрямоугольный параллелепипед, у которого все три
- 12. Дано: ABCDА1B1C1D1 -куб, точка
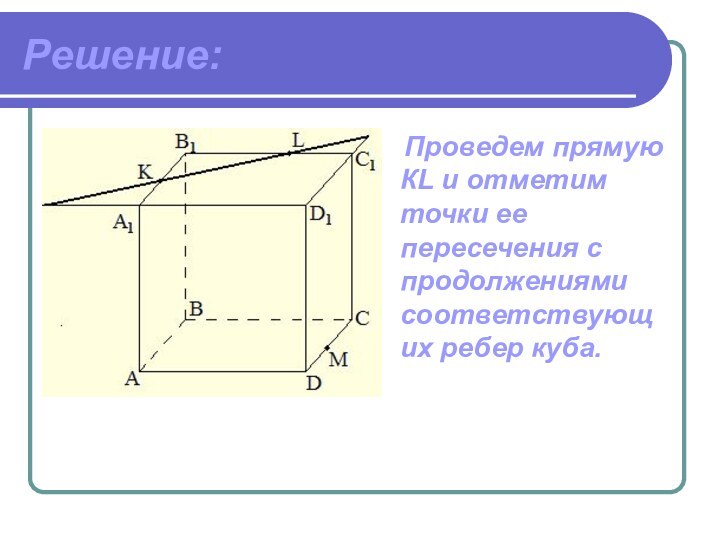
- 13. Решение: Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих ребер куба.
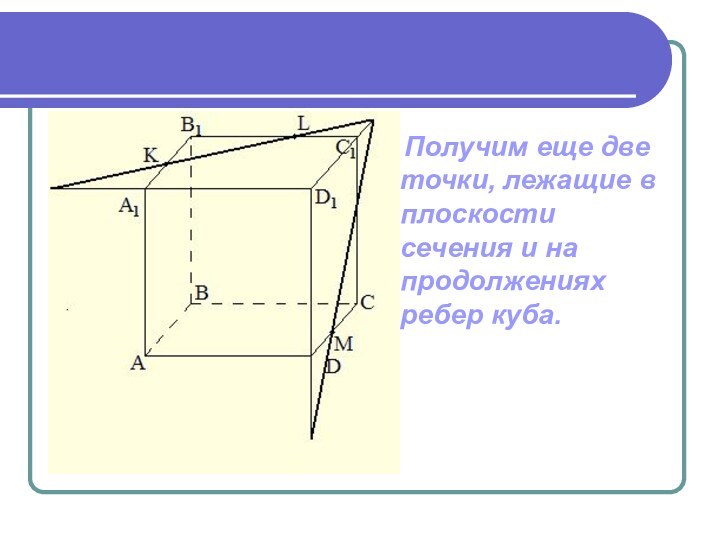
- 14. Получим еще две точки, лежащие в плоскости сечения и на продолжениях ребер куба.
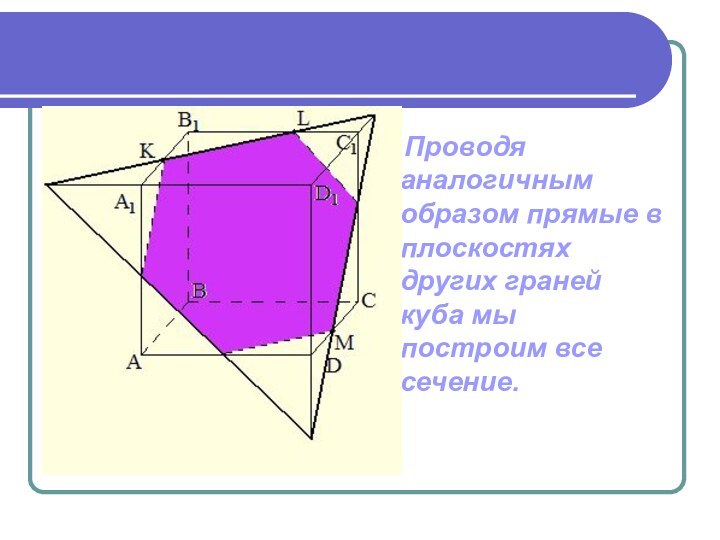
- 15. Проводя аналогичным образом прямые в плоскостях других граней куба мы построим все сечение.
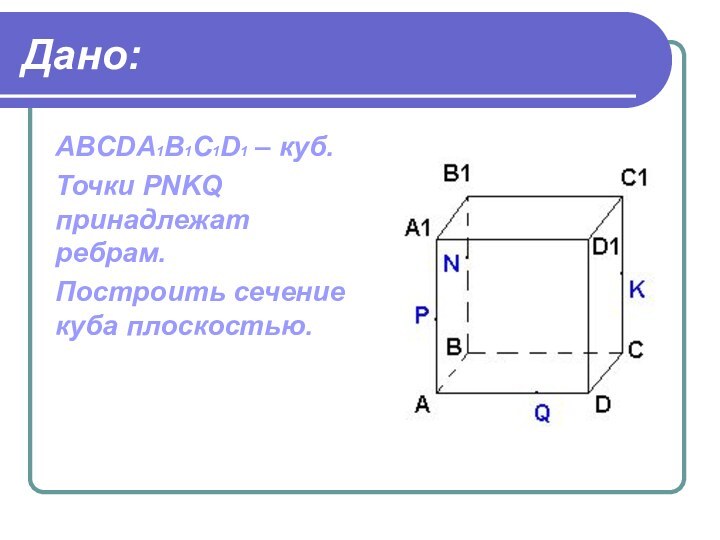
- 16. Дано:ABCDA1B1C1D1 – куб.Точки PNKQ принадлежат ребрам.Построить сечение куба плоскостью.
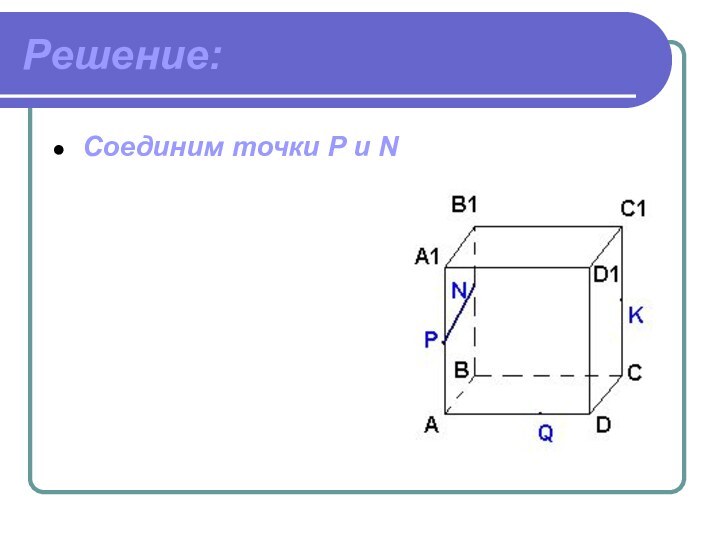
- 17. Решение:Соединим точки P и N
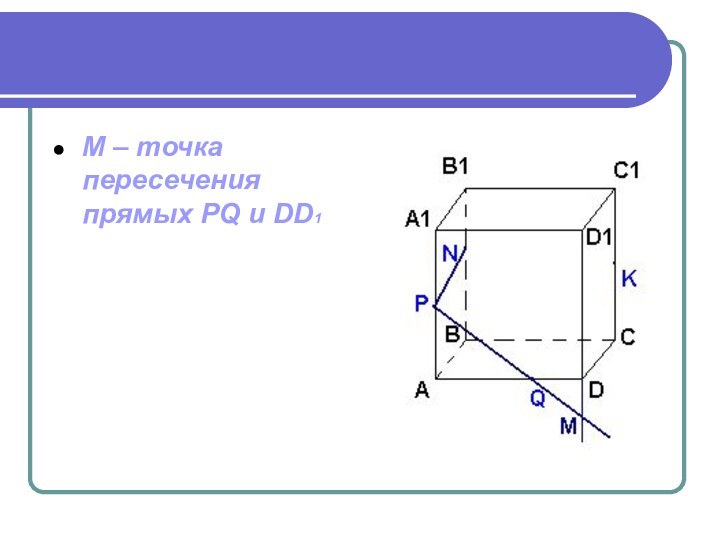
- 18. М – точка пересечения прямых PQ и DD1
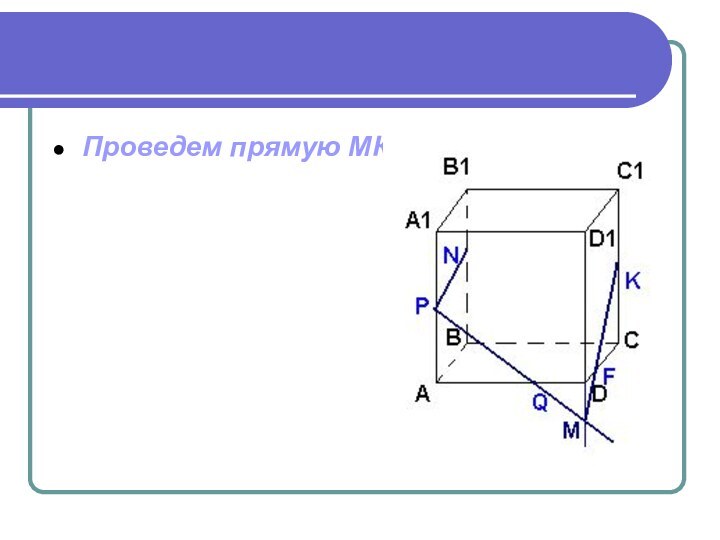
- 19. Проведем прямую МК
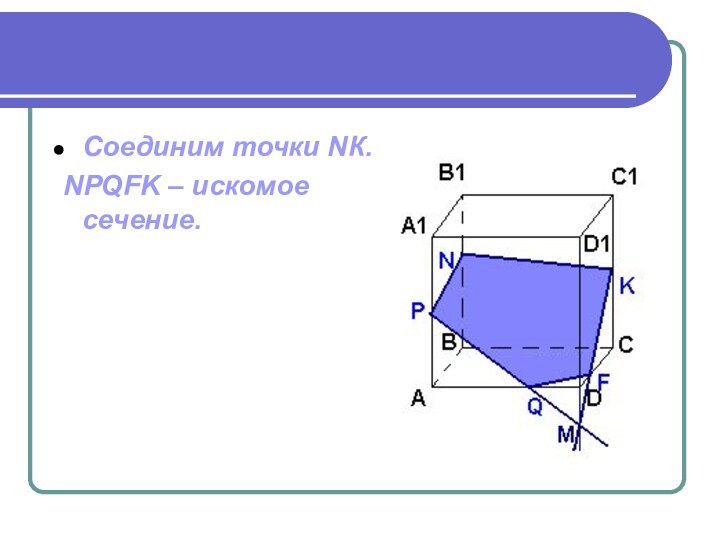
- 20. Соединим точки NК. NPQFK – искомое сечение.
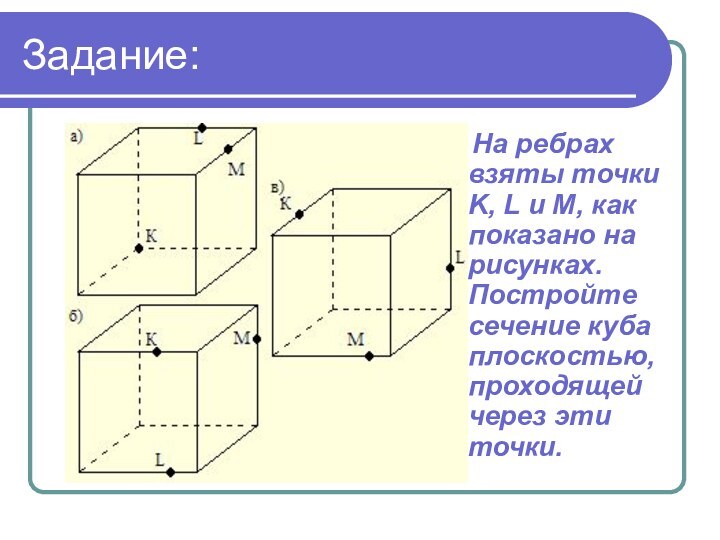
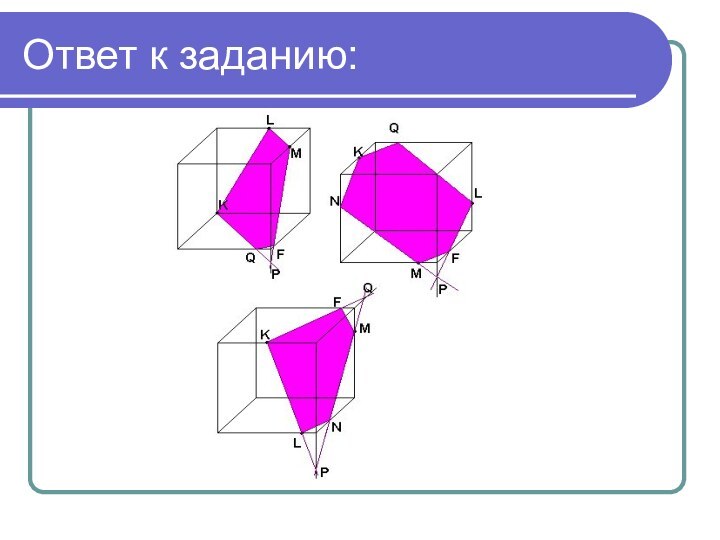
- 21. Задание: На ребрах взяты точки K,
- 22. Ответ к заданию:
- 23. Мир многогранников!
- 24. «Правильных многогранников вызывающе мало, но этот весьма
- 25. За каждым многогранником закреплено его значение, НАПРИМЕР:Тетраэдр является огнём!
- 26. куб-земля
- 27. октаэдр-воздух
- 28. Даже пчёлы знакомы с понятием многогранник!!!
- 29. Скачать презентацию
- 30. Похожие презентации
СодержаниеОпределение.Примеры построений сечений.Задания на построение сечений.











Слайд 3
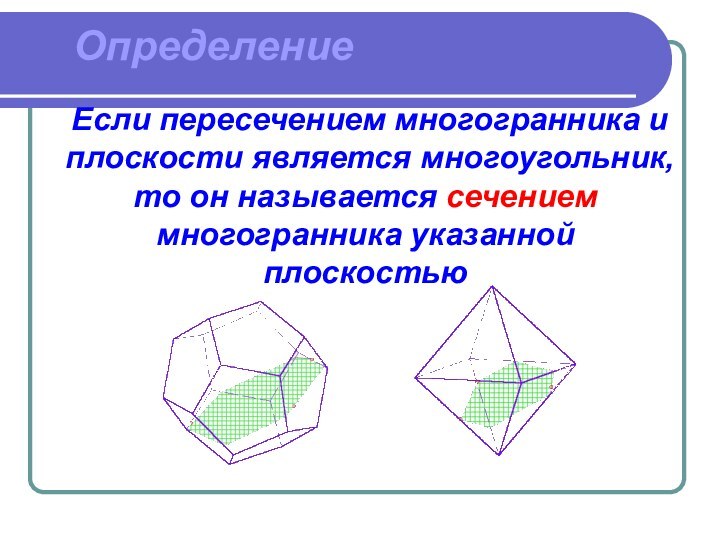
Определение
Если пересечением многогранника и плоскости является многоугольник, то
он называется сечением многогранника указанной плоскостью
Слайд 4
Сечение пирамид.
Пирамида – это многогранник, одна из граней
которого – произвольный многоугольник.
Тетраэдр - это многогранник, одна
из граней которого – произвольный треугольник.Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники.
Слайд 5
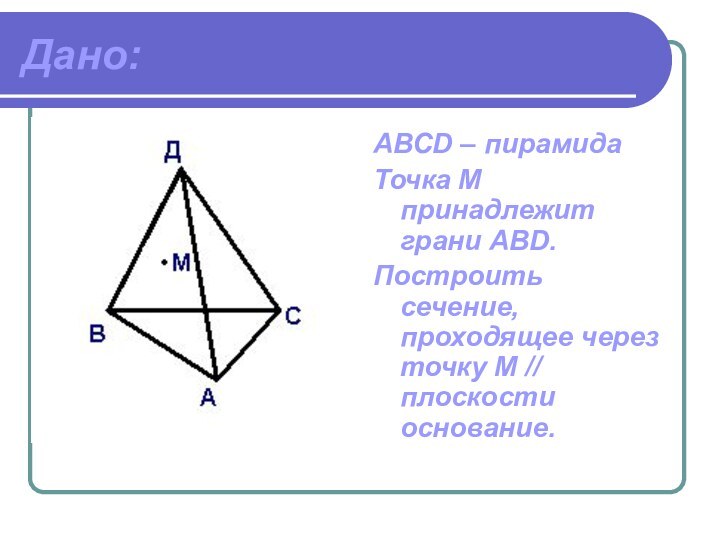
Дано:
АВСD – пирамида
Точка М принадлежит грани ABD.
Построить сечение,
проходящее через точку М // плоскости основание.
Слайд 9
Дано:
Пирамида MABCD. Постройте сечение пирамиды, проходящее через
точки P, Q, R. Известно, что точка P ∈ MB, точка R ∈ MA, Q ∈DC.ВАЖНО!
Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.
Слайд 11
Сечение куба
Прямоугольный параллелепипед, у которого все три измерения
равны, называется кубом.
Куб имеет 6 граней. Его сечениями
могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.
Слайд 12
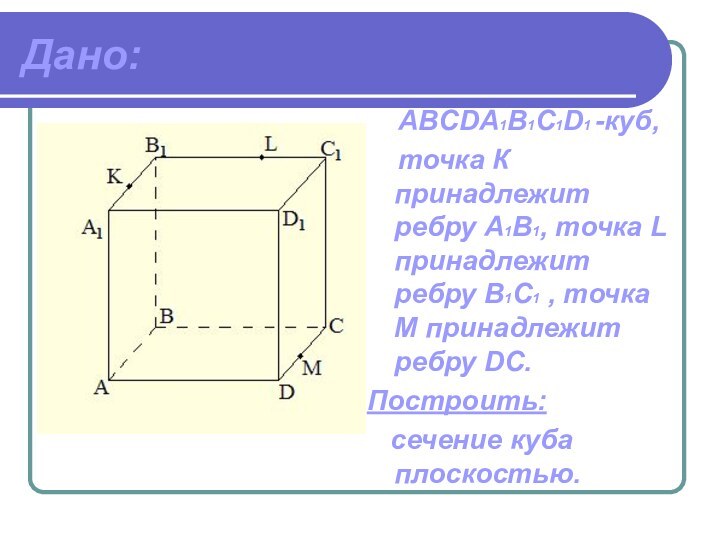
Дано:
ABCDА1B1C1D1 -куб,
точка К
принадлежит ребру A1В1, точка L принадлежит ребру В1C1
, точка М принадлежит ребру DC.Построить:
сечение куба плоскостью.