Презентация на тему Учебная презентация по теме Центральные и вписанные углы

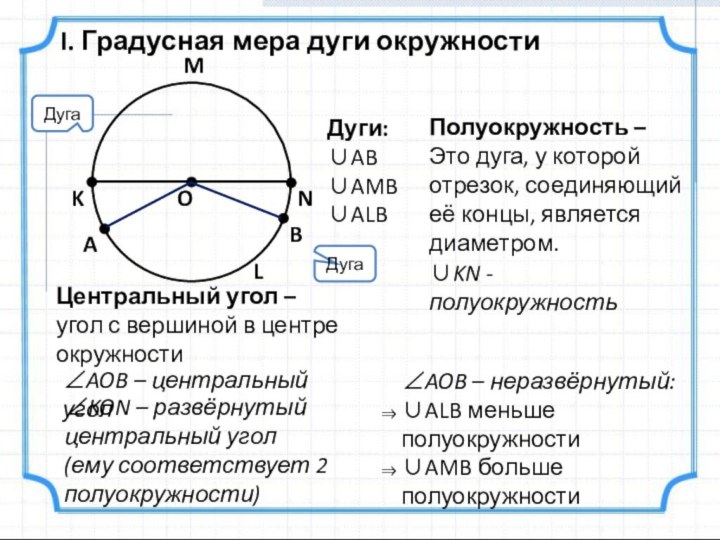
дуга, у которой отрезок, соединяющий её концы, является диаметром.
∪KN

Центральный угол –
угол с вершиной в центре окружности

∠AOB – центральный угол

∠KON – развёрнутый центральный угол
(ему соответствует 2 полуокружности)

∠AOB – неразвёрнутый:
∪ALB меньше полуокружности
∪AMB больше полуокружности

или является полуокружностью, то её градусная мера равна градусной

∪AMB = 360° - ∠АОВ
∪ALB = ∠АОВ

Сумма градусных мер двух дуг окружности с общими концами равна 360 °

окружности. Докажите, что если ∪AB = ∪CD, то AB

Дано:
ω (O, r),
A∈ω, B∈ω, C∈ω, D∈ω,
∪AB = ∪CD
Доказать:
AB = CD

Доказательство:
(∪AB = ∠AOB) ∧ (∪CD = ∠COD)
∪AB = ∪CD ⇒ ∠AOB = ∠COD
(AO = OD = OC = OB = r) ∧ (∠AOB = ∠COD) ⇒ ΔAOB = ΔCOD ⇒ AB = CD

ЧТД

лежит на окружности, а стороны её пересекают.
∠ABC – вписанный

на которую он опирается.
Дано: ω (O, r),
∠ABC – вписанный

Случаи расположения луча ВО относительно ∠ABC

1. Луч ВО совпадает с одной из сторон ∠ABC

А

С

В

О

Доказательство:
∪AC < полуокружности ⇒ ∠AOC = ∪AC
∠AOC – внешний угол ΔAOB ⇒ ∠AOC = ∠1 + ∠2
BO = OA = r ⇒ ΔAOB – равнобедренный ⇒ ∠1 = ∠2
П. 2, п. 3 ⇒ ∠AOC = 2⋅∠1 ⇒ ∠ABC = ½ ∪AC

2

1

ЧТД

на ∪AC
A∈ω, B∈ω, C∈ω
Доказать: ∠ABC = ½ ∪AC
2. Луч

Доказательство:
BO ∩ ∪AC = {D}
∠ABC = ∠ABD + ∠DBC
∠ABD = ½ ∪AD, ∠DBC = ½ ∪DC (Случай №1)
∠ABC = ½ ∪AD + ½ ∪DC ⇒ ∠ABC = ½ ∪AC

ЧТД

на ∪AC
A∈ω, B∈ω, C∈ω
Доказать: ∠ABC = ½ ∪AC
3. Луч

Доказательство:
BO ∩ ∪AC = {D}
∠ABC = ∠ABD - ∠DBC
∠ABD = ½ ∪AD, ∠DBC = ½ ∪DC (Случай №1)
∠ABC = ½ ∪AD - ½ ∪DC ⇒ ∠ABC = ½ ∪AC

ЧТД

же дугу, равны
Следствие 2.
Вписанный угол, опирающийся на полуокружность, -

105 °
х = 50 °

окружности пересекаются, то произведение отрезков одной хорды равно произведению

1

Дано: ω (O, r),
A∈ω, B∈ω, C∈ω, D∈ω,
AB ∩ CD = {E}
Доказать:
AE⋅BE = CE⋅DE

Доказательство:

2

3

4

∠1 и ∠2 опираются на ∪DB , ∠1 = ∠2 (Следствие 1)
∠3 = ∠4 (Как вертикальные)
П.1, п.2 ⇒ ΔADE ~ ΔCBE (1 ППТ) ⇒

ЧТД

а хорда АС – дугу в 43°. Найдите угол

Решение:
∠BAC = ½ ∪BC
C1 ∈ ∪ALB ∪BC1 = 360° - ∪AC1 - ∪AB = 360° - 43° - 115° = 202° ∠BAC1 = ½ ⋅ 202° = 101°
C2 ∉ ∪ALB ∪BC2 = ∪AB - ∪AC2 - = 115° - 43° = 72° ∠BAC2 = ½ ⋅ 72° = 36°

Ответ: 101°, 36°

АВ (В – точка касания) и секущая AD, проходящая

Решение:
∪BD = ∠BOD = 110°20′
∠ABO = 90° ⇒ ∠BAD = ∠BOD - 90° = 20°20′ (т.к. ∠BOD внешний угол ΔABO)
BO = OD = r ⇒ ΔBOD – равнобедренный ⇒ ∠OBD = ∠BDO = ∠ADB ⇒ ∠ADB = (180° - ∠BOD) / 2 = 34°50′

Ответ: 20°20′, 34°50′

точки, лежащей вне окружности, если дуги, заключенные между секущими,

Решение:
½ ∪BC = ∠BAC = 70°
½ ∪AD = ∠ACD = 26°
∠BAC внешний угол ΔOAC ⇒ ∠AOD = ∠BAC - ∠OCA ⇒ ∠AOD = 70° - 26° = 44°


Ответ: 44°

Найдите ED, если:
А) АЕ =5, BE = 2, CE

Дано: ω (O, r),
AB ∩ CD = {E}
Найти: ED
Решение:
AE⋅BE = CE⋅DE (по теореме о пересекающихся хордах) ⇒

к диаметру, есть среднее пропорциональное для отрезков, на которые

Доказательство:
∠ACB вписанный и опирается на полуокружность ⇒
∠ACB = 90° ⇒

ЧТД