Презентация на тему Ориентация поверхности

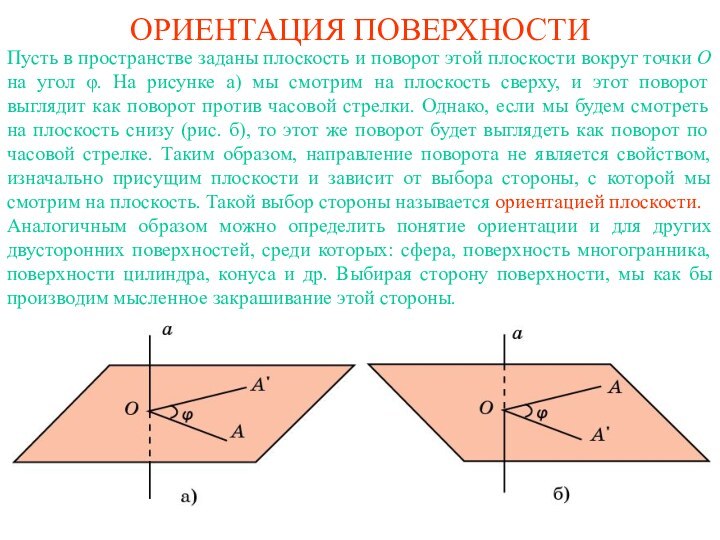
не для любой поверхности. Первым примером такой неориентируемой поверхности

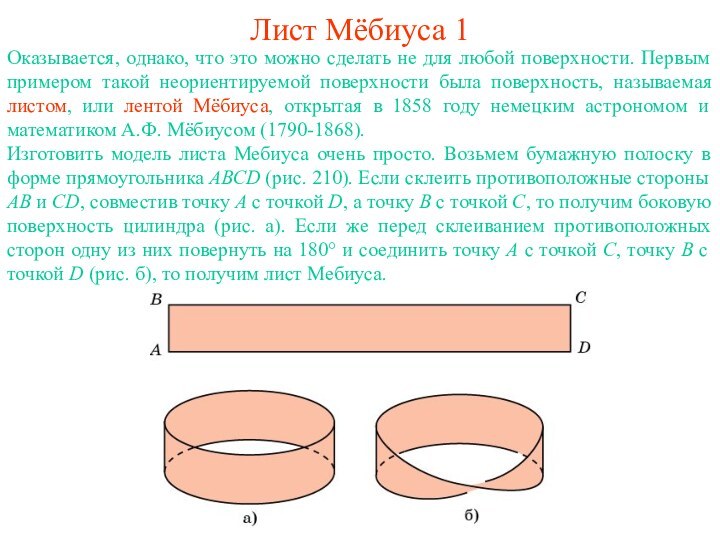
была поверхность, называемая листом, или лентой Мёбиуса, открытая в 1858 году немецким астрономом и математиком А.Ф. Мёбиусом (1790-1868).

Изготовить модель листа Мебиуса очень просто. Возьмем бумажную полоску в форме прямоугольника АВСD (рис. 210). Если склеить противоположные стороны АВ и CD, совместив точку А с точкой D, а точку В с точкой С, то получим боковую поверхность цилиндра (рис. а). Если же перед склеиванием противоположных сторон одну из них повернуть на 180° и соединить точку A с точкой C, точку B с точкой D (рис. б), то получим лист Мебиуса.

Муравью, ползущему по листу Мебиуса, не надо переползать через

его край, чтобы попасть на противоположную сторону, как это видно на гравюре М. Эшера.
Свойство односторонности листа Мебиуса используется при изготовлении ременных передач. Если ремень сделать в виде ленты Мебиуса, то он будет изнашиваться вдвое медленнее, чем обычный. Это объясняется тем, что в работе ремня, изготовленного в виде ленты Мебиуса, принимает участие вся поверхность, а не только внутренняя ее часть, как у обычной ременной передачи.

поверхность цилиндра; в) поверхность конуса?
Ответ: а) Да;
б) да;
в) да.

полученная вращением окружности вокруг прямой, лежащей в плоскости окружности

и не пересекающей эту окружность)?

Ответ: Две.

лента; б) трижды перекрученная лента?
Ответ: а) Да;
б) нет.

г).

Нет.

листа Мебиуса по средней линии?
Ответ: Две.

по средней линии?
Ответ: Две сцепленные дважды перекрученные ленты.

по средней линии, а отступив от края на треть

ширины ленты?

Ответ: Сцепленные лист Мебиуса и четырежды перекрученная лента.

этой прямой и одновременно вращается вокруг своего центра в

плоскости отрезка AB и прямой a. За время полного оборота вокруг прямой a отрезок совершает поворот на 180° вокруг своего центра?

эластичного материала. Вырежем в ней круглое отверстие (рис. а),

проденем в него один конец цилиндра и склеим окружности оснований. Получившаяся поверхность изображена на рисунке б (бутылка Клейна). Сколько у нее сторон?

Ответ: Одна.

к их краям приклеили основания боковой поверхности цилиндра (рис.

а, б). Сколько сторон имеет образовавшаяся поверхность?

Ответ: а) Две;

б) одну.