- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Треугольник
Содержание
- 2. Содержание:1) Давайте вспомним.2)Подобные фигуры3)Определение подобных треугольников4)Признаки подобия треугольника5) Это интересно.6) Еще немного о треугольниках.
- 3. Давайте вспомним Треугольник- это геометрическая фигура состоящая
- 4. Подобные фигурыЧем похожи фигуры?ФОРМОЙ!
- 5. Определение подобных треугольников Два треугольника называются подобными,
- 6. Признаки подобия треугольников 1 Если два угла
- 7. Углы соответственно равныАВСВ1А1С1
- 8. Сходственные стороны ВАСВ1А1С1пропорциональны
- 9. АВСА1В1С1ЕСЛИА= А1 В= В1 С= С1АВСА1В1С1Коэффициент подобия “k”
- 10. Назовите сходственные стороны.АСВМКРРавенство отношений сходственных сторон.
- 11. Какие треугольники подобны?14235
- 12. Окружности- всегда подобны Квадраты- всегда подобны
- 13. Очень интересноПо легенде Фалес измерил высоту одной
- 14. Еще немного о треугольниках.
- 15. Пропорциональные отрезки в треугольнике Биссектриса любого внутреннего
- 16. Высота треугольника Высотой треугольника называется перпендикуляр,
- 17. Медиана треугольника Медианой треугольника
- 18. Биссектриса Биссектрисой треугольника называется отрезок биссектрисы
- 19. Скачать презентацию
- 20. Похожие презентации
Содержание:1) Давайте вспомним.2)Подобные фигуры3)Определение подобных треугольников4)Признаки подобия треугольника5) Это интересно.6) Еще немного о треугольниках.


















Слайд 2
Содержание:
1) Давайте вспомним.
2)Подобные фигуры
3)Определение подобных треугольников
4)Признаки подобия треугольника
5)
Это интересно.
Слайд 3
Давайте вспомним
Треугольник- это геометрическая фигура состоящая из
трех точек не лежащие на прямой и трех отрезков,
попарно соединяющих эти точки. Эти точки называются вершинами треугольника, а отрезки сторонами треугольника.
Слайд 5
Определение подобных треугольников
Два треугольника называются подобными, если
их углы соответственно равны и стороны одного треугольника пропорциональны
сходственным сторонам другого.
Слайд 6
Признаки подобия треугольников
1 Если два угла одного
треугольника соответственно равны двум углам другого, то такие треугольники
подобны.2 Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3 Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Слайд 13
Очень интересно
По легенде Фалес измерил высоту одной из
Египетских пирамид,
используя метод подобия треугольников
200
6
4
А
В
С
А1
В1
С1
Тень от пирамиды
Тень от палки
Высота
шеста - 4 локтя
Длина тени шеста - 6 локтей
Длина тени пирамиды - 200 локтей[приблизительно 133,3 локтя (133 1/3)]
Слайд 15
Пропорциональные отрезки в треугольнике
Биссектриса любого внутреннего угла
треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:
Слайд 16
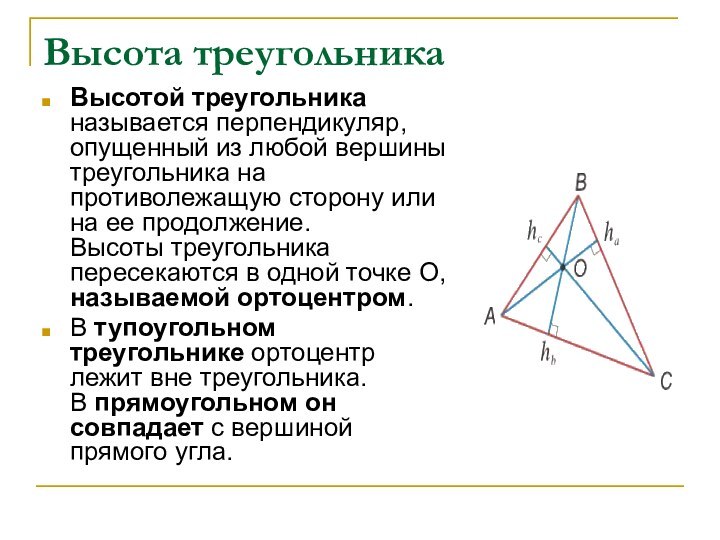
Высота треугольника
Высотой треугольника
называется перпендикуляр, опущенный из
любой вершины треугольника на противолежащую сторону или на ее
продолжение. Высоты треугольника пересекаются в одной точке О, называемой ортоцентром.В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном он совпадает с вершиной прямого угла.
Слайд 17
Медиана треугольника
Медианой треугольника
называется отрезок, соединяющий любую
вершину треугольника с серединой противоположной стороны. Медианы треугольника пересекаются в
одной точке О, являющейся центром тяжести треугольника. Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).
Слайд 18
Биссектриса
Биссектрисой треугольника
называется отрезок биссектрисы любого угла
от вершины до пересечения с противоположной стороной.
Биссектрисой угла называется
луч, делящий угол пополам. Биссектрисы треугольника пересекаются в одной точке, являющейся центром вписанной окружности.