Презентация на тему Учебная презентация по теме Системы логических уравнений (СЛУ)

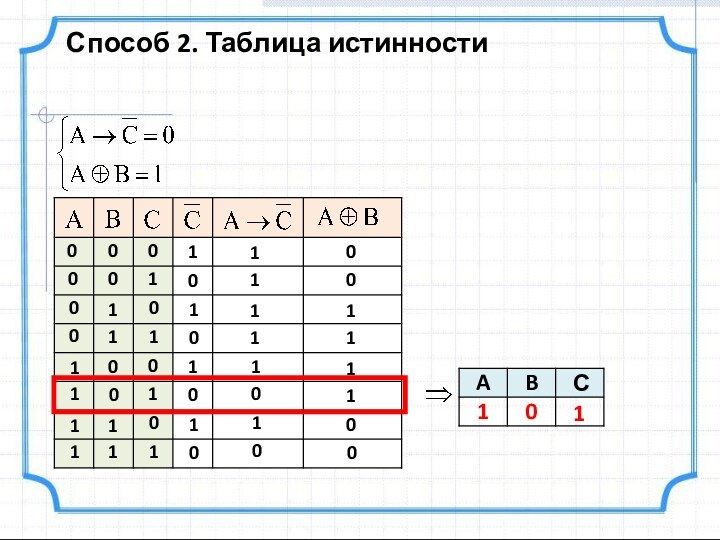
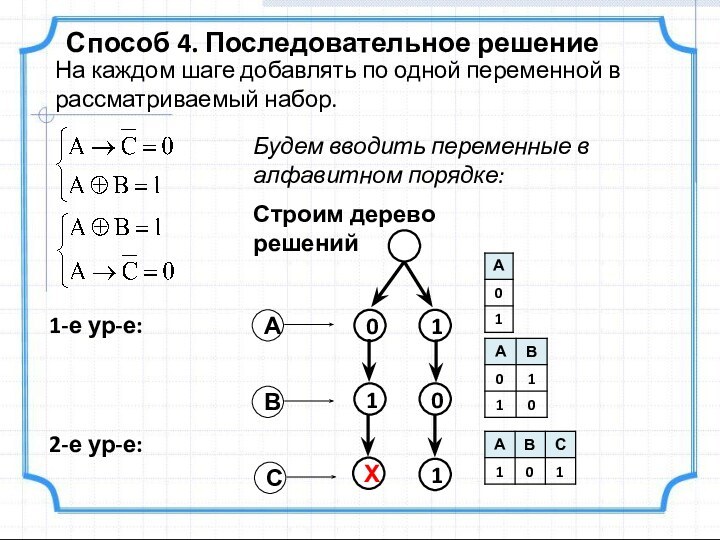
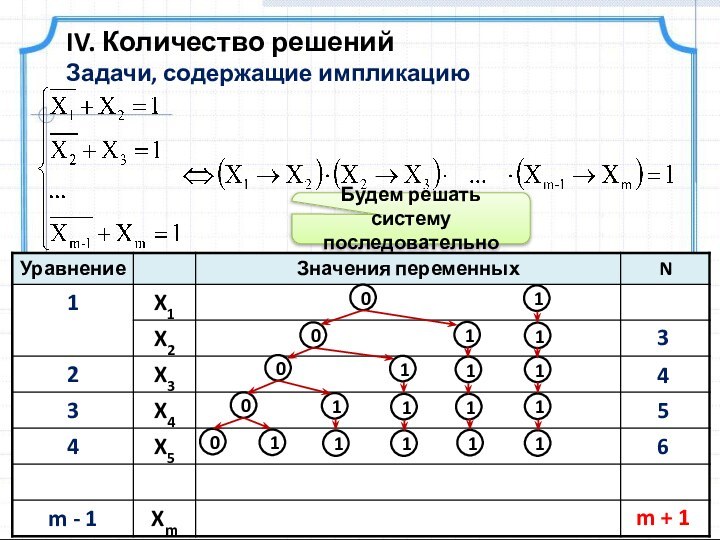
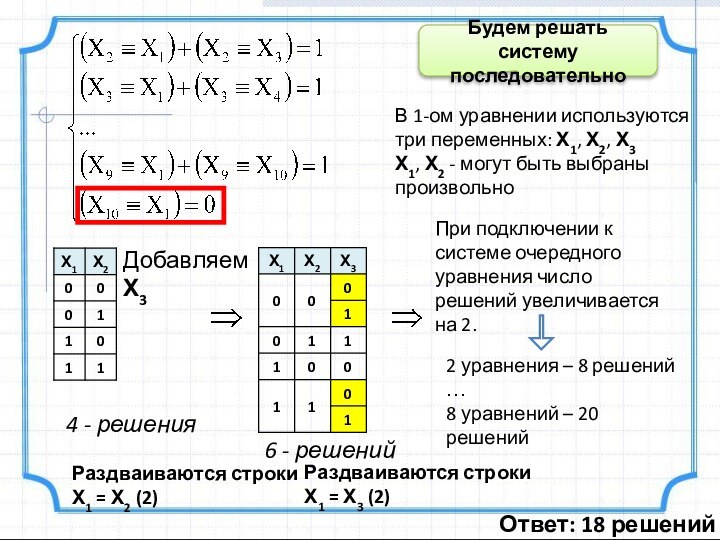
истинны:
1) Неверно, что если корабль A вышел в море,

Решение:
Обозначим буквами высказывания:
A — “корабль A вышел в море”,
B — “корабль B вышел в море”,
C — “корабль C вышел в море”.

Найти значения A, B и C, при которых оба
уравнения превращаются в истинные
равенства.

вышли корабли А и С

ее равной 0 или 1)
Упростить уравнения
Зафиксировать значение второй переменной

1) A = 0

Решений не имеет
(т.к. 1→0=0)

2) A = 1

C=1

B=0

1

A

B

0

С

1

Ответ: В море вышли корабли А и С

одной переменной в рассматриваемый набор.
Будем вводить переменные в алфавитном

Строим дерево решений

0

1

1-е ур-е:

2-е ур-е:

Х

1

и Y = C → D
Тогда уравнение принимает вид:

Ответ: 3+3+9=15

Сколько решений имеет уравнение

A → B = 0
1 решение: (1,0)

C → D = 1
3 решения:
(0,1), (0,0), (1,1)

Всего решений: 1·3=3

A → B = 1
3 решения:
(0,1), (0,0), (1,1)

C → D = 0
1 решение: (1,0)

Всего решений: 1·3=3

A → B = 1
C → D = 1
Каждое уравнение имеет по 3 решения:
(0,1), (0,0), (1,1)

Всего решений: 3·3=9

В данном случае не самый рациональный подход

уравнение имеет 24 – 1 = 15 решений

Решение:
Проведем замену переменных
СЛУ имеет 11 решений
(см. предыдущую задачу)
Ответ: 11

зависят друг от друга
⇒
Их можно решать отдельно
Имеет 6

Имеет 6 решений

Общее количество решений:
6·6=36

Ответ: 36

переменных: Х1, Х2, Х3
Х1, Х2 - могут быть выбраны

Добавляем
Х3

4 - решения

6 - решений

Раздваиваются строки
Х1 = Х2 (2)

Раздваиваются строки
Х1 = Х3 (2)

При подключении к системе очередного уравнения число решений увеличивается на 2.

2 уравнения – 8 решений
…
8 уравнений – 20 решений

Ответ: 18 решений