Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по информатике на тему Основы логики(10 класс)

Содержание

2. Алгебра логики (булева алгебра) - это раздел
3. Джордж Буль
4. Логическое высказывание — это любое повествовательное предложение,
5. Пример: «Трава зеленая» -истинное высказывание. «Лев – птица» - ложное высказывание.
6. Не всякое предложение является логическим высказыванием.
7. Употребляемые в обычной речи слова и словосочетания
8. Высказывания, образованные из других высказываний с помощью
9. Пример: Элементарные высказывания: «Петров — врач», «Петров
10. Чтобы обращаться к логическим высказываниям, их обозначают
11. Пример:А ="Тимур поедет летом на море", В
12. Операции над логическими высказываниями
13. Таблица истинности это табличное представление логической схемы
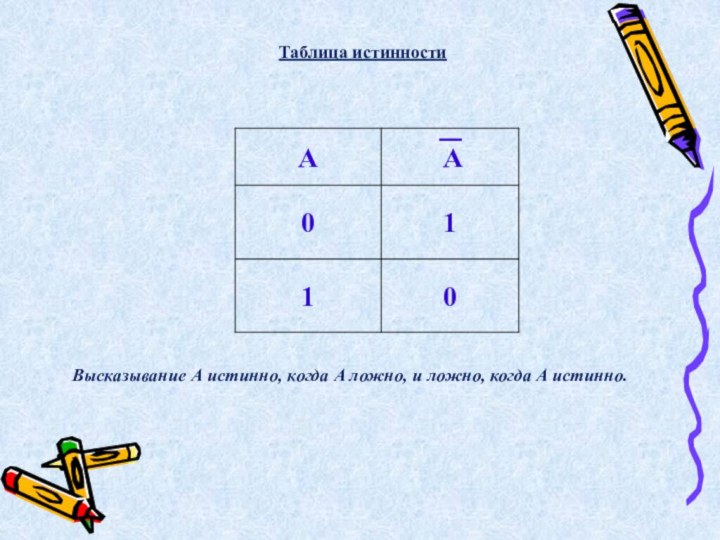
14. Логическое «отрицание» (инверсия или НЕ) обозначается чертой над высказыванием Ā .
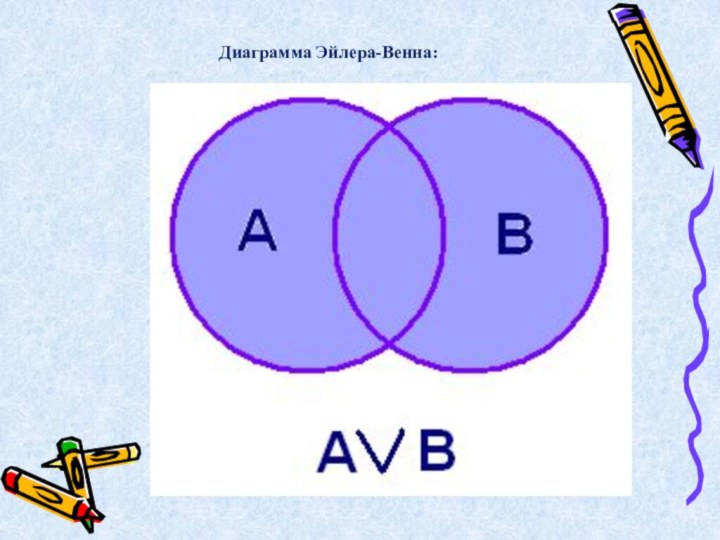
15. Диаграмма Эйлера-Венна:
16. Пример:А = «Луна — спутник Земли»А = "Луна — не спутник Земли"
17. Высказывание А истинно, когда A ложно, и ложно, когда A истинно. Таблица истинности
18. Логическое умножение ( «и», конъюнкция
19. Диаграмма Эйлера-Венна:
20. Пример: А = «10 делится на 2»,
21. Высказывание А · В истинно тогда и
22. Логическое сложение ( «или», дизъюнкция (лат.
23. Диаграмма Эйлера-Венна:
24. Высказывание А v В ложно тогда и
25. Импликация (лат. implico — тесно связаны)
26. Высказывание А В
27. Эквиваленция (двойная импликация) - операция, выражаемая
28. Высказывание А В истинно
29. А = «10 делится на 2», А=
30. Порядок выполнения логических операций 1.Сначала выполняется операция
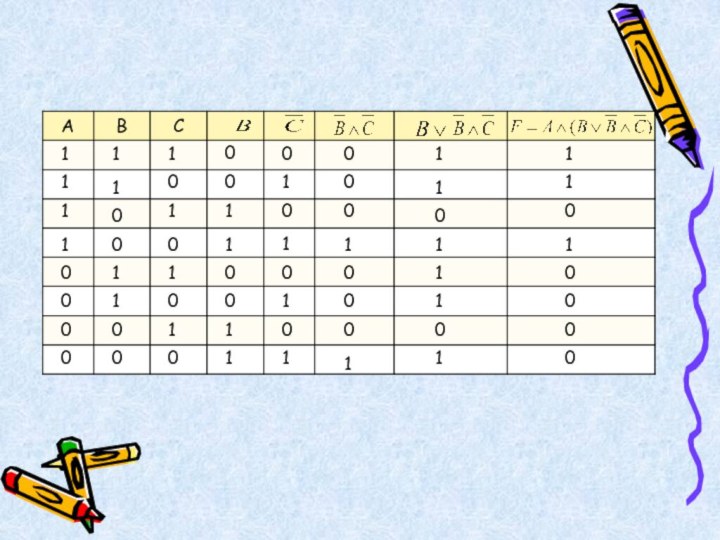
31. Задание 1.Построить таблицу истинности для логической функции
32. Алгоритм решения задачи:1. Определить количество строк в таблице истинности,
33. 1111111111110000000000000000000011111111000000111111110011100000
34. Построить таблицы истинности для следующих функций:
35. Скачать презентацию
36. Похожие презентации

Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Главная
Информатика
Презентация по информатике на тему Основы логики(10 класс)

Презентация«Основы логики» Урок по информатике для 10 класса

Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно

Пример: «Трава зеленая» -истинное высказывание. «Лев – птица» - ложное высказывание.

Не всякое предложение является логическим высказыванием. Пример: «ученик

Употребляемые в обычной речи слова и словосочетания

Высказывания, образованные из других высказываний с помощью логических связок, называются составными.

Пример: Элементарные высказывания: «Петров — врач», «Петров — шахматист» Составные высказывания:

Чтобы обращаться к логическим высказываниям, их обозначают буквами. Пример:А = «Луна –

Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все

Логическое «отрицание» (инверсия или НЕ) обозначается чертой над высказыванием Ā .

Высказывание А истинно, когда A ложно, и ложно, когда A истинно. Таблица истинности

Логическое умножение ( «и», конъюнкция (лат. conjunctio — соединение)) обозначается

Пример: А = «10 делится на 2», А= 1В = «5 больше

Высказывание А · В истинно тогда и только тогда, когда оба высказывания

Логическое сложение ( «или», дизъюнкция (лат. disjunctio — разделение) обозначается знаком

Высказывание А v В ложно тогда и только тогда, когда оба высказывания

Импликация (лат. implico — тесно связаны) -операция, выражаемая связками «если

Высказывание А В ложно тогда и только тогда,

Эквиваленция (двойная импликация) - операция, выражаемая связками «тогда и только тогда»,

Высказывание А В истинно тогда и только тогда, когда

А = «10 делится на 2», А= 1В = «5 больше 3»,

Порядок выполнения логических операций 1.Сначала выполняется операция отрицания (“не”), 2. Затем конъюнкция

Задание 1.Построить таблицу истинности для логической функции

Алгоритм решения задачи:1. Определить количество строк в таблице истинности, которое равно количеству возможных комбинаций

1111111111110000000000000000000011111111000000111111110011100000

Построить таблицы истинности для следующих функций:

Слайды презентации

Слайд 2 Алгебра логики (булева алгебра) - это раздел математики,

Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые

изучающий высказывания, рассматриваемые со стороны их логических значений (истинности

или ложности) и логических операций над ними.

Слайд 3 Джордж Буль

Слайд 4 Логическое высказывание — это любое повествовательное предложение, в

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно

отношении которого можно однозначно сказать, истинно оно или ложно.

Слайд 5 Пример:

«Трава зеленая» -истинное высказывание.

«Лев – птица»

- ложное высказывание.

Слайд 6 Не всякое предложение является логическим высказыванием. Пример: «ученик

Не всякое предложение является логическим высказыванием. Пример: «ученик десятого

десятого класса» «информатика — интересный предмет».

Слайд 7 Употребляемые в обычной речи слова и словосочетания "не",

"и", "или", "если... , то", "тогда и только тогда"

и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.

Слайд 8 Высказывания, образованные из других высказываний с помощью логических

связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.

Слайд 9 Пример:
Элементарные высказывания:
«Петров — врач»,
«Петров —

шахматист»
Составные высказывания:
"Петров — врач и шахматист", понимаемое

как "Петров — врач, хорошо играющий в шахматы".
"Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".

Слайд 10 Чтобы обращаться к логическим высказываниям, их обозначают буквами.

Пример:
А = «Луна – спутник Земли», А = 1
В

= « 3* 2 = 5», В = 0

Слайд 11 Пример:
А ="Тимур поедет летом на море",
В =

"Тимур летом отправится в горы".
А и В =

"Тимур летом побывает и на море, и в горах»

Слайд 12 Операции над логическими
высказываниями

Слайд 13 Таблица истинности это табличное представление логической схемы (операции),

Таблица истинности это табличное представление логической схемы (операции), в котором перечислены

в котором перечислены все возможные сочетания значений истинности входных

сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

Слайд 14 Логическое «отрицание»
(инверсия или НЕ) обозначается чертой

над высказыванием Ā .

Слайд 15 Диаграмма Эйлера-Венна:

Слайд 16
Пример:
А = «Луна — спутник Земли»
А = "Луна

— не спутник Земли"

Слайд 17 Высказывание А истинно, когда A ложно, и ложно,

когда A истинно.
Таблица истинности

Слайд 18 Логическое умножение
( «и», конъюнкция (лат.

Логическое умножение ( «и», конъюнкция (лат. conjunctio — соединение))

conjunctio — соединение)) обозначается точкой " . " (может

также обозначаться знаками /\ или &).
А . В, А /\ В, А & В

Слайд 19 Диаграмма Эйлера-Венна:

Слайд 20 Пример:
А = «10 делится на 2», А=

Пример: А = «10 делится на 2», А= 1В = «5

1
В = «5 больше 3», В = 1
С =

« 4 – нечётное число», С = 0
А & В = «10 делится на 2 и 5 больше 3», А & В = 1
А & С = «10 делится на 2 и 4 – нечётное число», А & С = 0

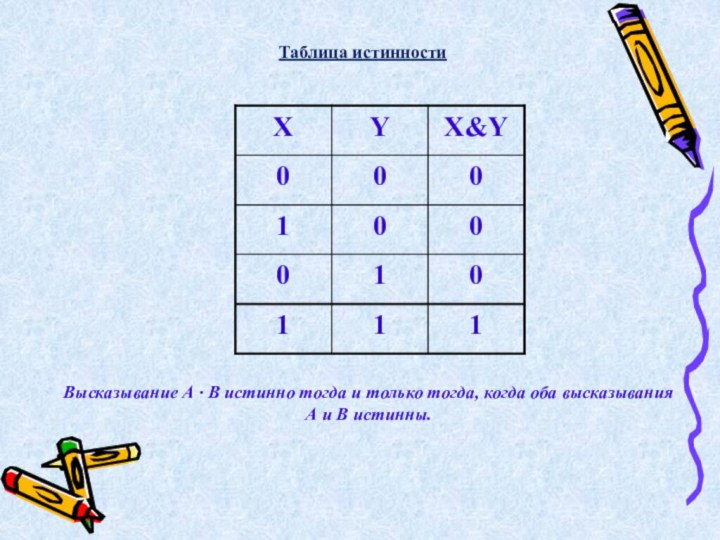
Слайд 21 Высказывание А · В истинно тогда и только

Высказывание А · В истинно тогда и только тогда, когда оба

тогда, когда оба высказывания А и В истинны.
Таблица

истинности

Слайд 22 Логическое сложение
( «или», дизъюнкция (лат. disjunctio

Логическое сложение ( «или», дизъюнкция (лат. disjunctio — разделение) обозначается

— разделение) обозначается знаком v или +.
А V

В, А + В

Слайд 23 Диаграмма Эйлера-Венна:

Слайд 24 Высказывание А v В ложно тогда и только

Высказывание А v В ложно тогда и только тогда, когда оба

тогда, когда оба высказывания А и В ложны.
Таблица истинности

Слайд 25 Импликация (лат. implico — тесно связаны)
-операция,

Импликация (лат. implico — тесно связаны) -операция, выражаемая связками

выражаемая связками «если ..., то…», «из ... следует…»,

«... влечет ...».
Обозначается знаком .
А В

.

Слайд 26 Высказывание А В ложно

тогда и только тогда, когда А истинно, а В

– ложно.

Таблица истинности

Слайд 27 Эквиваленция (двойная импликация)

- операция, выражаемая связками

Эквиваленция (двойная импликация) - операция, выражаемая связками «тогда и только

«тогда и только тогда», «необходимо и достаточно», «... равносильно

...» Обозначается знаком или ~.
А В, А ~ В.

Слайд 28 Высказывание А В истинно тогда

Высказывание А В истинно тогда и только тогда, когда значения

и только тогда, когда значения А и В совпадают.

Таблица истинности

Слайд 29 А = «10 делится на 2», А= 1
В

А = «10 делится на 2», А= 1В = «5 больше

= «5 больше 3», В = 1
С = «

4 – нечётное число», С = 0
К = « 3 – чётное число», К = 0
А + В = «10 делится на 2 или 5 больше 3», А + В = 1
А + С = «10 делится на 2 или 4 – чётное число», А + С = 1
С + К = « 4 – нечётное число или 3 – чётное число», С+К = 0

Пример:

Слайд 30 Порядок выполнения логических операций

1.Сначала выполняется операция отрицания

Порядок выполнения логических операций 1.Сначала выполняется операция отрицания (“не”), 2. Затем

(“не”),
2. Затем конъюнкция (“и”),
3. После конъюнкции —

дизъюнкция (“или”),
4. В последнюю очередь — импликация и эквиваленция.

Слайд 31 Задание 1.
Построить таблицу истинности для логической функции

Слайд 32 Алгоритм решения задачи:
1. Определить количество строк в таблице истинности, которое

Алгоритм решения задачи:1. Определить количество строк в таблице истинности, которое равно количеству возможных

равно количеству возможных комбинаций значений логических переменных, входящих в

логическое выражение: количество строк = , где n – количество переменных
(Количество логических переменных – 3 (A, B, C) поэтому количество строк – = 8+1 (для названия столбцов)
2.Определить количество столбцов в таблице истинности, которое равно сумме количества операций m в логическом выражении и n количества переменных, т.е. (m+n) (в нашем случае m=5, n=3, поэтлму количество столбцов – 8)