Презентация на тему по информатике на тему ЕГЭ-2015

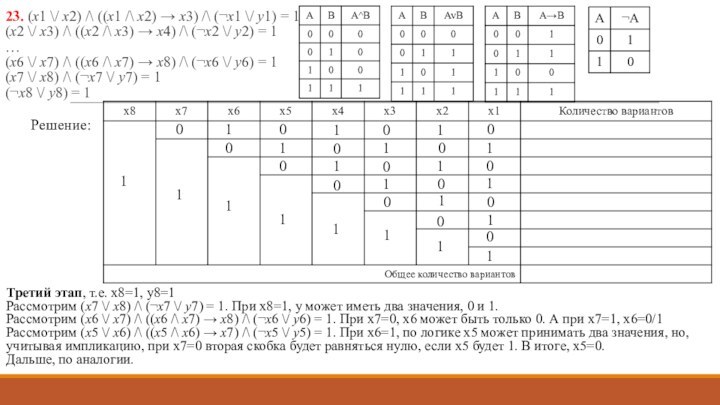
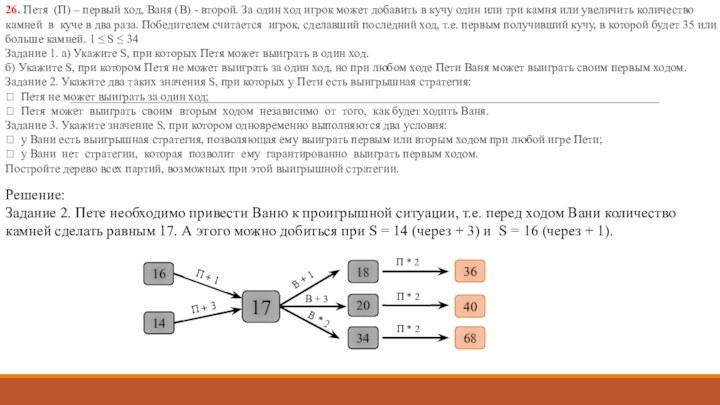
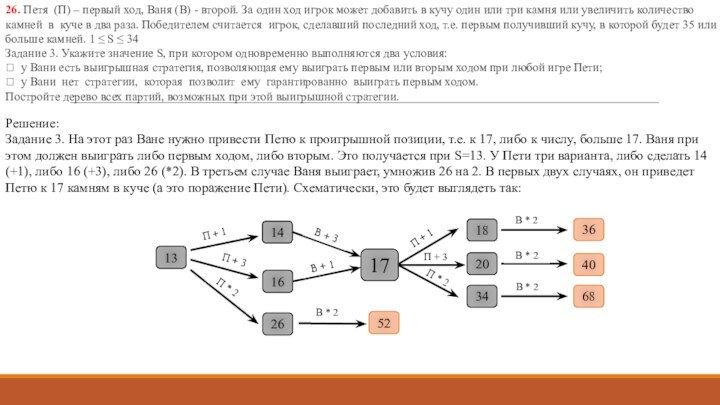
А, Б, В, Г и Д, используется неравномерный двоичный

код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать? 1) для буквы В – 101 2) это невозможно 3) для буквы В – 010 4) для буквы Б – 10

Решение:
А Б В Г Д
0 100 1010 111 110
1) После сокращения В с 1010 до 101, получим
А Б В Г Д
0 100 101 111 110
Декодирование по прежнему производится однозначно
2) Если первый вариант верный, то второй автоматический отпадает.
3) А Б В Г Д
0 100 010 111 110
или В А В Г Д
010 0 010 111 110
Два варианта декодирования.

4) А Б В Г Д
0 10 1010 111 110
или А Б Б Б Г Д
0 10 10 10 111 110
Два варианта декодирования.

Ответ: 1

Она успела заполнить лишь небольшой фрагмент таблицы: Каким выражением может

быть F? 1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8 2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8 3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8 4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8

Решение:
Учитывая знаки отрицания, проверим каждый пример
1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8
1 0 = 0
1 1 = 1 или 0 (если будет среди примеров 0)
0 0 = 0 - не подходит
2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
0 0 = 0 или 1 (если будет среди примеров 1)
1 1 = 1
0 0 = 0 или 1 (если будет среди примеров 1) – подходит
3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8
0 1 = 0
0 0 = 0 - не подходит
4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
1 0 = 1- не подходит

Ответ: 2

имён файлов. Маска представляет собой последовательность букв, цифр и

прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы. Символ «?» (вопросительный знак) означает ровно один произвольный символ. Символ «*» (звёздочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность. В каталоге находится 7 файлов: carga.mp3 cascad.mpeg cassa.mp3 cassandra.mp4 castrol.mp4 picasa.map picasa.mp4 Определите, по какой из перечисленных масок из этих 7 файлов будет отобрана указанная группа файлов: cascad.mpeg cassa.mp3 cassandra.mp4 picasa.mp4 1) *cas*a*.mp* 2) *ca*a*.mp* 3) *cas*.mp* 4) *cas*a*.mp?

Решение:
Предложенная маска должна подходить к четверым отобранным, а к остальным – нет, иначе они тоже отберутся
1) *cas*a*.mp*
*cascad.mpeg подходит
*cassa*.mp3 подходит
*cassandra.mp4 подходит
picas*a*.mp4 подходит
carga.mp3 (после а нет s) не подходит
castrol.mp4 (после s нет а) не подходит
picasa.map (между m и p символов не должно быть) не подходит
2) *ca*a*.mp*
*carga*.mp3 подходит, а не должен

3) *cas*.mp*
*castrol.mp4 подходит, а не должен
4) *cas*a*.mp?
*cascad.mpeg не подходит, а должен

Ответ: 1

Каждая строка таблицы 2 содержит информацию о ребёнке и

об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведённых данных фамилию и инициалы дяди Леоненко В.С. Пояснение: дядей считается брат отца или матери. 1) Геладзе И.П. 2) Геладзе П.И. 3) Гнейс А.С. 4) Леоненко Н.А.

Решение:

Леоненко В.С. ж, 35

Леоненко А.И. ж, (мама) 34

Леоненко С.С. м, (папа) 33

Геладзе И.П. м, (дед) 23

Гнейс. А.С.
ж, (бабушка) 44

Леоненко И.А. ж, (бабушка) 14

Геладзе П.И.
м, (дядя) 24

Ответ: 2

519?
Решение:

Подсчитываем единицы

Ответ: 4

E, F, G построены дороги, протяжённость которых приведена в

таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

Решение:

А

B

D

C

E

F

G

25

5

8

12

2

4

5

10

5

5

Необходимо добраться от A до G.
Проверим возможные варианты
A – G =25
A – B – D – C – G = 5+8+2+10 = 25
A – D – C – G = 12+2+10 = 24
A – D – C – F – G = 12+2+5+5 = 24
A – D – C – E – G = 12+2+4+5 = 23

Ответ: 23

этому числу строится новое число по следующим правилам. 1. Складываются

первая и вторая, а также третья и четвёртая цифры исходного числа. 2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей). Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114. Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

Решение:
1311
13 = 4 + 9 – минимальное число 49
11 = 2 + 9 – минимальное число 29
2949

Ответ: 2949

номера: 1. прибавь 1,

2. умножь на 2. Первая из них увеличивает число на экране на 1, вторая удваивает его. Например, 2121 – это программа умножь на 2 прибавь 1 умножь на 2 прибавь 1, которая преобразует число 1 в число 7. Запишите порядок команд в программе преобразования числа 3 в число 63, содержащей не более 8 команд, указывая лишь номера команд. Если таких программ более одной, то запишите любую из них.

Решение:
3 – 63, команда 1 +1 и команда 2 *2
63 – 3 проще выполнять задание в обратном порядке, тогда команда 1 -1 и команда 2 /2
63 – 1 = 62 (1) номер команды
62 / 2 = 31 (2)
31 – 1 = 30 (1)
30 / 2 = 15 (2)
15 – 1 = 14 (1)
14 / 2 = 7 (2)
7 – 1 = 6 (1)
6 / 2 = 3 (2)
Запишем команды в обратном порядке: 21212121

Ответ: 21212121

два команды, которым присвоены номера: 1. прибавь 3, 2.

умножить на х. Первая из них увеличивает число на экране на 3, вторая умножает на х. Программа для исполнителя – это последовательность номеров команд. Известно, что программа 12112 преобразует число 3 в число 120. Определите значение х, если известно, что оно натуральное.

Решение:
3+3=6 (1)
6х (2)
6х+3 (1)
6х+3+3 = 6х+6 (1)
(6х+6)х (2)
(6х+6)6 = 120
6х2 + 6х – 120 = 0

Ответ: 4

таблицу квадратов двузначных чисел от 20 до 59. Для этого

сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 2 до 5. Затем в ячейку В5 записал формулу квадрата двузначного числа (А5 – число десятков; В1 – число единиц), после чего скопировал её во все ячейки диапазона B2:К5. В итоге получил таблицу квадратов двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы. В ячейке B5 была записана одна из следующих формул: 1) =(B1+10*A5)^2 2) =($B1+10*$A5)^2 3) =(B$1+10*$A5)^2 4) =($B1+10*A$5)^2 Укажите в ответе номер формулы, которая была записана в ячейке B5 Примечание: знак $ используется для обозначения абсолютной адресации.

Решение:
3) =(B$1+10*$A5)^2 = (0 + 10 * 5) ^ 2 = 50 ^ 2 = 2500
Первая строка должна быть постоянной, иначе будут складываться большие числа из второй, третьей и т.д. строк, следовательно перед цифрой 1 должен стоять знак $.
Первый столбец должен быть постоянным, иначе будут складываться большие числа из второго, третьего и т.д. столбцов, следовательно перед буквой А должен стоять знак $.

Ответ: 3

должно быть записано в ячейке A1, чтобы диаграмма, построенная

по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Ответ: 5

выполнения программы.
Решение:
s = 33
n = 1
пока S > 0
1)

s = s – 7 = 33 – 7 = 26
n = n*3 = 1*3 = 3
2) s = s – 7 = 26 – 7 = 19
n = n*3 = 3*3 = 9
3) s = s – 7 = 19 – 7 = 12
n = n*3 = 9*3 = 27
4) s = s – 7 = 12 – 7 = 5
n = n*3 = 24*3 = 81
5) s = s – 7 = 5 – 7 = -2
n = n*3 = 81*3 = 243

Или можно определить таким образом:
s = s – 7*5 = 33 – 7*5 = -2
n = n*35 = 1*35 = 243

Ответ: 243

64 кГц и 24-битным разрешением. В результате был получен

файл размером 120 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5.

Ответ: 5

одного компьютера на другой двумя способами. А. Сжать архиватором,

передать архив по каналу связи, распаковать. Б. Передать по каналу связи без использования архиватора. Какой способ быстрее и насколько, если:  средняя скорость передачи данных по каналу связи составляет 223 бит в секунду;  объём сжатого архиватором документа равен 90% исходного;  время, требуемое на сжатие документа, – 16 секунд, на распаковку – 2 секунды? В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Единицы измерения «секунд», «сек.», «с» к ответу добавлять не нужно.

Ответ: Б14

доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость

получения информации 220 бит в секунду. У Сергея нет скоростного доступа в Интернет, но есть возможность получать информацию от Тани по телефонному каналу со средней скоростью 214 бит в секунду. Сергей договорился с Таней, что та будет скачивать для него данные объёмом 10 Мбайт по высокоско­ростному каналу и ретранслировать их Сергею по низкоскоростному каналу. Компьютер Тани может начать ретрансляцию данных не раньше чем им будут получены первые 2 Мбайт этих данных. Каков минимально возможный промежуток времени (в се­кундах) с момента начала скачивания Таней данных до полного их получения Сергеем? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Ответ: 5136

Л, Р, Т, записаны в алфавитном порядке и пронумерованы.

Вот начало списка: 1. КККК 2. КККЛ 3. КККР 4. КККТ …… Запишите слово, которое стоит под номером 67.

Решение:
44 = 256 строк (основание – К, Л, Р, Т; степень – четыре символа)
1 столбец 256 / 4 = 64 (по 64 «К», по 64 «Л», по 64 «Р», по 64 «Т»)
2 столбец 64 / 4 = 16
3 столбец 16 / 4 = 4
4 столбец 4 / 4 = 1

67 строка

1
1 К
по 64 .
.
64 К
65 Л
по 64 .
.
128 Л
129 Р
по 64 .
.
192 Р
193 Т
по 64 .
.
256 Т

Л

2
65 К
по 16 .
.
80 К
81 Л
по 16 .
.
96 Л
97 Р
по 16 .
.
112 Р
113 Т
по 16 .
.
128 Т

К

3
65 К
66 К
67 К
68 К
69 Л
70 Л
71 Л
72 Л
73 Р
74 Р
75 Р
76 Р
77 Т
78 Т
79 Т
80 Т

К

4
65 К
66 Л
67 Р
68 Т

Р

Ответ: ЛККР

Л, Р, Т, записаны в алфавитном порядке и пронумерованы.

Вот начало списка: 1. КККК 2. КККЛ 3. КККР 4. КККТ …… Запишите слово, которое стоит под номером 67.

Решение (другой способ):
Заменим К, Л, Р, Т на 0, 1, 2, 3 соответственно.
По­лу­чен­ная за­пись есть числа, за­пи­сан­ные в чет­ве­рич­ной си­сте­ме счис­ле­ния в по­ряд­ке воз­рас­та­ния. Тогда на 67-м месте будет сто­ять число 66 (т. к. пер­вое число 0). Пе­ре­ведём число 66 в чет­ве­рич­ную си­сте­му

Ответ: ЛККР

В чет­ве­рич­ной си­сте­ме 66 за­пи­шет­ся как 1002 (четыре цифры соответствует
4-буквенному слову). Про­из­ведём об­рат­ную за­ме­ну и по­лу­чим ЛККР.

символьных последователей длины 6 в трехбуквенном алфавите {A, B,

C}, которые содержат ровно три буквы А.

Ответ: 160

символьных последователей длины 6 в четырехбуквенном алфавите {A, B,

C, D}, которые содержат не менее двух букв А.

символьных последователей длины 6 в четырехбуквенном алфавите {A, B,

C, D}, которые содержат не менее двух букв А.

символьных последователей длины 6 в четырехбуквенном алфавите {A, B,

C, D}, которые содержат не менее двух букв А.

символьных последователей длины 6 в четырехбуквенном алфавите {A, B,

C, D}, которые содержат не менее двух букв А.

символьных последователей длины 6 в четырехбуквенном алфавите {A, B,

C, D}, которые содержат не менее двух букв А.

Решение:
И, наконец, все буквы А. Такой вариант 1, формулы использовать не нужно.
Просуммируем все полученные результаты:
1215 + 540 + 135 + 18 + 1 = 1909

Ответ: 1909

составленные из букв А, О, У записаны в алфавитном

порядке и пронумерованы. Вот начало списка: 1. ААААА 2. ААААО 3. ААААУ 4. АААОА …… Под каким номером стоит слово ООАУУ?.

Решение:
За­ме­ним буквы А, О, У на 0, 1, 2 со­от­вет­ствен­но (для них по­ря­док оче­ви­ден – по воз­рас­та­нию).
По­лу­чен­ная за­пись есть числа, за­пи­сан­ные в троич­ной си­сте­ме счис­ле­ния в по­ряд­ке воз­рас­та­ния. За­пи­шем слово ООАУУ в т­роич­ной си­сте­ме: 11022 и пере­ведём его в де­ся­тич­ную:
4 3 2 1 0
110223 = 1*34 +1*33 + 0*32 + 2*31 + 2*30 = 81 + 27 + 6 + 2 = 11610

Не за­бу­дем о том, что есть слово номер 1, за­пи­сы­ва­ю­ще­е­ся как 0, а зна­чит, 116 — число, со­от­вет­ству­ю­щее но­ме­ру 117.

Ответ: 117

составленные из букв A, B, C, D, записаны в

алфавитном порядке и пронумерованы. Вот начало списка: 1. AAAAA 2. AAAAB 3. AAAAC 4. AAAAD 5. AAABA 6. AAABB …… Запишите слово, которое стоит под номером 81 от начала списка.

Решение:
Заменим A, B, C, D на 0, 1, 2, 3 соответственно.
По­лу­чен­ная за­пись есть числа, за­пи­сан­ные в чет­ве­рич­ной си­сте­ме счис­ле­ния в по­ряд­ке воз­рас­та­ния. Тогда на 81-м месте будет сто­ять число 80 (т. к. пер­вое число 0). Пе­ре­ведём число 80 в чет­ве­рич­ную си­сте­му

Ответ: ABBAA

В чет­ве­рич­ной си­сте­ме 80 за­пи­шет­ся как 01100 (в начале 0, т.к. слово должно быть 5-буквенным). Про­из­ведём об­рат­ную за­ме­ну и по­лу­чим ABBAA.

F. Чему равна сумма всех чисел, напечатанных на экране

при выполнении вызова F(1)?

Решение: Сразу печатается n на экран. Далее проверяется условие (n<5), и вызывается функция два раза, но уже в измененном виде.

1

1

Вызывается 1 и печатается тоже 1.

n < 5, т.е. 1 < 5, да, вызывается функция F(n+1) и F(n+3)

2

4

Печатается 2 и 4

2

4

Дальше проверяются все значения, если условие выполняется, то вызывается функция F(n+1) и F(n+3)

3

5

3

5

5

7

5

7

4

5

4

5

5

7

5

7

Суммируем все напечатанные числа
S = 1+2+4+3+5+5+7+4+5+5+7=49

Ответ: 49

32-разрядная двоичная (то есть состоящая из нулей и единиц)

последовательность. Маска определяет, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети. IP-адрес узла: 217.8.244.3 Маска: 255.255.252.0 При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в нужном порядке соответствующие им буквы без использования точек. Пример. Пусть искомый IP-адрес: 192.168.128.0, и дана таблица В этом случае правильный ответ будет записан в виде: HBAF

Решение:
25510 = 111111112, следовательно, при умножении на любое другое число, получится это число
При умножении на 0 получим 0
В итоге получаем 217.8.ХХХ.0
Необходимо найти 24410 и 25210 в двоичном виде, их конъюнктивно умножить, и перевести в десятичный вид

TCP/IP маской сети называется двоичное число, определяющее, какая часть

IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, - в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Для узла с IP-адресом 136.206.24.114 адрес сети равен 136.204.0.0. Чему равен второй слева байт маски? Ответ запишите в виде десятичного числа.

Решение:
IP-адрес узла: 136.206.24.114
Маска: ххх.yyy.ххх.ххх
IP-адрес сети: 136.204.0.0
В нашем случаи надо найти ууу
Остальные тоже можно найти: 255.ууу.0.0.
25510 = 111111112, следовательно, при умножении на любое другое число, получится это число.
Необходимо найти 20610 и 20410 в двоичном виде

TCP/IP маской сети называется двоичное число, определяющее, какая часть

IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, - в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Для узла с IP-адресом 136.206.24.114 адрес сети равен 136.204.0.0. Чему равен второй слева байт маски? Ответ запишите в виде десятичного числа.

Решение:
Необходимо найти 20610 и 20410 в двоичном виде

Здесь однозначные ответы. В задании указано, что в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули, следовательно

TCP/IP маской сети называется двоичное число, определяющее, какая часть

IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, - в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Для узла с IP-адресом 136.206.24.114 адрес сети равен 136.204.0.0. Чему равен второй слева байт маски? Ответ запишите в виде десятичного числа.

Решение:

Переведем 111111002 в десятичный вид:
7 6 54 32 1 0
111111002 = 27 + 26 + 25 + 24 + 23 + 22 = 128+64+32+16+8+4=25210

Ответ: 252

TCP/IP маской сети называется двоичное число, определяющее, какая часть

IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, - в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите второй слева байт адреса сети. IP-адрес узла: 14.8.192.131 Маска: 255.255.192.0 Ответ запишите в виде десятичного числа.

Решение:
IP-адрес узла: 14.8.192.131
Маска: 255.255.192.0
IP-адрес сети: ххх.yyy.ххх.ххх
В нашем случаи надо найти ууу.
25510 = 111111112, следовательно, при умножении на любое другое число, получится это число, т.е. 8.
Другие числа тоже при желании можно найти:
14.8.192.0

Ответ: 8

выдаётся пароль, состоящий из 15 символов и содержащий только

символы Ш, К, О, Л, А (таким образом, используется 5 различных символов). Каждый такой пароль в компьютерной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Укажите объём памяти в байтах, отводимый этой системой для записи 30 паролей. В ответе запишите только число, слово «байт» писать не нужно.

Решение:
Ш, К, О, Л, А – 5 символов, чтобы их закодировать нужны 3 бита, т.е. 23 = 8 (8 >= 5)
Чтобы закодировать один пароль с 15 символами:
3 * 15 = 45 бит
При этом необходимо целое количество байт (6 байт):

Для записи 30 паролей требуется:
6 * 30 = 180 байт

Ответ: 180

след в виде линии. Чертёжник может выполнять команду сместиться

на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1). Цикл ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, при этом n > 1): НАЧАЛО сместиться на (–3, –3) ПОВТОРИ n РАЗ сместиться на (a, b) сместиться на (27, 12) КОНЕЦ ПОВТОРИ сместиться на (–22, -7) КОНЕЦ Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.

РАЗ сместиться на (a, b) сместиться на (27, 12) КОНЕЦ ПОВТОРИ сместиться на

(–22, -7) КОНЕЦ Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.

Решение:
Чертежник после выполнения данного алгоритма, возвращается в исходную точку. Следовательно сумма значений по осям абсцисс и ординат должны равняться нулю.
-3 и -22 дают -25. Внутри цикла 27 (27-25=2), следовательно, a должен быть меньше 0.
Аналогично, -3 и -7 дают -10. Внутри цикла 12 (12-10=2), b также меньше 0.
Учитывая, что а и b меньше 0, запишем следующие уравнения:
X: -3 – a*n + 27*n – 22 = 0
Y: -3 – b*n + 12*n – 7 = 0, при n > 1, a < 0, b < 0.

РАЗ сместиться на (a, b) сместиться на (27, 12) КОНЕЦ ПОВТОРИ сместиться на

(–22, -7) КОНЕЦ Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.

Решение:
X: -3 – a*n + 27*n – 22 = 0
Y: -3 – b*n + 12*n – 7 = 0, при n > 1, a < 0, b < 0.
Рассмотрим первое уравнение, переписав его
27*n – a*n = 22+3
n*(27-a) = 25, т.к. 25 можно представить как 5*5, то
n*(27-a) = 5*5 и будет, что n = 5, и 27 – а = 5, т.е. а = 22
Аналогично, если рассмотри второе уравнение:
n*(12-b) = 10, т.к. n = 5, то b = 10
Не должен смущать тот момент, что a = 22, b = 10, т.е. положительные. Мы учитывали это и в уравнении указали.

Ответ: 5

А, Б, В, Г, Д, Е, Ж, И, К,

Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?

Решение:
NЛ = NИ + NД + NЖ + NК
NK = NЕ
NИ = NД
NЖ = NЕ + NВ
NЕ = NГ
NД = NБ + NВ
NГ = NА
NВ = NБ + NА + NГ
NБ = NА
NА

= 1

= 1

= 1 + 1 + 1 = 3

= 1

= 1 + 3 = 4

= 1

= 1 + 3 = 4

= 4

= 1

= 4 + 4 + 4 + 1 = 13

Ответ: 13

схема дорог, связывающих города А, Б, В, Г, Д,

Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М и проходящих через город Г?

Решение:
Дорогу Б – В не рассматриваем, т.к. до города В не возможно добраться через город Г (а это условие задачи).
Также не рассматриваем дорогу Д – Ж.
NМ = NИ + NЕ + NК
NK = NЕ + NЖ
NИ = NВ + NЕ
NЖ = NГ
NЕ = NВ + NГ + NЖ
NД = NА
NГ = NА + NБ + NД
NВ = 0
NБ = NА
NА

= 1

Ответ: 21

= 1

= 1

= 1 + 1 + 1 = 3

= 3

= 0 + 3 + 3 = 6

= 0 + 6 = 6

= 6 + 3 = 9

= 6 + 6 + 9 = 21

схема дорог, связывающих города А, Б, В, Г, Д,

Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М и не проходящих через город Г?

Решение:
Дороги, проходящие через город Г не рассматриваем.
NМ = NИ + NЕ + NК
NK = NЕ + NЖ
NИ = NВ + NЕ
NЖ = NД
NЕ = NВ + NЖ
NД = NА
NВ = NБ
NБ = NА
NА

= 1

Ответ: 8

= 1

= 1

= 1

= 1

= 1 + 1 = 2

= 1 + 2 = 3

= 2 + 1 = 3

= 3 + 2 + 3 = 8

выражения: 42014 + 22015 – 8?
Решение:
Преобразуем: (22014)2 + 22015

– 23 = 24028 + 22015 – 23
24028 = 10…..02 22015 = 10..…02

4028 нулей 2015 нулей
Если их прибавить, получим:

4028 чисел
10………........010…….........0

2012 нулей 2015 нулей (4028 – 2015 – 1 = 2012)
Отнимем от этого числа 23 = 10002
10………….001…………..1000

2012 нулей 2012 единиц и 3 нуля
1 + 2012 = 2013 единиц

Ответ: 2013

натурального числа х справедливо равенство: 3222х+1 – 3122х+2 +

8910 = 0 Определите значение х. Ответ запишите в десятичной системе счисления.

Решение:
2 1 0 2 1 0
3222х+1 – 3122х+2 + 8910 = 0
3(2х+1)2 + 2(2х+1) + 2 – (3(2х+1)2 + 2х + 2 + 2) + 89 = 0
3(4х2+4х+1) + 4х+2 + 2 – (3(4х2 +8х+4) + 2х + 4) + 89 = 0
12х2 + 12х+ 3 + 4х+ 4 – (12х2 +24х+12 + 2х + 4) + 89 = 0
12х2 + 16х+ 7– 12х2 – 26х – 16 + 89 = 0
-10х = -80
х = 8
Можно проверить,
32217 – 31218 + 8910 = 0
903 – 992 + 89 = 0

Ответ: 8

в системе счисления с основание N оканчивается на 0,

и в его записи присутствуют только цифры от 0 до 9. Чему равно основание этой системы счисления N?

Решение:
Чтобы число оканчивалось на 0, число 247 в начале должно делиться без остатка. В остальных случаях остаток не должен превосходить цифру 9, значит система счисления будет больше 10.
247 без остатка делится на 13.
Проверим






16013
Подходит, все цифры в диапазоне от 0 до 9 и заканчивается на 0

Ответ: 13

в системе счисления с основание N оканчивается на 2

и содержит 5 цифр. Чему равно основание этой системы счисления N?

Решение:
Чтобы число оканчивалось на 2, от 107 необходимо отнять 105.
105 можно получить через 5*21 и 3*35
Проверим их






4125
Не подходит, т.к. 3 цифры
112223
Подходит, 5 цифр и заканчивается на 2

Ответ: 3

логической операции «ИЛИ» используется символ «|», а для обозначения

логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в сотнях тысяч) будет найдено по запросу Подкова & Наковальня? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:
С таблицы видно, что Ухо & Подкова страниц не имеет, значит круги Эйлера будут иметь вид:

= [37; 60] и Q = [40; 77]. Укажите

наименьшую возможную длину такого отрезка A, что формула истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х.

Решение:
Варианты для A [37;40], [40;60], [60;77]. Проверяем каждый:
A = [37;40]
(-∞;37] 0 → ((0 ^ 1) → 1) = 0 → (0 → 1) = 0 → 1 = 1
[37;40] 1 → ((0 ^ 0) → 0) = 1 → (0 → 0) = 1 → 1 = 1
[40;60] 1 → ((1 ^ 1) → 0) = 1 → (1 → 0) = 1 → 0 = 0
Не подходит при A = [37;40]
A = [40;60]
(-∞;37] 0 → ((0 ^ 1) → 1) = 0 → (0 → 1) = 0 → 1 = 1
[37;40] 1 → ((0 ^ 1) → 0) = 1 → (0 → 0) = 1 → 1 = 1
[40;60] 1 → ((1 ^ 0) → 0) = 1 → (0 → 0) = 1 → 1 = 1
[60;77] 0 → ((1 ^ 1) → 1) = 0 → (1 → 1) = 0 → 1 = 1
(77;∞] 0 → ((0 ^ 1) → 1) = 0 → (0 → 1) = 0 → 1 = 1
Подходит при A = [40;60]. Длина = 20
A = [60;77]
(-∞;37] 0 → ((0 ^ 1) → 1) = 0 → (0 → 0) = 0 → 0 = 1
[37;40] 1 → ((0 ^ 1) → 0) = 1 → (0 → 0) = 1 → 1 = 1
[40;60] 1 → ((1 ^ 1) → 0) = 1 → (1 → 0) = 1 → 0 = 0
Не подходит при A = [60;77]

+

+

-

+

+

+

+

+

+

+

-

Ответ: 20

с индексами от 0 до 9. Значения элементов равны

6; 9; 7; 2; 1; 5; 0; 3; 4; 8 соответственно, т.е. A[0] = 6; A[1] = 9 и т.д. Определите значение переменной c после выполнения следующего фрагмента программы

Решение:

i: = 1; A[i-1] < A[i]
A[0] < A[1]; 6 < 9, да
c:= c +1 = 0 + 1 = 1
t:= A[i]; t:= A[1] = 9
A[i]:= A[i-1]; A[1]:= A[0] = 6
A[i-1]:= t; A[0]:= 9
c = 1; A[0] = 9; A[1] = 6

i: = 2; A[i-1] < A[i]
A[1] < A[2]; 6 < 7, да
c:= c +1 = 1 + 1 = 2
t:= A[i]; t:= A[2] = 7
A[i]:= A[i-1]; A[2]:= A[1] = 6
A[i-1]:= t; A[1]:= 7
c = 2; A[1] = 7; A[2] = 6

i: = 3; A[i-1] < A[i]
A[2] < A[3]; 6 < 2, нет
c = 2; A[2] = 6; A[3] = 2

i: = 4; A[i-1] < A[i]
A[3] < A[4]; 2 < 1, нет
c = 2; A[3] = 2; A[4] = 1

фрагмента программы
Решение:


i: = 5; A[i-1] < A[i]

A[4] < A[5]; 1 < 5, да
c:= c +1 = 2 + 1 = 3
t:= A[i]; t:= A[5] = 5
A[i]:= A[i-1]; A[5]:= A[4] = 1
A[i-1]:= t; A[4]:= 5
c = 3; A[4] = 5; A[5] = 1

i: = 7; A[i-1] < A[i]
A[6] < A[7]; 0 < 3, да
c:= c +1 = 3 + 1 = 4
t:= A[i]; t:= A[7] = 3
A[i]:= A[i-1]; A[7]:= A[6] = 0
A[i-1]:= t; A[6]:= 3
c = 4; A[6] = 3; A[7] = 0

i: = 6; A[i-1] < A[i]
A[5] < A[6]; 1 < 0, нет
c = 3; A[5] = 1; A[6] = 0

i: = 8; A[i-1] < A[i]
A[7] < A[8]; 0 < 4, да
c:= c +1 = 4 + 1 = 5
t:= A[i]; t:= A[8] = 4
A[i]:= A[i-1]; A[8]:= A[7] = 0
A[i-1]:= t; A[7]:= 4
c = 5; A[7] = 4; A[8] = 0

i: = 9; A[i-1] < A[i]
A[8] < A[9]; 0 < 8, да
c:= c +1 = 5 + 1 = 6
t:= A[i]; t:= A[9] = 8
A[i]:= A[i-1]; A[8]:= A[8] = 0
A[i-1]:= t; A[8]:= 8
c = 6; A[8] = 8; A[9] = 0

Ответ: 6

целочисленный массив с индексами от 0 до 10. Ниже

представлен записанный на разных языках программирования фрагмент одной и той же программы, обрабатывающей данный массив.

Решение:
В пе­ре­мен­ную s за­пи­сы­ва­ет­ся сле­ду­ю­щая сумма:
s = 0 + (2*A[0] – A[1]) + (2*A[1] – A[2]) + (2*A[2] – A[3]) + (2*A[3] – A[4]) + (2*A[4] – A[5]) +
+ (2*A[5] – A[6]) + (2*A[6] – A[7]) + (2*A[7] – A[8]) + (2*A[8] – A[9]) + (2*A[9] – A[10]) =
= 2*A[0] + A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] + A[9] – A[10]
В массиве находились двухзначные натуральные числа.
Чтобы эта сумма была наименьшей, A[0]… A[9] должны быть наименьшими, а A[10] – наибольшим.
Это получается в следующем случае:
2*10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 – 99 = 110 – 99 = 11

В начале выполнения этого фрагмента в массиве находились двухзначные натуральные числа. Какое наименьшее значение может иметь переменная s после выполнения данной программы?

Ответ: 11

целочисленный массив с индексами от 0 до 10. Ниже

представлен записанный на разных языках программирования фрагмент одной и той же программы, обрабатывающей данный массив.

Решение:
В пе­ре­мен­ную s за­пи­сы­ва­ет­ся сле­ду­ю­щая сумма:
s = 0 + (2*A[0] + A[1]) + (2*A[1] + A[2]) + (2*A[2] + A[3]) + (2*A[3] + A[4]) + (2*A[4] + A[5]) +
+ (2*A[5] + A[6]) + (2*A[6] + A[7]) + (2*A[7] + A[8]) + (2*A[8] + A[9]) + (2*A[9] + A[10]) =
= 2*A[0] + 3*A[1] + 3*A[2] + 3*A[3] + 3*A[4] + 3*A[5] + 3*A[6] + 3*A[7] + 3*A[8] + 3*A[9] + A[10]
В массиве находились двухзначные нечетные натуральные числа.
Чтобы эта сумма была наибольшей, A[0]… A[10] должны быть наибольшими, причем нечетными.
Это получается в следующем случае:
2*99 + 3*99*9 + 99 = 198 + 2673 + 99 = 2970

В начале выполнения этого фрагмента в массиве находились двухзначные нечётные натуральные числа. Какое наибольшее значение может иметь переменная s после выполнения данной программы?

Ответ: 2970

целочисленный массив с индексами от 0 до 10. Ниже

представлен записанный на разных языках программирования фрагмент одной и той же программы, обрабатывающей данный массив.

Решение:
В пе­ре­мен­ную s за­пи­сы­ва­ет­ся сле­ду­ю­щее произведение:
s = 1 * (A[1] * A[10]) * (A[2] * A[9]) * (A[3] * A[8])
В массиве находились однозначные натуральные числа, кратные 3, т.е. 3, 6 и 9.
Чтобы это произведение было наименьшей, A[1]… A[10] должны быть наименьшими, т.е. 3.
Это получается в следующем случае:
1 * 3 * 3 * 3 * 3 * 3 * 3 = 3 ^ 6 = 729

В начале выполнения этого фрагмента в массиве находились однозначные натуральные числа, кратные 3. Какое наименьшее значение может иметь переменная s после выполнения данной программы?

Ответ: 729

на вход число x, этот алгоритм печатает два числа:

a и b. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 15.

Решение:
Из алгоритма видно, что b = b * (x mod 10), т.е. число 15 получается путем умножения двух чисел. Минимальное число, подходящее - это 35 (3*5=15)

Проверим:
a = 0; b = 1; x =35
1) x > 0; 35 > 0, да
а = а + 1 = 0 + 1 = 1
b = b * (x mod 10) = 1 * 35 mod 10 = 1 * 5 = 5
x = x div 10 = 35 div 10 = 3
a = 1; b = 5; x = 3

2) x > 0; 3 > 0, да
а = а + 1 = 1 + 1 = 2
b = b * (x mod 10) = 5 * 3 mod 10 = 5 * 3 = 15
x = x div 10 = 3 div 10 = 0
a = 2; b = 15; x = 0

3) x > 0; 0 > 0, нет

Ответ: 35

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 8.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 2.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть двузначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 8, а М := x mod 10, т.е. М должен иметь цифру 8.
Проверим максимальное двухзначное число, имеющее цифру 8 – 98.
1) x > 0, 98 > 0, да, L := L+1 = 0+1 =1,
if M < (x mod 10), 0 < 98 mod 10, 0 < 8, да
M := x mod 10 = 98 mod 10 = 8,
x := x div 10 = 98 div 10 = 9
2) x > 0, 9 > 0, да, L := L+1 = 1+1 =2,
if M < (x mod 10), 8 < 9 mod 10, 8 < 9, да
M := x mod 10 = 9 mod 10 = 9,
x := x div 10 = 9 div 10 = 0

3) x > 0; 0 > 0, нет
Выходим из цикла и печатаем 2 и 9. Не подходит, должны печатать 2 и 8. Соответственно и первая цифра должна быть 8. Проверим:

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 8.

Решение:

88
1) x > 0, 88 > 0, да, L := L+1 = 0+1 =1,
if M < (x mod 10), 0 < 88 mod 10, 0 < 8, да
M := x mod 10 = 88 mod 10 = 8,
x := x div 10 = 88 div 10 = 8
2) x > 0, 8 > 0, да, L := L+1 = 1+1 =2,
if M < (x mod 10), 8 < 8 mod 10, 8 < 8, нет
M := 8,
x := x div 10 = 8 div 10 = 0

3) x > 0; 0 > 0, нет
Выходим из цикла и печатаем 2 и 8.

Ответ: 88

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 8.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 8, а М := x mod 10, т.е. М должен иметь цифру 8.
Проверим минимальное трехзначное число, имеющее цифру 8 – 108.
1) x > 0, 108 > 0, да, L := L+1 = 0+1 = 1,
if M < (x mod 10), 0 < 108 mod 10, 0 < 8, да
M := x mod 10 = 108 mod 10 = 8,
x := x div 10 = 108 div 10 = 10
2) x > 0, 10 > 0, да, L := L+1 = 1+1 = 2,
if M < (x mod 10), 8 < 10 mod 10, 8 < 0, нет
M := 8,
x := x div 10 = 10 div 10 = 1

3) x > 0; 1 > 0, да L := L+1 = 2+1 = 3,
if M < (x mod 10), 8 < 1 mod 10, 8 < 1, нет
M := 8,
x := x div 10 = 1 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 8.

Ответ: 108

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 9.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 9, а М := x mod 10, т.е. М должен иметь цифру 9.
Проверим минимальное трехзначное число, имеющее цифру 9 – 109.
1) x > 0, 109 > 0, да, L := L+1 = 0+1 = 1,
if M < (x mod 10), 0 < 109 mod 10, 0 < 9, да
M := x mod 10 = 109 mod 10 = 9,
x := x div 10 = 109 div 10 = 10
2) x > 0, 10 > 0, да, L := L+1 = 1+1 = 2,
if M < (x mod 10), 9 < 10 mod 10, 9 < 0, нет
M := 9,
x := x div 10 = 10 div 10 = 1

3) x > 0; 1 > 0, да L := L+1 = 2+1 = 3,
if M < (x mod 10), 9 < 1 mod 10, 9 < 1, нет
M := 9,
x := x div 10 = 1 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 9.

Ответ: 109

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 9.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 9, а М := x mod 10, т.е. М должен иметь цифру 9.
Проверим максимальное трехзначное число, имеющее цифру 9 – 999.
1) x > 0, 999 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 999 mod 10, 9 > 9, нет
M := 9,
x := x div 10 = 999 div 10 = 99
2) x > 0, 99 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 9 > 99 mod 10, 9 > 9, нет
M := 9,
x := x div 10 = 99 div 10 = 9

3) x > 0; 9 > 0, да L := L+1 = 2+1 = 3,
if M > (x mod 10), 9 > 9 mod 10, 9 > 9, нет
M := 9,
x := x div 10 = 9 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 9.

Ответ: 999

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 5.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 2.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть двухзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 5, а М := x mod 10, т.е. М должен иметь цифру 5.
Проверим максимальное двухзначное число, имеющее цифру 5 – 95.
1) x > 0, 95 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 95 mod 10, 9 > 5, да
M := x mod 10 = 95 mod 10 = 5,
x := x div 10 = 95 div 10 = 9
2) x > 0, 9 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 5 > 9 mod 10, 5 > 9, нет
M := 5,
x := x div 10 = 9 div 10 = 0

3) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 2 и 5.

Ответ: 95

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 8.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 2.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть двухзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 8, а М := x mod 10, т.е. М должен иметь цифру 8.
Проверим максимальное двухзначное число, имеющее цифру 8 – 98.
1) x > 0, 98 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 98 mod 10, 9 > 8, да
M := x mod 10 = 98 mod 10 = 8,
x := x div 10 = 98 div 10 = 9
2) x > 0, 9 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 8 > 9 mod 10, 8 > 9, нет
M := 8,
x := x div 10 = 9 div 10 = 0

3) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 2 и 8.

Ответ: 98

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 0.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 0, а М := x mod 10, т.е. М должен иметь цифру 0.
Проверим максимальное трехзначное число, имеющее цифру 0 – 990.
1) x > 0, 990 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 990 mod 10, 9 > 0, да
M := x mod 10 = 990 mod 10 = 0,
x := x div 10 = 990 div 10 = 99
2) x > 0, 99 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 0 > 99 mod 10, 0 > 9, нет
M := 0,
x := x div 10 = 99 div 10 = 9

3) x > 0; 9 > 0, да L := L+1 = 2+1 = 3,
if M > (x mod 10), 0 > 9 mod 10, 0 > 9, нет
M := 0,
x := x div 10 = 9 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 0.

Ответ: 990

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 0.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 0, а М := x mod 10, т.е. М должен иметь цифру 0.
Проверим минимальное трехзначное число, имеющее цифру 0 – 100.
1) x > 0, 100 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 100 mod 10, 9 > 0, да
M := x mod 10 = 100 mod 10 = 0,
x := x div 10 = 100 div 10 = 10
2) x > 0, 10 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 0 > 10 mod 10, 0 > 0, нет
M := 0,
x := x div 10 = 10 div 10 = 1

3) x > 0; 1 > 0, да L := L+1 = 2+1 = 3,
if M > (x mod 10), 0 > 1 mod 10, 0 > 1, нет
M := 0,
x := x div 10 = 1 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 0.

Ответ: 100

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Сколько существуют таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 5.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 5, а М := x mod 10, т.е. М должен иметь цифру 5. Среди цифр не должны встречаться цифры 0, 1, 2, 3 и 4, иначе программа их и выведет. Проверим любое такое трехзначное число.
1) x > 0, 125 > 0, да, L := L+1 = 0+1 = 1,
if M > (x mod 10), 9 > 125 mod 10, 9 > 5, да
M := x mod 10 = 125 mod 10 = 5,
x := x div 10 = 125 div 10 = 12
2) x > 0, 12 > 0, да, L := L+1 = 1+1 = 2,
if M > (x mod 10), 9 > 12 mod 10, 9 > 2, да
M := x mod 10 = 12 mod 10 = 2,
x := x div 10 = 12 div 10 = 1

3) x > 0; 1 > 0, да L := L+1 = 2+1 = 3,
if M > (x mod 10), 9 > 1 mod 10, 9 > 1, да
M := x mod 10 = 1 mod 10 = 1,
x := x div 10 = 1 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 1. Второе число не подходит, печатается самая маленькая цифра. В итоге самая маленькая цифра должна быть 5

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Сколько существуют таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 5.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 5, а М := x mod 10, т.е. М должен иметь цифру 5. Среди цифр не должны встречаться цифры 0, 1, 2, 3 и 4, иначе программа их и выведет. Подсчитаем эти числа.

555
556
557
558
559

Ответ: 61

565
566
567
568
569

575
576
577
578
579

585
586
587
588
589

595
596
597
598
599

655
656
657
658
659

755
756
757
758
759

855
856
857
858
859

955
956
957
958
959

9*5=45

665
675
685
695

765
775
785
795

865
875
885
895

965
975
985
995

4*4=16

45+16=61

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Сколько существуют таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 2.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 2, а М := x mod 10, т.е. М должен иметь цифру 2. Среди цифр не должны встречаться цифры отличные от 0,1 и 2, иначе программа их и выведет. Проверим любое такое число.
1) x > 0, 125 > 0, да, L := L+1 = 0+1 = 1,
if M < (x mod 10), 0 < 125 mod 10, 0 < 5, да
M := x mod 10 = 125 mod 10 = 5,
x := x div 10 = 125 div 10 = 12
2) x > 0, 12 > 0, да, L := L+1 = 1+1 = 2,
if M < (x mod 10), 5 < 12 mod 10, 5 < 2, нет
M := 5,
x := x div 10 = 12 div 10 = 1

3) x > 0; 1 > 0, да L := L+1 = 2+1 = 3,
if M < (x mod 10), 5 < 1 mod 10, 5 < 1, нет
M := 5,
x := x div 10 = 1 div 10 = 0
4) x > 0, 0 > 0, нет
Выходим из цикла и печатаем 3 и 5. Второе число не подходит, печатается самая большая цифра. В итоге самая большая цифра должна быть 2

программирования записан алгоритм. Получив на вход число x, этот

алгоритм печатает два числа: L и M. Сколько существуют таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 2.

Решение:
Первоначальное значение L:=0, в итоге должно печататься 3.
Из алгоритма видно, что L:=L+1, т.е., чтобы while x>0 выполнялось, х должен быть трехзначным, т.к. x := x div 10, с каждым циклом уменьшается на цифру.

М, должно печататься 2, а М := x mod 10, т.е. М должен иметь цифру 2. Среди цифр не должны встречаться цифры отличные от 0, 1 и 2, иначе программа их и выведет. Подсчитаем все возможные трехзначные числа, содержащие цифры 0, 1, 2.

100
101
102
110
111
112

120
121
122
200
201
202

210
211
212
220
221
222

Уберем из этих чисел те, в которых не встречается цифра 2 и подсчитаем их

Ответ: 14

переменной k, при которых программа выдаёт тот же ответ,

что и при входном значении k = 64. Значение k = 64 также включается в подсчёт различных значений k.

Решение: В программе имеется подпрограмма. В данном случае это функция. Имеет целочисленный параметр (longint) и возвращает в качестве ответа n*n, т.е. квадрат. Пример: f(4)=16.

Первоначально k=64. Определим, что при этом распечатает программа (i).
Имеется цикл с предусловием, while (i>0) and (f(i)>=k).
i=12, f(12) = 144 >= 64, т.е. условие выполняется и i станет 11. Далее:
i=11, f(11) = 121 >= 64
i=10, f(10) = 100 >= 64
i=9, f(9) = 81 >= 64
i=8, f(8) = 64 >= 64
i=7, f(7) = 49 < 64, условие не выполняется и выходим из цикла.
В итоге, когда k=64, на экране печатается 7.
Надо определить такое количество k, при которых будет печататься число 7.
Рассмотрим направление, когда k>64. К примеру 65. Тогда при i=8, f(8) = 64 >= k (т.е. 65) наше условие выполнятся не будет, и программа напечатает 8. А это число не подходит.
Минимальное число должно быть 50, чтобы выполнялось условие i=7, f(7) = 49 < k (т.е. 50).
В итоге диапазон для k=[50…64]. Подсчитаем количество этих чисел
15

Ответ: 15

значение Н нужно ввести, чтобы число, напечатанное в результате

выполнения следующего алгоритма, было наименьшим. Если таких значении несколько, то в ответ запишите максимальное из них.

Ответ: -10

значение Н нужно ввести, чтобы число, напечатанное в результате

выполнения следующего алгоритма, было наибольшим. Если таких значении несколько, то в ответ запишите минимальное из них.

Ответ: 70

У исполнителя три команды, которым присвоены номера:

1. Прибавь 1 2. Прибавь 2 3. Прибавь 4 Первая из них увеличивает число на экране на 1, вторая увеличивает это число на 2, а третья – на 4. Программа для исполнителя Май4 – это последовательность команд. Сколько есть программ, которые число 21 преобразуют в число 30?

Решение:
21 → 30; +1; +2; +4
21 можно получить только одним способом;
22 – от 21 (+1);
23 – от 21 и 22 (22+1 и 21+2)
24 – от 22 и 23 (23+1 и 22+2)
25 – от 21, 23 и 24 и т.д.

Ответ: 96

x1, x2, … x8, y1, y2, … y8, которые

удовлетворяют всем перечисленным ниже условиям? (x1 \/ x2) /\ ((x1 /\ x2) → x3) /\ (¬x1 \/ y1) = 1 (x2 \/ x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1 В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x8, y1, y2, … y8, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Решение:

Начать рассматривать уравнение с последнего (¬x8 \/ y8) = 1, т.к. фигурируют только две переменные

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:
(¬x8 \/ y8) = 1






Нас интересуют три набора: x8=0; y8=0
x8=0; y8=1
x8=1; y8=1

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:
Первый этап, т.е. когда x8=0; y8=0
у встречается только в крайних скобках. Поэтому в начале будем работать с х, а потом отдельно с у.

0

По строке (x7 \/ x8) /\ (¬x7 \/ y7) = 1 видно, что если х8=0, то х7 должен равняться 1, иначе уравнение окажется ложным.
Следовательно, х7=1.

1

По строке (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 видно, что если х7=1, х8=0, то х6 должен равняться 0, иначе уравнение окажется ложным.
Следовательно, х6=0.

0

Далее, аналогично

1

0

1

0

1

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:

Рассмотрим y.
При х8=0, у8=0
Посмотрим на (x7 \/ x8) /\ (¬x7 \/ y7) = 1. Если х7=1, то у7 обязан быть 1, иначе вторая скобка будет 0.
Посмотрим на (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1. При х6=0, у6 может принимать два значения, 0 и 1.
Далее, аналогично, при х5=1, у5=1. Т.е., когда х=0, у=0 или 1, а когда х=1, то у=1. В итоге:
х8=0, у8=0
х7=1, у7=1
х6=0, у6=0/1
х5=1, у5=1
х4=0, у4=0/1

х3=1, у3=1
х2=0, у2=0/1
х1=1, у1=1

При х8=0 и у8=0 один вариант набора (k=1)
При х7=1 и у7=1 количество вариантов остается неизменным (k=1)
При х6=0, у6 принимает два значения, т.е. количество вариантов удваивается, (k=1*2=2)
При х5=1 и у5=1 количество вариантов остается неизменным (k=2)
При х4=0 и у4=0/1, k=2*2=4, при х3=1, у3=1, k=4, при х2=0, у2=0/1, k=4*2=8, при х1=1, у1=1, k=8.
Получаем, что на первом этапе (х8=0 и у8=0) восемь вариантов.

8

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:

Второй этап, т.е. х8=0, у8=1
Рассмотрим (x7 \/ x8) /\ (¬x7 \/ y7) = 1, т.к. х8=0, х7 должен равняться 1.
Дальше заполняется по аналогии, т.е….
Рассмотрим еще раз (x7 \/ x8) /\ (¬x7 \/ y7) = 1. При х7=1, у7 должен равняться 1, иначе будет 0.
Рассмотрим (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1. При х6=0, у6 может принимать два значения, 0 и 1.
Получаем, что при х=0, у принимает два значения, а при х=1, лишь одно.
Подсчитаем количество вариантов. Также, как и на первом этапе, вариантов будет 8.

0

1

0

1

0

1

0

1

8

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:

Третий этап, т.е. х8=1, у8=1
Рассмотрим (x7 \/ x8) /\ (¬x7 \/ y7) = 1. При х8=1, у может иметь два значения, 0 и 1.
Рассмотрим (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1. При х7=0, х6 может быть только 0. А при х7=1, х6=0/1
Рассмотрим (x5 \/ x6) /\ ((x5 /\ x6) → x7) /\ (¬x5 \/ y5) = 1. При х6=1, по логике х5 может принимать два значения, но, учитывая импликацию, при х7=0 вторая скобка будет равняться нулю, если х5 будет 1. В итоге, х5=0.
Дальше, по аналогии.

1

0

1

1

0

1

0

→ x3) /\ (¬x1 \/ y1) = 1 (x2 \/

x3) /\ ((x2 /\ x3) → x4) /\ (¬x2 \/ y2) = 1 … (x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (¬x6 \/ y6) = 1 (x7 \/ x8) /\ (¬x7 \/ y7) = 1 (¬x8 \/ y8) = 1

Решение:

Как и на первом и втором этапах, если х=0, то у принимает два значения, 0 и 1.
Когда 0, количество вариантов умножаем на два, когда 1, не меняем.
Смотрим первую строчку. 1*2=2, далее не меняем. Потом 2*2=4 и т.д. Получаем 16 вариантов.
Дальше аналогично.
Суммируем.
Все наборы: 8+8+45=61

1

0

1

1

0

1

0

Наборы:
0,0 – 8
0,1 – 8
1,1 –

16

8

8

4

4

2

2

1

45

45

Ответ: 61

наборов значений логических переменных x1, x2, … x9, x10,

которые удовлетворяют всем перечисленным ниже условиям? ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬(x1 ↔ x3) \/ ¬(x2 ↔ x4)) = 1 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬(x2 ↔ x4) \/ ¬(x5 ↔ x7)) = 1 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬(x5 ↔ x7) \/ ¬(x6 ↔ x8)) = 1 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬(x6 ↔ x8) \/ ¬(x9 ↔ x10)) = 1 В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x9, x10, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Решение:
Построим таблицу истинности для первого уравнения
Обозначим через переменные:
a = x1 ↔ x3
b = x2 ↔ x4
с = (x1 ↔ x3) \/ (x2 ↔ x4)
d = ¬(x1 ↔ x3)
e = ¬(x2 ↔ x4)
f = ¬(x1 ↔ x3) \/ ¬(x2 ↔ x4)
g = ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬(x1 ↔ x3) \/ ¬(x2 ↔ x4))

\/ (x2 ↔ x4)) /\ (¬(x1 ↔ x3) \/

¬(x2 ↔ x4)) = 1 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬(x2 ↔ x4) \/ ¬(x5 ↔ x7)) = 1 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬(x5 ↔ x7) \/ ¬(x6 ↔ x8)) = 1 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬(x6 ↔ x8) \/ ¬(x9 ↔ x10)) = 1

Решение:
Из таблицы видно, что нашему условию удовлетворяют 8 строк.
Во втором уравнении присутствуют две переменные x2 и x4, которые есть в первом. Рассмотрим эти столбцы.
Как видно, комбинация каждой пары встречается два раза, т.е. х2=0 и х4=0 (3 и 9 строка) и т.д.
Учитывая эти столбцы и новые переменные х5 и х7, построим новую таблицу для второго уравнения.

\/ (x2 ↔ x4)) /\ (¬(x1 ↔ x3) \/

¬(x2 ↔ x4)) = 1 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬(x2 ↔ x4) \/ ¬(x5 ↔ x7)) = 1 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬(x5 ↔ x7) \/ ¬(x6 ↔ x8)) = 1 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬(x6 ↔ x8) \/ ¬(x9 ↔ x10)) = 1

Решение:
Учитывая эти столбцы и новые переменные х5 и х7, построим новую таблицу для второго уравнения.
Достаточно записать только одну комбинацию для
0;0
0;1
1;0
1;1
Таблица будет такая же, строк также 8.
Т.к. таких комбинаций по две, то количество строк будет 8*2=16
Аналогично, после третьего уравнения: 16*2=32
После четвертого: 32*2=64

Ответ: 64

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → ((x6 ↔ x8) /\ (x9 ↔ x10)) = 1

Решение:
Применим закон де Моргана ¬(A /\ B) = ¬A \/ ¬ B:
¬((x1 ↔ x3) /\ (x2 ↔ x4)) = ¬ (x1 ↔ x3) \/ ¬ (x2 ↔ x4)
По сути, получим тоже уравнение, но в конце 0.
Опираясь на предыдущее задание, можно сделать вывод, что количество наборов также было бы 64, если бы в данном примере было первые 4 уравнения.
Рассмотрим комбинацию х1=0, х2=0, х3=0, х4=0
В этом случае должна быть такая же комбинация и для х6, х8, х9 и х10, иначе условие выполнятся не будет.

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → ((x6 ↔ x8) /\ (x9 ↔ x10)) = 1

Решение:
Для х1=0, х2=0, х3=0, х4=0
Обозначим через новые переменные:
а = x1 ↔ x3
b = x2 ↔ x4
c = (x1 ↔ x3) → (x2 ↔ x4)
d = x6 ↔ x8
e = x9 ↔ x10
f = (x6 ↔ x8) \/ (x9 ↔ x10)
g = (x1 ↔ x3) → (x2 ↔ x4)) → ((x6 ↔ x8) \/ (x9 ↔ x10)

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → ((x6 ↔ x8) /\ (x9 ↔ x10)) = 1

Решение:
Вспоминая предыдущую таблицу, выясняем, что нас не удовлетворяют следующие комбинации (первые четыре уравнения не будут выполняться):
х6=0, х8=0, х9=0, х10=1
х6=0, х8=0, х9=1, х10=0
х6=0, х8=1, х9=0, х10=0
х6=0, х8=1, х9=1, х10=1
х6=1, х8=0, х9=0, х10=0
х6=1, х8=0, х9=1, х10=1
х6=1, х8=1, х9=0, х10=1
х6=1, х8=1, х9=1, х10=0
Уберем их
Далее убираем те строки, которые не удовлетворяют пятому уравнению, т.е. = 0

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → ((x6 ↔ x8) /\ (x9 ↔ x10)) = 1

Решение:
Остается 4 варианта для х1=0, х2=0, х3=0, х4=0
Для каждого последующего набора также по 4 варианта:
х1=0, х2=0, х3=1, х4=1
х1=0, х2=1, х3=0, х4=1
х1=0, х2=1, х3=1, х4=0
х1=1, х2=0, х3=0, х4=1
х1=1, х2=0, х3=1, х4=0
х1=1, х2=1, х3=0, х4=0
х1=1, х2=1, х3=1, х4=1
В итоге:
4*8=32

Ответ: 32

x4
c = (x1 ↔ x3) \/ (x2 ↔ x4)
d

= (x1 ↔ x3) /\ (x2 ↔ x4)
e = ¬((x1 ↔ x3) /\ (x2 ↔ x4)
f = ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4)))
Восемь строк удовлетворяют условию.

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

новая переменная х5. Большая скобка должна равняться 1, а

х5=0.
а = x1 ↔ x3
b = x2 ↔ x4
с = (x1 ↔ x3) → (x2 ↔ x4)
d = ((x1 ↔ x3) → (x2 ↔ x4)) → x5
Остается 8 строк

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

новая переменная х7.
а = x2 ↔ x4
b =

x5 ↔ x7
с = (x2 ↔ x4) \/ (x2 ↔ x4)
d = (x2 ↔ x4) /\ (x2 ↔ x4)
e = ¬((x2 ↔ x4) /\ (x5 ↔ x7))
f = ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7)))
Подходят 8 строк.
Далее сравниваем второе и третье уравнение. Добавляются новые переменные х6 и х8.
Выделим из этой таблицы столбцы х5 и х7
Видно, что комбинация чисел 0;0 и 0;1 повторяется 4 раза

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

будет повторяться 4 раза
а = x5 ↔ x7
b =

x6 ↔ x8
с = (x5 ↔ x7) \/ (x6 ↔ x8)
d = (x5 ↔ x7) /\ (x6 ↔ x8)
e = ¬((x5 ↔ x7) /\ (x6 ↔ x8)))
f = ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8)))
Удовлетворяют условию 4 строчки:
4*4=16 строк
Далее сравниваем третье и шестое уравнение. Добавляется новая переменные х10.

4 раза

4 раза

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

x5 ↔ x7
b = x6 ↔ x8
с = (x5

↔ x7) → (x6 ↔ x8)
d = ((x5 ↔ x7) → (x6 ↔ x8)) → x10
Остается 4*4=16 строк.
Далее будем сравнивать шестую и четвертую строки.
Добавляется новая переменная х9.
Составим новую таблицу, учитывая только выделенные строки, и не рассматривая х5 и х7 (их нет в четвертой)

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

4 раза

4 раза

x10
c = (x6 ↔ x8) \/ (x9 ↔ x10)
d

= (x6 ↔ x8) /\ (x9 ↔ x10)
e = ¬((x6 ↔ x8) /\ (x9 ↔ x10))
f = ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10)))
Удовлетворяют 4 строчки.
4*4=16

23 (Из ФИПИ-2015. Вариант 3). ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0 ((x5 ↔ x7) → (x6 ↔ x8)) → x10 = 0

4 раза

4 раза

Ответ: 16

\/ (x3 ↔ x4)) /\ (¬((x1 ↔ x2) →

(x3 ↔ x4))) = 1 ((x5 ↔ x6) \/ (x7 ↔ x8)) /\ (¬((x5 ↔ x6) → (x7 ↔ x8))) = 1 ((x1 ↔ x2) \/ (x7 ↔ x8)) /\ (¬((x1 ↔ x2) → (x7 ↔ x8))) = 1 ((x3 ↔ x4) → (x9 ↔ x10) = 1

Решение:
а = x1 ↔ x2
b = x3 ↔ x4
c = (x1 ↔ x2) \/ (x3 ↔ x4)
d = (x1 ↔ x2) → (x3 ↔ x4)
e = ¬ ((x1 ↔ x2) → (x3 ↔ x4))
f = ((x1 ↔ x2) \/ (x3 ↔ x4)) /\ (¬((x1 ↔ x2) → (x3 ↔ x4)))
Первое уравнение не связано со вторым, но связано с третьим. Повторяются переменные х1 и х2.
Из таблицы видно, что комбинация х1=0 и х2=0 встречается два раза, и комбинация х1=1 и х2=1 также встречается два раза.
4 строки

\/ (x3 ↔ x4)) /\ (¬((x1 ↔ x2) →

(x3 ↔ x4))) = 1 ((x5 ↔ x6) \/ (x7 ↔ x8)) /\ (¬((x5 ↔ x6) → (x7 ↔ x8))) = 1 ((x1 ↔ x2) \/ (x7 ↔ x8)) /\ (¬((x1 ↔ x2) → (x7 ↔ x8))) = 1 ((x3 ↔ x4) → (x9 ↔ x10) = 1

2 раза

Второе уравнение связано со вторым. Комбинация переменных х7=0, х8=1 и х7=1, х8=0 повторяются уже четыре раза. 4*4=16 строк

Решение:
4 строки. Каждая из них повторяется два раза:
4*2=8 строк

2 раза

4 раза

4 раза

\/ (x3 ↔ x4)) /\ (¬((x1 ↔ x2) →

(x3 ↔ x4))) = 1 ((x5 ↔ x6) \/ (x7 ↔ x8)) /\ (¬((x5 ↔ x6) → (x7 ↔ x8))) = 1 ((x1 ↔ x2) \/ (x7 ↔ x8)) /\ (¬((x1 ↔ x2) → (x7 ↔ x8))) = 1 ((x3 ↔ x4) → (x9 ↔ x10) = 1

Решение:
Четвертое уравнение связано с первым.
Обозначим:
а = x3 ↔ x4
b = x9 ↔ x10
c = (x3 ↔ x4) → (x9 ↔ x10)
Комбинация переменных х3=0, х4=1 и х3=1, х4=0 повторяются уже восемь раз. 8*8=64 строк.

8 раз

8 раз

Ответ: 64

\/ (x3 ↔ x4)) /\ (¬((x1 ↔ x2) →

(x3 ↔ x4))) = 1 ((x5 ↔ x6) \/ (x7 ↔ x8)) /\ (¬((x5 ↔ x6) → (x7 ↔ x8))) = 1 ((x1 ↔ x2) \/ (x7 ↔ x8)) /\ (¬((x1 ↔ x2) → (x7 ↔ x8))) = 1 ((x5 ↔ x6) \/ (x3 ↔ x4)) /\ (¬((x5 ↔ x6) → (x3 ↔ x4))) = 1 x9 ↔ x10 = 1

Решение:
Из предыдущего задания выяснили, что после трех первых уравнений получается 4*4=16 наборов
В этом примере имеется подобное 4 уравнение:
4*8=32
Пятое уравнение:
Две комбинации удовлетворяют условию х9=0, х10=0 и х9=1, х10=1, т.е. количество не поменяется, т.к. до этого также переменные шли по две комбинации.

Ответ: 32

\/ (x4 ↔ x5)) /\ (¬((x2 ↔ x3) →

(x4 ↔ x5))) = 1 ((x6 ↔ x7) \/ (x8 ↔ x9)) /\ (¬((x6 ↔ x7) → (x8 ↔ x9))) = 1 ((x2 ↔ x3) \/ (x8 ↔ x9)) /\ (¬((x2 ↔ x3) → (x8 ↔ x9))) = 1 ((x6 ↔ x7) \/ (x4 ↔ x5)) /\ (¬((x6 ↔ x7) → (x4 ↔ x5))) = 1 (x10 ↔ x1) /\ x1 = 1

Решение:
Ситуация похожая, другие переменные, но это сути не меняет. После четырех уравнений будет 4*8=32 набора.
Пятое уравнение:
Существует только один набор х1=1, х10=1, при котором уравнение будет равняться 1. Количество наборов уменьшается в два раза:
32/2=16

Ответ: 16

\/ (x4 ↔ x5)) \/ ((x2 ↔ x3) →

(x4 ↔ x5)) = 0 (¬(x6 ↔ x7) \/ (x8 ↔ x9)) \/ ((x6 ↔ x7) → (x8 ↔ x9)) = 0 (¬(x2 ↔ x3) \/ (x8 ↔ x9)) \/ ((x2 ↔ x3) → (x8 ↔ x9)) = 0 (¬(x6 ↔ x7) \/ (x4 ↔ x5)) \/ ((x6 ↔ x7) → (x4 ↔ x5)) = 0 (x10 ↔ x1) \/ x1 = 0

Решение:
а = x2 ↔ x3
b = ¬(x2 ↔ x3)
c = x4 ↔ x5
d = ¬ (x2 ↔ x3) \/ (x4 ↔ x5)
e = (x2 ↔ x3) → (x4 ↔ x5)
f = (¬(x2 ↔ x3) \/ (x4 ↔ x5)) \/ ((x2 ↔ x3) → (x4 ↔ x5))
Удовлетворяют 4 строчки. Первое уравнение связано с третьим переменными х2 и х3 (комбинация 0;0 и 1;1, повторятся 2 раза)
Получится, по сути, такая же таблица, но с другими первоначальными переменными: 4*2=8 строк
Далее: 4*4=16 строк
Потом, после 4 уравнений: 4*8=32 строки

\/ (x4 ↔ x5)) \/ ((x2 ↔ x3) →

(x4 ↔ x5)) = 0 (¬(x6 ↔ x7) \/ (x8 ↔ x9)) \/ ((x6 ↔ x7) → (x8 ↔ x9)) = 0 (¬(x2 ↔ x3) \/ (x8 ↔ x9)) \/ ((x2 ↔ x3) → (x8 ↔ x9)) = 0 (¬(x6 ↔ x7) \/ (x4 ↔ x5)) \/ ((x6 ↔ x7) → (x4 ↔ x5)) = 0 (x10 ↔ x1) \/ x1 = 0

Решение:
Рассмотрим пятое уравнение.
х1 обязательно должен равняться 0, а х10=1, иначе это уравнение будет равняться 1.
Получается один набор х1=0, х10=1.
Наборов до этого уравнения было по два, в пятом один набор, т.е. количество комбинаций уменьшается в два раза:
32/2=16

Ответ: 16

\/ (x4 ↔ x5)) \/ ((x2 ↔ x3) →

(x4 ↔ x5)) = 0 (¬(x6 ↔ x7) \/ (x8 ↔ x9)) \/ ((x6 ↔ x7) → (x8 ↔ x9)) = 0 (¬(x2 ↔ x3) \/ (x8 ↔ x9)) \/ ((x2 ↔ x3) → (x8 ↔ x9)) = 0 (¬(x6 ↔ x7) \/ (x4 ↔ x5)) \/ ((x6 ↔ x7) → (x4 ↔ x5)) = 0 (x10 ↔ x1) \/ x1 = 1

Решение:
Опираясь на предыдущий номер, после 4 уравнений будет:
32 набора
Рассмотрим пятое уравнение.
Возможные наборы зависят от х1.
Если х1=0, то х10=0,
если х1=1, то х10 может быть 0, так и 1.
В подобных случаях, количество наборов увеличивается в 1,5 раза:
32*1,5=48

Ответ: 48

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0

Решение:
a = x1 ↔ x3
b = x2 ↔ x4
c = (x1 ↔ x3) \/ (x2 ↔ x4)
d = (x1 ↔ x3) /\ (x2 ↔ x4)
e = ¬((x1 ↔ x3) /\ (x2 ↔ x4)
f = ((x1 ↔ x3) \/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\ (x2 ↔ x4)))
Восемь строк удовлетворяют условию.

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0

Решение:
Рассмотрим первое и пятое уравнение. В пятом добавляется новая переменная х5. Большая скобка должна равняться 1, а х5=0.
а = x1 ↔ x3
b = x2 ↔ x4
с = (x1 ↔ x3) → (x2 ↔ x4)
d = ((x1 ↔ x3) → (x2 ↔ x4)) → x5
Остается 8 строк

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0

Решение:
Рассмотрим пятое и второе уравнение. Во втором добавляется новая переменная х7.
а = x2 ↔ x4
b = x5 ↔ x7
с = (x2 ↔ x4) \/ (x2 ↔ x4)
d = (x2 ↔ x4) /\ (x2 ↔ x4)
e = ¬((x2 ↔ x4) /\ (x5 ↔ x7))
f = ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7)))
Подходят 8 строк.
Далее сравниваем второе и третье уравнение. Добавляются новые переменные х6 и х8.
Выделим из этой таблицы столбцы х5 и х7
Видно, что комбинация чисел 0;0 и 0;1 повторяется 4 раза

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0

Решение:
Построим таблицу. Достаточно записать только одну комбинацию, она будет повторяться 4 раза
а = x5 ↔ x7
b = x6 ↔ x8
с = (x5 ↔ x7) \/ (x6 ↔ x8)
d = (x5 ↔ x7) /\ (x6 ↔ x8)
e = ¬((x5 ↔ x7) /\ (x6 ↔ x8)))
f = ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8)))
Удовлетворяют условию 4 строчки:
4*4=16 строк
Далее сравниваем третье и четвертое уравнение. Добавляются новые переменные х9 и х10.
Выделим из этой таблицы столбцы х6 и х8
Видно, что комбинация чисел 0;0 и 1;1 повторяется 2 раза

4 раза

4 раза

\/ (x2 ↔ x4)) /\ (¬((x1 ↔ x3) /\

(x2 ↔ x4))) = 0 ((x2 ↔ x4) \/ (x5 ↔ x7)) /\ (¬((x2 ↔ x4) /\ (x5 ↔ x7))) = 0 ((x5 ↔ x7) \/ (x6 ↔ x8)) /\ (¬((x5 ↔ x7) /\ (x6 ↔ x8))) = 0 ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10))) = 0 ((x1 ↔ x3) → (x2 ↔ x4)) → x5 = 0

Решение:
Построим таблицу. Достаточно записать только одну комбинацию, она будет повторяться 8 раз
а = x6 ↔ x8
b = x9 ↔ x10
с = (x6 ↔ x8) \/ (x9 ↔ x10)
d = (x6 ↔ x8) /\ (x9 ↔ x10)
e = ¬((x6 ↔ x8) /\ (x9 ↔ x10)))
f = ((x6 ↔ x8) \/ (x9 ↔ x10)) /\ (¬((x6 ↔ x8) /\ (x9 ↔ x10)))
Удовлетворяют условию 4 строчки:
4*8=32 строки

8 раз

8 раз

Ответ: 32

целых чисел (некоторые числа могут быть одинаковыми). Нужно написать

программу, которая выводит на экран количество нечётных чисел в исходной последовательности и максимальное нечётное число. Если нечётных чисел нет, требуется на экран вывести «NO». Известно, что вводимые числа не превышают 1000. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе последовательности: 2 9 4 3
2. Приведите пример такой последовательности, содержащей хотя бы одно
нечётное число, что, несмотря на ошибки, программа печатает правильный ответ.
3. Найдите все ошибки в этой программе (их может быть одна или несколько). Известно, что каждая ошибка затрагивает только одну строку и может быть исправлена без изменения других строк.
Для каждой ошибки:
1) выпишите строку, в которой сделана ошибка;
2) укажите, как исправить ошибку, т.е. приведите правильный вариант строки.
Достаточно указать ошибки и способ их исправления для одного языка
программирования.
Обратите внимание, что требуется найти ошибки в имеющейся программе, а не написать свою, возможно, использующую другой алгоритм решения.
Исправление ошибки должно затрагивать только строку, в которой находится
ошибка.

Есть логические, т.е. некорректный алгоритм.
1) В цикле for запрашивается

первое число 2. Оно четное, условие не выполняется и ничего не происходит.
Дальше рассматривается 9, оно нечетное, count увеличивается на 1; условие 9>999 не выполняется, переменная maximum не меняется.
Потом смотрим число 4. Аналогично с 2, ничего не происходит.
Число 3. Нечетное, count = 2; условие 3>999 не выполняется, переменная maximum не меняется.
Следующее условие, count>0, да, печатается в начале 2, а потом 999.
Очевидно, это не верно выполненная программа. Должно выводить 2 и 9. Но нам требовалось определить, что напечатает программа при данных входных.

24. 1. Напишите, что выведет эта программа при вводе последовательности: 2 9 4 3
2. Приведите пример такой последовательности, содержащей хотя бы одно нечётное число, что, несмотря на ошибки, программа печатает правильный ответ.
3. Найдите все ошибки в этой программе. Известно, что каждая ошибка затрагивает только одну строку и может быть исправлена без изменения других строк.
Для каждой ошибки:
1) выпишите строку, в которой сделана ошибка;
2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

> maximum. Мы сравниваем введенный нечетный х с числом

999. Это условие никогда не выполнится, т.к. максимальное нечетное число и есть 999, а у нас входные данные по условию задачи не превосходят 1000 (четное). Можно внести любые числа, не превосходящие 1000 (обязательно среди них должно быть 999, чтобы вывести это максимальное число). Пусть, для сравнения, среди них будет не одно, а два нечетных числа.
10 26 999 41
Программа выведет в начале число 2 (количество нечетных), а затем 999 (максимальное нечетное число)

24. 1. Напишите, что выведет эта программа при вводе последовательности: 2 9 4 3
2. Приведите пример такой последовательности, содержащей хотя бы одно нечётное число, что, несмотря на ошибки, программа печатает правильный ответ.
3. Найдите все ошибки в этой программе. Известно, что каждая ошибка затрагивает только одну строку и может быть исправлена без изменения других строк.
Для каждой ошибки:
1) выпишите строку, в которой сделана ошибка;
2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

ошибки. Вторую и третью строчку можно и объединить, но

это не ошибка.
Далее count обнуляется, правильно, т.к. до начала введения данных количество нечетных равняется нулю, т.е. их еще нет.
Следующая строка maximum:=999 некорректна. Введенное значение должно быть больше максимального (условие if x>maximum), чтобы дальше выполнялось условие.
Наша цель, в максимуме присвоить такое значение, которое является невозможным для входных данных. У нас числа неотрицательное, т.е. больше 0. Вместо 999 надо указать 0.
maximum:=999 ; maximum:=0;
Дальше. Цикл for, корректно, т.к. надо ввести 4 числа. Потом считываем с клавиатуры введенное число.
Затем проверка нечетности. Верно.
Счетчик count увеличивается на один. Все верно.

24. 3. Найдите все ошибки в этой программе. Известно, что каждая ошибка затрагивает только одну строку и может быть исправлена без изменения других строк.
Для каждой ошибки:
1) выпишите строку, в которой сделана ошибка;
2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Далее проверяем условие, учитывая, что maximum:=0; . Все корректно.
Дальше переменной maximum должны присвоить текущее значение. А здесь присваивается счетчик. Это не верно.
maximum:=i; maximum:=x;
Далее проверяется if count > 0 и печатается количество нечетных и максимальное из них. Иначе печатается слово NO. Ошибок нет.

последовательность из четырёх неотрицательных целых чисел (некоторые числа могут

быть одинаковыми). Нужно написать программу, которая выводит на экран количество чисел, кратных 3 в исходной последовательности и минимальное кратное 3 число. Если таких чисел нет, требуется на экран вывести «NO». Известно, что вводимые числа не превышают 1000. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе последовательности: 6 9 12 5
2. Приведите пример такой последовательности, содержащей хотя бы одно кратное 3 число, что, несмотря на ошибки, программа печатает правильный ответ.
3. Найдите все ошибки в этой программе (их может быть одна или несколько).
Примечание: 0 – кратное 3 число.

Решение: 1) x mod 3 = 0, 6 mod 3 = 0, да, count:= count + 1 = 0 + 1 = 1, x < 0, 6 < 0, нет;
x mod 3 = 0, 9 mod 3 = 0, да, count:= count + 1 = 1 + 1 = 2, x < 0, 9 < 0, нет;
x mod 3 = 0, 12 mod 3 = 0, да, count:= count + 1 = 2 + 1 = 3, x < 0, 12 < 0, нет;
x mod 3 = 0, 5 mod 3 = 0, нет, count:= 3, x < 0, 5 < 0, нет;
Печатается 3 и 0 (а должно 3 и 6).
2) 0 7 15 6
x mod 3 = 0, 0 mod 3 = 0, да, count:= count + 1 = 0 + 1 = 1, x < 0, 6 < 0, нет;
x mod 3 = 0, 7 mod 3 = 0, нет, count:= 1, x < 0, 7 < 0, нет;
x mod 3 = 0, 15 mod 3 = 0, да, count:= count + 1 = 1 + 1 = 2, x < 0, 15 < 0, нет;
x mod 3 = 0, 6 mod 3 = 0, да, count:= count + 1 = 2 + 1 = 3, x < 0, 6 < 0, нет;
Печатается 3 и 0 (а должно 3 и 6).
3) Ошибка minimum:= 0; исправить на minimum:= 999;
minimum:= i; исправить на minimum:= х;

последовательность из четырёх неотрицательных целых чисел (некоторые числа могут

быть одинаковыми). Нужно написать программу, которая выводит на экран количество чисел, кратных 11 в исходной последовательности и сумму таких чисел. Если таких чисел нет, требуется на экран вывести «NO». Известно, что вводимые числа не превышают 1000. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе последовательности: 22 33 65 45
2. Приведите пример такой последовательности, содержащей хотя бы одно кратное 11 число, что, несмотря на ошибки, программа печатает правильный ответ.
3. Найдите все ошибки в этой программе (их может быть одна или несколько).
Примечание: 0 – делится на любое целое число.

Решение: 1) x mod 11 = 0, 22 mod 11 = 0, да, count:= count + 1 = 0 + 1 = 1, sum:=22;
x mod 11 = 0, 33 mod 11 = 0, да, count:= count + 1 = 1 + 1 = 2, sum:=33;
x mod 11 = 0, 65 mod 11 = 0, нет, count:= 2;
x mod 11 = 0, 45 mod 11 = 0, нет, count:= 2;
Печатается 2 и 33 (а должно 2 и 55).
2) 77 12 15 60
x mod 11 = 0, 77 mod 11 = 0, да, count:= count + 1 = 0 + 1 = 1, sum:=77;
x mod 11 = 0, 12 mod 11 = 0, нет, count:= 1;
x mod 11 = 0, 15 mod 11 = 0, нет, count:= 1;
x mod 11 = 0, 60 mod 11 = 0, нет, count:= 1;
Печатается 1 и 77
3) Ошибка sum:= x; исправить на sum:= sum + x;
sum > 0; исправить на count > 0;

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится минимальная цифра этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 642.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 0, 642 > 0, да, digit:= N div 10 = 642 div 10 = 64;
if digit < min_digit, 64 < 10, нет;
N:= N div 10 = 64 div 10 = 6;
N > 0, 6 > 0, да, digit:= N div 10 = 6 div 10 = 0;
if digit < min_digit, 0 < 10, да, min_digit:= digit = 0;
N:= N div 10 = 6 div 10 = 0;
N > 0, 0 > 0, нет, выходим из цикла и печатаем 0 (а должны 2).
2) Ошибка digit:= N div 10; исправить на digit:= N mod 10; (иначе теряется цифра 2, а она минимальна);
writeln(digit); исправить на writeln(min_digit);

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится максимальная цифра этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 762.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > = 10, 762 > =10, да, digit:= N mod 10 = 762 mod 10 = 2;
if digit < max_digit, 2 < 0, нет;
N:= N div 10 = 762 div 10 = 76;
N >= 10, 76 >= 10, да, digit:= N mod 10 = 76 mod 10 = 6;
if digit < max_digit, 6 < 0, нет;
N:= N div 10 = 76 div 10 = 7;
N >= 10, 7 >= 10, нет, выходим из цикла и печатаем 0 (а должны 7).
2) Ошибка while N > =10; исправить на while N > =1; или while N >0; (иначе не проверяется и теряется первая цифра 7, а она максимальна);
if digit < max_digit then исправить на if digit > max_digit then

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится максимальная цифра этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 384.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 0, 384 > 0, да, digit:= N mod 10 = 384 mod 10 = 4;
if digit > max_digit, 4 > 9, нет;
N:= N div 10 = 384 div 10 = 38;
N > 0, 38 > 0, да, digit:= N mod 10 = 38 mod 10 = 8;
if digit > max_digit, 8 > 9, нет;
N:= N div 10 = 38 div 10 = 3;
N > 0, 3 > 0, да, digit:= N mod 10 = 3 mod 10 = 3;
if digit > max_digit, 3 > 9, нет;
N:= N div 10 = 3 div 10 = 0;
N > 0, 0 > 0, нет, выходим из цикла и печатаем 9 (а должны 8).
2) Ошибка max_digit :=9; исправить на max_digit :=1; или max_digit :=0; (иначе условие if digit > max_digit не будет выполняться);
digit := max_digit ; исправить на max_digit := digit;

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится максимальная цифра этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 673.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 0, 673 > 0, да, digit:= N div 10 = 673 div 10 = 67;
if digit > max_digit, 67 > 0, да, max_digit:=digit = 67;
N:= N div 10 = 673 div 10 = 67;
N > 0, 67 > 0, да, digit:= N div 10 = 67 div 10 = 6;
if digit > max_digit, 6 > 67, нет;
N:= N div 10 = 67 div 10 = 6;
N > 0, 6 > 0, да, digit:= N div 10 = 6 div 10 = 0;
if digit > max_digit, 0 > 0, нет;
N:= N div 10 = 6 div 10 = 0;
N > 0, 0 > 0, нет, выходим из цикла и печатаем 0 (а должны 7).
2) Ошибка digit:= N div 10; исправить на digit:= N mod 10; (иначе теряется цифра 3, а она минимальна);
writeln(digit); исправить на writeln(max_digit);

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится произведение цифр этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 133.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 0, 133 > 0, да, digit:= N mod 10 = 133 mod 10 = 3;
product:= product + digit = 0 + 3 = 3;
N:= N div 10 = 133 div 10 = 13;
N > 0, 13 > 0, да, digit:= N mod 10 = 13 mod 10 = 3;
product:= product + digit = 3 + 3 = 6;
N:= N div 10 = 13 div 10 = 1;
N > 0, 1 > 0, да, digit:= N mod 10 = 1 mod 10 = 1;
product:= product + digit = 6 + 1 = 7;
N:= N div 10 = 1 div 10 = 0;
N > 0, 0 > 0, нет, выходим из цикла и печатаем 7 (а должны 9).
2) Ошибка product:= 0; исправить на product:= 1; (иначе при произведении будет получаться всегда 0);
product:= product + digit; исправить на product:= product * digit;

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится произведение цифр этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 325.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 0, 325 > 0, да, digit:= N mod 10 = 325 mod 10 = 5;
digit := product * digit = 1 * 5 = 5;
N:= N div 10 = 325 div 10 = 32;
N > 0, 32 > 0, да, digit:= N mod 10 = 32 mod 10 = 2;
digit := product * digit = 1 * 2 = 2;
N:= N div 10 = 32 div 10 = 3;
N > 0, 3 > 0, да, digit:= N mod 10 = 3 mod 10 = 3;
digit := product * digit = 1 * 3 = 3;
N:= N div 10 = 3 div 10 = 0;
N > 0, 0 > 0, нет, выходим из цикла и печатаем 3 (а должны 30).
2) Ошибка digit := product * digit; исправить на product := product * digit;
writeln(digit); исправить на writeln(product);

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится сумма цифр этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 13.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N > 1, 13 > 1, да, digit:= N mod 10 = 13 mod 10 = 3;
sum:= sum + digit = 0 + 3 = 3;
N:= N – 10 = 13 – 10 = 3;
N > 1, 3 > 1, да, digit:= N mod 10 = 3 mod 10 = 3;
sum:= sum + digit = 3 + 3 = 6;
N:= N – 10 = 3 – 10 = – 7;
N > 1, – 7 > 1, нет, выходим из цикла и печатаем 6 (а должны 4).
2) Ошибка while N > 1; исправить на while N > 0;(иначе не будет использоваться цифра 1);
N:= N – 10; исправить на N:= N div 10;

при выполнении, которой с клавиатуры считывается натуральное число N,

не превосходящее 109 , и выводится сумма цифр этого числа. Программист написал программу неправильно.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 342.
2. Найдите все ошибки в этой программе (их может быть одна или несколько).
Для каждой ошибки: 1) выпишите строку, в которой сделана ошибка; 2) укажите, как исправить ошибку.
Исправление ошибки должно затрагивать только строку, в которой находится ошибка.

Решение:
1) N >= 1, 342 > =1, да, digit:= N mod 10 = 342 mod 10 = 2;
sum:= digit = 2;
N:= N div 10 = 342 div 10 = 34;
N >= 1, 34 > =1, да, digit:= N mod 10 = 34 mod 10 = 4;
sum:= digit = 4;
N:= N div 10 = 34 div 10 = 3;
N >= 1, 3 > =1, да, digit:= N mod 10 = 3 mod 10 = 3;
sum:= digit = 3;
N:= N div 10 = 3 div 10 = 0;
N >= 1, 0 >=1, нет, выходим из цикла и печатаем 3 (а должны 9).
2) Ошибка sum:= digit; исправить на sum:= sum+digit; (иначе не будут суммироваться цифры);
writeln(digit); исправить на writeln(sum);

состоящий из 6 элементов.

25. Дан целочисленный массив из 20

элементов. Элементы массива могут принимать целые значения от –10 000 до10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм позволяющий найти и вывести количество пар элементов массива, сумма которых нечётна и положительна. Под парой подразумевается два подряд идущих элемента массива. Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

Сложим соседние, т.е. 1 и 2, 2 и 3 и т.д. По условию, сумма должна быть положительной и нечетной.
1) 6 + (-4) = 2 – не подходит
2) -4 + 9 = 5 – подходит
3) 9 + 5 = 14 – не подходит
4) 5 + 6 = 11 – подходит
5) 6 + (-9) = - 3 – не подходит
В итоге, ответом для этих входных данных будет число 2.

будет отвечать за количество пар, удовлетворяющие условию задачи. Для

начала ее обнулим, т.е. в программе она запишется k:=0;
Далее нужно запустить цикл, в котором будем рассматривать все пары. Счетчиком будет выступать переменная i, которая начинается от второго элемента до N. Т.к. нужно рассматривать текущий элемент и предыдущий.
for i:=2 to N do

25. Количество пар элементов массива, сумма которых нечётна и положительна.

Потом делается проверка условий: сумма двух соседних элементов больше нуля и нечетная.
if (a[i] + a[i-1] > 0) and ((a[i] + a[i-1]) mod 2 = 1) then
Если выполняется данное условие, то увеличиваем счетчик k на единицу
k:= k + 1;
Возможна и следующая запись: inc(k)
В конце распечатываем k writeln(k);
Распишем еще раз.

k:=0;
for i:=2 to N do
if (a[i] + a[i-1] > 0) and ((a[i] + a[i-1]) mod 2 = 1) then
k:= k + 1;
writeln(k);

из 30 элементов. Элементы массива могут принимать целые значения

от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести максимальное значение среди трёхзначных элементов массива, не делящихся на 20. Если в исходном массиве нет трёхзначного элемента, не кратного 20, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:
Используем программу Free Pascal 2.4
По условию задачи элементы массива должны быть трехзначными, т.е. a[i]>99, соответственно, чтобы это условие выполнялось первоначальная переменная max должна равняться 99 (max:=99;)
Дальше вводим цикл с счетчиком i (for i:=1 to N do)
Потом вводим условия: трехзначное число, не кратно 20 и больше max
(if (a[i]>=100) and (a[i]<=999) and (a[i] mod 20<>0) and (a[i]>max) then)
Присваиваем подходящий элемент для переменной max (max:=a[i];)
Далее, новое условие, если эта переменная больше 99, то выводим ее на экран, если нет, выводим текст Не найдено
(if max>99 then writeln(max) else writeln(‘Не найдено’);)

из 30 элементов. Элементы массива могут принимать целые значения

от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести максимальное значение среди трёхзначных элементов массива, не делящихся на 20. Если в исходном массиве нет трёхзначного элемента, не кратного 20, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:
Запишем еще раз часть программы

max:=99;
for i:=1 to N do
if (a[i]>=100) and (a[i]<=999) and (a[i] mod 20<>0) and (a[i]>max) then
max:=a[i];
if max>99 then writeln(max) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести минимальное значение среди трёхзначных элементов массива, не делящихся на 20. Если в исходном массиве нет трёхзначного элемента, не кратного 20, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

min:=1000;
for i:=1 to N do
if (a[i]>=100) and (a[i]<=999) and (a[i] mod 20<>0) and (a[i]min:=a[i];
if min<1000 then writeln(min) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от -1000 до 1000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести минимальное значение среди положительных элементов массива, оканчивающихся на 5. Если в исходном массиве нет элемента, значение которого положительно и оканчивается цифрой 5, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

min:=1001;
for i:=1 to N do
if (a[i]>0) and (a[i] mod 10=5) and (a[i]min:=a[i];
if min<1001 then writeln(min) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от -1000 до 1000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести минимальное значение среди отрицательных элементов массива, оканчивающихся на 3. Если в исходном массиве нет элемента, значение которого отрицательно и оканчивается цифрой 3, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

min:=0;
for i:=1 to N do
if (a[i]<0) and ((-1*a[i]) mod 10=3) and (a[i]min:=a[i];
if min<0 then writeln(min) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от -1000 до 1000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести максимальное значение среди отрицательных элементов массива, не оканчивающихся на 3. Если в исходном массиве нет элемента, значение которого отрицательно и не оканчивается цифрой 3, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

max:=-1001;
for i:=1 to N do
if (a[i]<0) and ((-1*a[i]) mod 10<>3) and (a[i]>max) then
max:=a[i];
if max>-1001 then writeln(max) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести минимальное значение среди трех- и двухзначных элементов массива, делящихся на 10. Если в исходном массиве нет ни трех-, ни двузначного элемента, кратного 10, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

min:=1000;
for i:=1 to N do
if (a[i]>9) and (a[i]<=999) and(a[i] mod 10=0) and (a[i]min:=a[i];
if min<1000 then writeln(min) else writeln(‘Не найдено’);

из 30 элементов. Элементы массива могут принимать целые значения

от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести максимальное значение среди элементов массива, не являющиеся трехзначными и не делящихся на 20. Если в исходном массиве нет не трехзначного элемента, не кратного 20, то вывести сообщение «Не найдено». Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования и естественного языка. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных. В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

Решение:

max:=-1;
for i:=1 to N do
if ((a[i]<100) or (a[i]>999)) and (a[i] mod 20<>0) and (a[i]>max) then
max:=a[i];
if max>-1 then writeln(max) else writeln(‘Не найдено’);

следующую игру. Перед игроками лежит куча камней. Игроки ходят

по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 18 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 35. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 35 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 34. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающие ходы.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
 Петя не может выиграть за один ход;
 Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную стратегию Пети.
Задание 3. Укажите значение S, при котором одновременно выполняются два условия:
 у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
 у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте,
кто делает ход; в узлах – количество камней в позиции.

34 Петя выиграет в один ход. Ему достаточно увеличить

количество камней в два раза.
б) При S = 17 Петя не сможет выиграть. Он получит либо 18 (через +1), либо 20 (+3), либо 34 (*2). В любом из этих случаев, Ваня увеличит количество камней в два раза и выиграет.
По сути, S=17, это проигрышная ситуация. Как ни ходи, все равно проиграешь.

26. Петя (П) – первый ход, Ваня (В) – второй. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 35 или больше камней. 1 ≤ S ≤ 34
Задание 1. а) Укажите S, при которых Петя может выиграть в один ход.
б) Укажите S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия:
 Петя не может выиграть за один ход;
 Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 3. Укажите значение S, при котором одновременно выполняются два условия:
 у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
 у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Постройте дерево всех партий, возможных при этой выигрышной стратегии.

ситуации, т.е. перед ходом Вани количество камней сделать равным

17. А этого можно добиться при S = 14 (через + 3) и S = 16 (через + 1).

26. Петя (П) – первый ход, Ваня (В) - второй. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 35 или больше камней. 1 ≤ S ≤ 34
Задание 1. а) Укажите S, при которых Петя может выиграть в один ход.
б) Укажите S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия:
 Петя не может выиграть за один ход;
 Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 3. Укажите значение S, при котором одновременно выполняются два условия:
 у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
 у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Постройте дерево всех партий, возможных при этой выигрышной стратегии.

Петю к проигрышной позиции, т.е. к 17, либо к

числу, больше 17. Ваня при этом должен выиграть либо первым ходом, либо вторым. Это получается при S=13. У Пети три варианта, либо сделать 14 (+1), либо 16 (+3), либо 26 (*2). В третьем случае Ваня выиграет, умножив 26 на 2. В первых двух случаях, он приведет Петю к 17 камням в куче (а это поражение Пети). Схематически, это будет выглядеть так:

26. Петя (П) – первый ход, Ваня (В) - второй. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 35 или больше камней. 1 ≤ S ≤ 34
Задание 3. Укажите значение S, при котором одновременно выполняются два условия:
 у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
 у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Постройте дерево всех партий, возможных при этой выигрышной стратегии.

измерения энергии космических лучей. Каждую минуту прибор передаёт по

каналу связи неотрицательное вещественное число – количество энергии, полученной за последнюю минуту, измеренное в условных единицах. Временем, в течение которого происходит передача, можно пренебречь. Необходимо найти в заданной серии показаний прибора минимальное произведение двух показаний, между моментами передачи которых прошло не менее 6 минут. Количество энергии, получаемое прибором за минуту, не превышает 1000 условных единиц. Общее количество показаний прибора в серии не превышает 10 000.
Вам предлагается два задания, связанные с этой задачей: задание А и задание Б. Вы можете решать оба задания А и Б или одно из них по своему выбору.
Итоговая оценка выставляется как максимальная из оценок за задания А и Б. Если решение одного из заданий не представлено, то считается, что оценка за это задание составляет 0 баллов.
Задание Б является усложненным вариантом задания А, оно содержит дополнительные требования к программе.
А. Напишите на любом языке программирования программу для решения поставленной задачи, в которой входные данные будут запоминаться в массиве, после чего будут проверены все возможные пары элементов. Перед программой укажите версию языка программирования.
ОБЯЗАТЕЛЬНО укажите, что программа является решением ЗАДАНИЯ А. Максимальная оценка за выполнение задания А равна 2 баллам.
Б. Напишите программу для решения поставленной задачи, которая будет эффективна как по времени, так и по памяти (или хотя бы по одной из этих характеристик). Программа считается эффективной по времени, если время работы программы пропорционально количеству полученных показаний прибора N, т.е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз. Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта. Перед программой укажите версию языка программирования и кратко опишите использованный алгоритм.
ОБЯЗАТЕЛЬНО укажите, что программа является решением ЗАДАНИЯ Б. Максимальная оценка за правильную программу, эффективную по времени и по памяти, равна 4 баллам.
Максимальная оценка за правильную программу, эффективную по времени, но неэффективную по памяти, равна 3 баллам.
НАПОМИНАЕМ! Не забудьте указать, к какому заданию относится каждая из представленных Вами программ.