- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Основы логики
Содержание
- 3. Высказыванием называется любое повествовательное предложение, про которое известно, что оно или истинно, или ложно.
- 4. Например:Жирафы летят на север. - Ложное высказывание.Треугольник
- 5. Высказывание считается простым, если никакую его часть
- 6. В математической логике высказывания обозначают большими латинскими буквами.Например:А = Москва– столица России.С = Все растения ядовиты.
- 7. Простые высказывания называются логическими переменными Например:А =
- 8. Сложные высказывания называются логическими функциями, а значение
- 9. Составные (сложные) высказывания строятся из простых с
- 10. обозначим ЛОГИЧЕСКИЕ СВЯЗКИ - ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ и получим с их помощью (составные) высказывания
- 11. I. Операция – логическое умножениеОбъединение двух
- 12. Высказывание вида A & B (А конъюнкция
- 13. II. Операция – логическое
- 14. Высказывание вида A V B (А дизъюнкция
- 15. III. Операция – логическое отрицаниеПрисоединение частицы
- 16. Высказывание вида Ā (инверсия А) делает истинное
- 17. IV. Операция – логическое следованиеОбъединение двух
- 18. Высказывание вида A → B (А импликация
- 19. V. Операция – логическое равенствоОбъединение двух
- 20. Высказывание вида A ↔ B (А эквивалентность
- 21. Решение логических выражений через построение таблиц истинности Урок 2:
- 22. Применяя логические операции, мы можем решить любые
- 23. Например:Для определения значения логической функции необходимо помнитьпорядок
- 24. Операции в логическом выражении выполняются слева направо
- 25. Для построения таблицы истинности любой логической функции
- 26. Для построения таблицы истинности любой логической функции
- 27. Количество входных переменных равно трем (X,Y,Z), а
- 28. Определим значение логической функции
- 29. Значение логической функции Подробное решение
- 30. Математическая логика - решение задач Урок 3:
- 31. 1)F= (0 \/ 0) \/ (1 \/
- 32. Для какого из указанных значений числа X
- 33. Скачать презентацию
- 34. Похожие презентации





























Слайд 3
Высказыванием
называется любое повествовательное предложение, про которое известно,
что оно или истинно, или ложно.
Слайд 4
Например:
Жирафы летят на север. - Ложное высказывание.
Треугольник -
это геометрическая фигура. - Истинное высказывание
Число 6 не делится
на 2. - Ложное высказывание.Посмотрите на доску. –
Не высказывание.
Слайд 5 Высказывание считается простым, если никакую его часть нельзя
рассматривать как отдельное высказывание
Высказывание, которое можно разложить на части
называется сложным (составным).
Слайд 6
В математической логике высказывания обозначают большими латинскими буквами.
Например:
А
= Москва– столица России.
С = Все растения ядовиты.
Слайд 7
Простые высказывания называются
логическими переменными
Например:
А = «Луна
является спутником Земли.» → А = 1 В = «Москва
– столица Германии.»→ В = 0
Слайд 8
Сложные высказывания называются логическими функциями,
а значение логической
функции также может принимать значения только 0 или 1.
Слайд 9 Составные (сложные) высказывания строятся из простых с помощью
логических связок:
"и",
"или",
"не",
«если …, то…»,
«…тогда
и только тогда, когда…»и др.
Например
Слайд 10 обозначим ЛОГИЧЕСКИЕ СВЯЗКИ - ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ и получим с их
помощью (составные) высказывания
Слайд 11
I. Операция –
логическое умножение
Объединение двух (или нескольких)
высказываний в одно при помощи союза «и» называется
операцией
логического умножения или конъюнкциейВ алгебре логики конъюнкция обозначается значком «&» либо «Λ»
Слайд 12 Высказывание вида A & B (А конъюнкция B
) истинно тогда и только тогда, когда
истинны оба
высказывания и А и BТаблица истинности для А & В
Слайд 13
II. Операция –
логическое сложение
Объединение двух
(или нескольких) высказываний в одно при помощи союза «или»
называетсяоперацией логического сложения или дизъюнкцией
В алгебре логики дизъюнкция обозначается значком «V» либо «+»
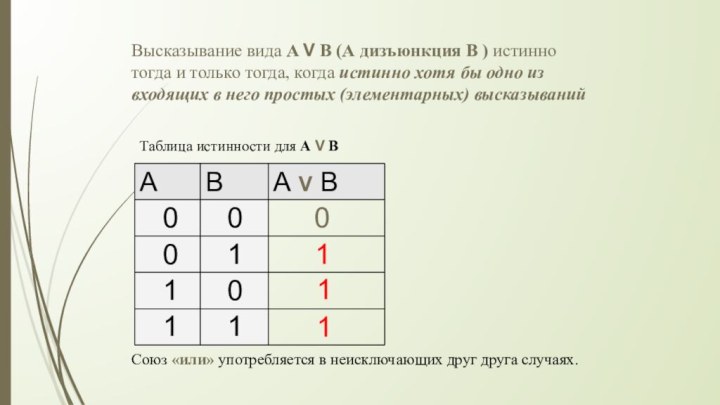
Слайд 14 Высказывание вида A V B (А дизъюнкция B
) истинно тогда и только тогда, когда истинно хотя
бы одно из входящих в него простых (элементарных) высказыванийСоюз «или» употребляется в неисключающих друг друга случаях.
Таблица истинности для А V В
Слайд 15
III. Операция –
логическое отрицание
Присоединение частицы «не» к
высказыванию называется операцией логического отрицания или инверсией
В алгебре логики
инверсия обозначается значком « ¬ » либо чертой над высказыванием «Ā»Рассмотренные выше операции были двуместные, т.е. выполнялись над двумя высказываниями. В алгебре логики широко применяется и одноместная операция – операция отрицание.
Слайд 16 Высказывание вида Ā (инверсия А) делает истинное высказывание
ложным и , наоборот, ложное - истинным
Например
Таблица истинности для
Ā
Слайд 17
IV. Операция –
логическое следование
Объединение двух высказываний с
помощью оборота речи «если …, то …» называется
операцией
логического следования или импликацияВ алгебре логики импликация обозначается значком « → »
Слайд 18 Высказывание вида A → B (А импликация B
) ложно тогда и только тогда,
когда А –
истинно, а B – ложно (т.е. из истинного высказывания следует ложное)Таблица истинности для А → В
Слайд 19
V. Операция –
логическое равенство
Объединение двух высказываний с
помощью оборота речи
«…тогда и только тогда, когда …»
называется
операцией логического равенства или эквивалентность
В алгебре логики эквивалентность обозначается значком « ↔ »
Слайд 20
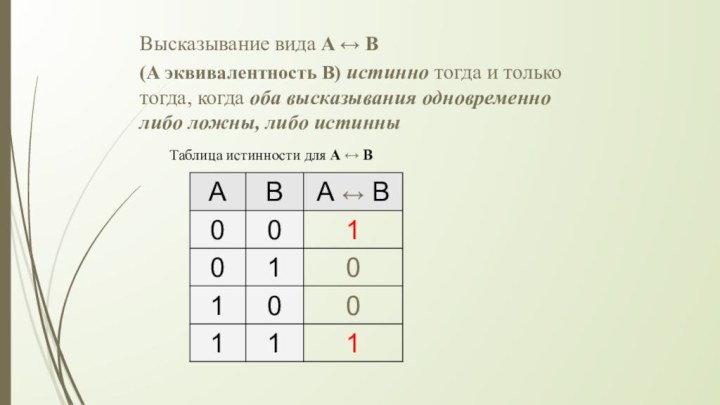
Высказывание вида A ↔ B
(А эквивалентность B)
истинно тогда и только тогда, когда оба высказывания одновременно
либо ложны, либо истинныТаблица истинности для А ↔ В
Слайд 22 Применяя логические операции, мы можем решить любые логические
выражения:
Для этого простые логические высказывания обозначим как логические переменные
– буквами;Свяжем их с помощью знаков логических операций.
Такие формулы в алгебре логики называются логическими выражениями.
Слайд 23
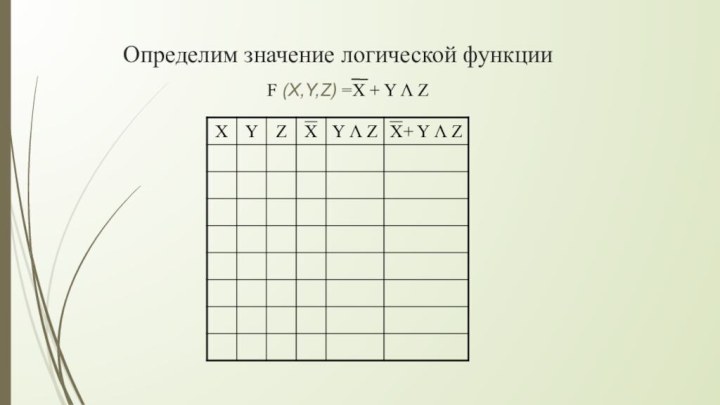
Например:
Для определения значения логической функции
необходимо помнить
порядок выполнения
логических операций по убыванию старшинства
Теперь мы можем определить значение
логической функции для любого набора значений логических переменных.Слайд 24 Операции в логическом выражении выполняются слева направо с
учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4.
импликация; 5. эквивалентность.
Слайд 25
Для построения таблицы истинности любой логической функции
следует
соблюдать:
1. определить кол-во строк таблицы – 2n , где
n = кол-ву логических переменных;2. определить кол-во столбцов таблицы- оно равно кол-ву логических переменных + кол-во логических операций;
Слайд 26
Для построения таблицы истинности любой логической функции
следует
соблюдать:
3. построить таблицу истинности с найденным кол-вом строк и
столбцов + строка с названием столбцов;4. заполнить столбцы таблицы, выполняя логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Слайд 27
Количество входных переменных равно трем (X,Y,Z), а значит
строк
Q= 23 = 8 +1 =9 (заголовки столбцов).
2. Количество столбцов равно 6
(3 переменные + 3 операции).
Вернёмся к нашему примеру:
Слайд 31
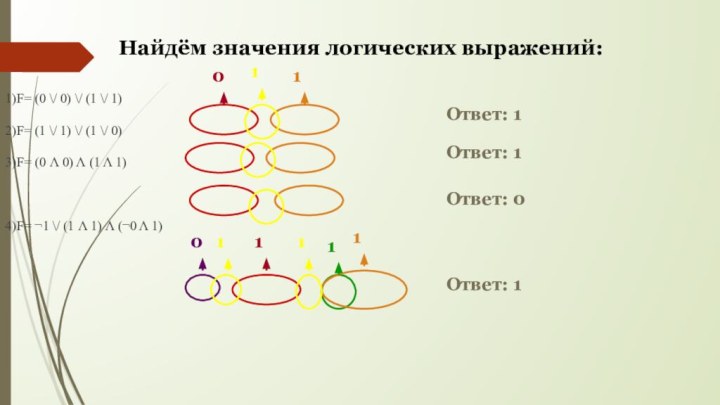
1)F= (0 \/ 0) \/ (1 \/ 1)
2)F=
(1 \/ 1) \/ (1 \/ 0)
3)F= (0 Λ
0) Λ (1 Λ 1) 4)F= ¬1 \/ (1 Λ 1) Λ (¬0 Λ 1)
Найдём значения логических выражений:
0
1
1
1
1
1
0
1
1
Ответ: 1
Ответ: 1
Ответ: 0
Ответ: 1
Слайд 32 Для какого из указанных значений числа X истинно
высказывание ((X > 3) → (X > 4))
Решение:
В
записи логического высказывания стоит отрицание сложного высказывания. Если ((X > 3) –> (X > 4)) = 1 (истинно),
то (X > 3) –> (X > 4) = 0 (ложно)
1) 1 2)2 3) 3 4) 4