Слайд 2
Соедините правильные определения или обозначения:
1. Логика
1. А→В
2. Высказывание 2. Логическое сложение
3. Алгебра логики 3. Наука о формах и способах мышления.
4. Логическая константа 4. Логическое отрицание
5. Дизъюнкция 5. Истина и ложь
6. Инверсия 6. А↔В
7. Конъюнкция 7. &
8. Импликация 8. Наука об операциях над высказываниями
9. Эквивалентность 9. Повествовательное предложение, в
что-либо утверждается или отрицается
Слайд 3
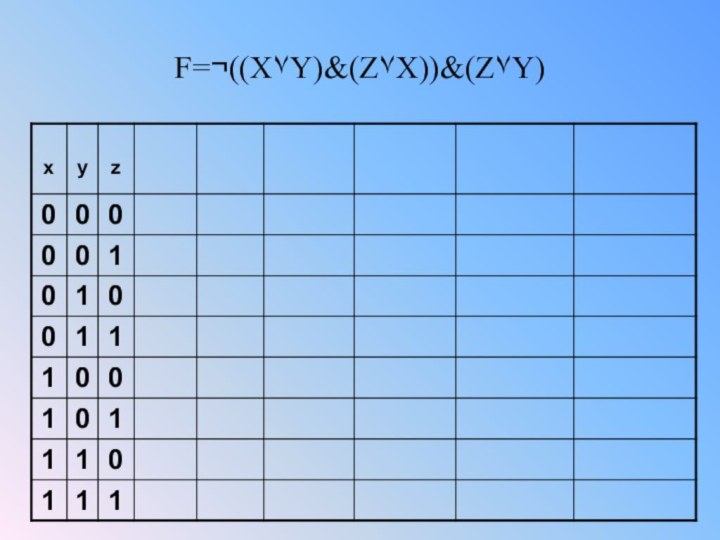
Построить таблицу истинности
F=¬((X۷Y)&(Z۷X))&(Z۷Y)
Слайд 5
Существует три способа решения логических задач:
1)Средствами алгебры
логики.
2)Табличный способ.
3)С помощью рассуждений.
Слайд 6
Схема решения логических задач:
Изучается
условие задачи.
Вводится система обозначений.
Составляется логическая формула.
Определяется значения логической формулы.
Слайд 7
Задача «История Нового года»
Три друга обсуждали историю Нового
года, при этом каждый сказал следующее:
Празднование Нового года с
1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем)
Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX
Празднование Нового года с 1 января установили во 2 веке и не французы
Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений.
Где и в какое время было установлено празднование Нового года с 1 января?
Слайд 8
Задача «История Нового года»
Три друга обсуждали историю Нового года, при этом каждый сказал следующее:
Празднование Нового года с 1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем)
Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX
Празднование Нового года с 1 января установили во 2 веке и не французы
Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений.
Где и в какое время было установлено празднование Нового года с 1 января?
Слайд 9
Задача «История Нового года»
Обозначения:
Ф – французы
Р –
римляне
К – Карл IX в 1659
Ц – Цезарь
В
–2 век
Слайд 10
Логическая формула:
(Ф&неЦ + неФ&Ц)&(Р&неК + неР&К)&
&(неВ&неФ +Ф&В)=
упростим логическую формулу
воспользуемся распределительным законом
Слайд 11
Логическая формула:
(Ф&неЦ + неФ&Ц)&(Р&неК + неР&К)&
&(неВ&неФ
+Ф&В)=
=((Ф&неЦ+неФ&Ц)&Р&неК+(Ф&неЦ+неФ&Ц)&
&неР&К)&(неВ&неФ+Ф&В)=
=(Ф&неЦ&Р&неК+неФ&Ц& Р&неК+Ф&неЦ& &неР&К+неФ&Ц&неР&К)&(неВ&неФ+Ф&В)=
Т.к. Ф&Р=0, Ц&К=0, то получаем
следующую формулу
Слайд 12
Логическая формула:
=(неФ&Ц& Р&неК+Ф&неЦ&неР&К)&
&(неВ&неФ+Ф&В)=
= (неФ&Ц& Р&неК+Ф&неЦ& неР&К)&неВ&неФ+ (неФ&Ц& Р&неК+Ф&неЦ&
неР&К)&Ф&В=
Т.к. Ф&неФ=0, неФ&неФ=неФ, Ф&Ф=Ф
то получаем
=неФ&Ц&Р&неК&неВ+Ф&неЦ&неР&К&В=
Логическая формула:
=(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&
&(неВ&неФ+Ф&В)=
= (неФ&Ц& Р&неК+Ф&неЦ& неР&К)&неВ&неФ+
(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&Ф&В=
Т.к. Ф&неФ=0, неФ&неФ=неФ, Ф&Ф=Ф
то получаем
=неФ&Ц&Р&неК&неВ+Ф&неЦ&неР&К&В,
т.к. К&В=0, то получаем следующую формулу:
Слайд 14
Логическая формула:
=Ц&Р&неК&неВ&неФ
формула принимает значение
истинно только при Ц=1, Р=1, К=0, В=0, Ф=0
Ответ:
Празднование
Нового года с 1 января установили римляне в 45 году до Рождества Христова
(благодаря введению нового календаря Юлием Цезарем )
Слайд 15
ЗАДАЧА 1
В симфонический оркестр приняли на работу трёх
музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке,
флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Слайд 16
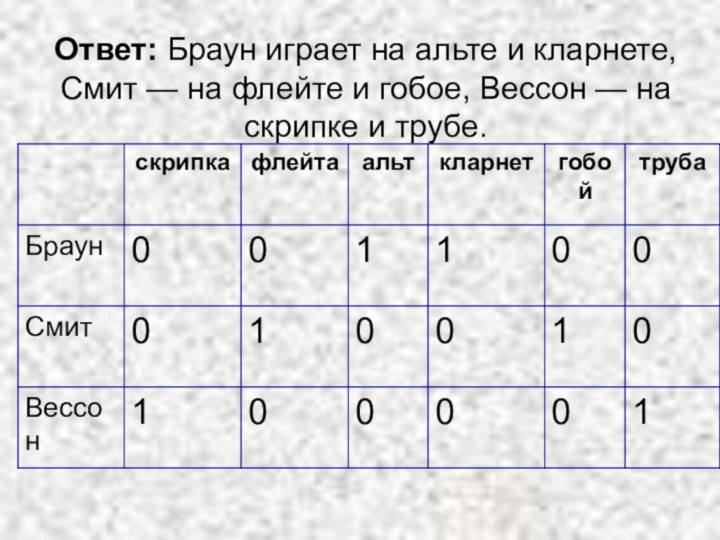
Ответ: Браун играет на альте и кларнете, Смит
— на флейте и гобое, Вессон — на скрипке
и трубе.
Слайд 17
ЗАДАЧА 2
Три одноклассника — Влад, Тимур и Юра,
встретились спустя 10 лет после окончания школы. Выяснилось, что
один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Слайд 18
Ответ. Влад — юрист и регбист, Тимур —
врач и турист, Юра — физик и бегун
Слайд 19
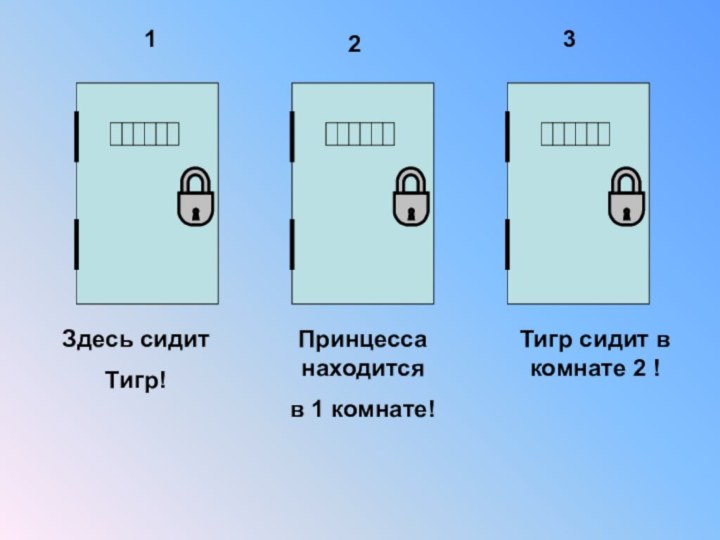
Здесь сидит
Тигр!
Принцесса находится
в 1 комнате!
Тигр сидит в комнате
2 !
1
2
3
Слайд 21
Решить логическую задачу
Синоптик объявляет прогноз
погоды на завтра и утверждает следующее:
Если не будет ветра,
то будет пасмурная погода без дождя.
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?
Слайд 22
Решение
Выделим простые высказывания и запишем их через переменные:
A – «Ветра нет»
B
– «Пасмурно»
С – «Дождь»
Слайд 23
2. Запишем логические функции
(сложные высказывания)
а) Если не
будет ветра, то будет пасмурная погода без дождя
__
A → B & C
б) Если будет дождь, то будет пасмурно и без ветра
С → B & A
в) Если будет пасмурная погода, то будет дождь и не будет
ветра
B → C & A
Слайд 24
3.Запишем произведение указанных функций:
_
F=(A→ B &
C) & (C→B & A) & (B→ C & A)
Слайд 25
4. Упростим формулу:
_
F=(A→ B & C) &
(C→B & A) & (B→ C & A) =
_ _ _ _
= (A v B & C) & (C v B&A) & (B v C&A) =
_ _ _ _
= (A v B & C) & (B v C&A) & (C v B&A) =
Слайд 26
4. Упростим формулу:
_
F=(A→ B & C) &
(C→B & A) & (B→ C & A) =
_ _ _ _
= (A v B & C) & (C v B&A) & (B v C&A) =
_ _ _ _
= (A v B & C) & (B v C&A) & (C v B&A) =
_ _ _ _ _ _ __
= (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)=
Слайд 27
4. Упростим формулу:
_
F=(A→ B & C) &
(C→B & A) & (B→ C & A) =
_ _ _ _
= (A v B & C) & (C v B&A) & (B v C&A) =
_ _ _ _
= (A v B & C) & (B v C&A) & (C v B&A) =
_ _ _ _ _ _ __
= (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)=
_ _ _ _ _ _ _ _ _ _
= A & B &(C v B&A) =A&B&C v A&B&B&A =
_ _ _
= A&B&C
Слайд 28
5. Приравняем результат к единице:
_ _ _
F = A & B & C = 1
Слайд 29
6. Проанализируем результат:
Логическое произведение равно 1, если каждый
множитель равен 1.
Поэтому:
_ _ _
A = 1; B = 1; C = 1;
Значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Слайд 30
Для чего мы изучаем алгебру логики?
Есть ли связь
между алгеброй логики и компьютерной техникой?
Слайд 31
Решить логическую задачу
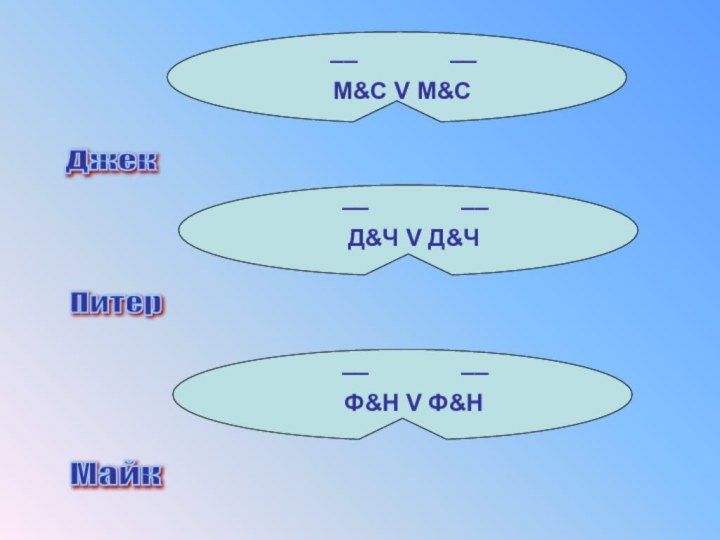
Джеку, Питеру и Майку предъявлено обвинение
в соучастии в ограблении банка. Похитители скрылись на поджидавшем
их автомобиле. На следствии Джек показал, что преступники скрылись на синем Мерседесе, Питер сказал, что это был черный Джип, а Майк утверждал, что это был Форд Мустанг и ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо марку машины, либо только ее цвет. Какого цвета и какой марки была машина?
Слайд 32
Выделим простые высказывания и запишем их через переменные:
М
– марка машины Мерседес;
С – цвет синий;
Д – марка
машины Джип;
Ч – цвет черный;
Ф – марка машины Форд Мустанг;
Н – цвет не синий.