Презентация на тему к уроку Перевод чисел из одной системы счисления в другую

количественный эквивалент («вес») цифры зависит то ее местоположения в

записи числа.

Основные достоинства любой позиционной системы счисления:
1. Простота выполнения арифметических операций.
2. Ограниченное количество символов, необходимых для записи числа.

число может быть представлено в виде:
Аq = ± (an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+a-2q-2+…a-mq-m)

- развернутая форма записи числа.
Здесь:
А - само число,
q — основание системы счисления,
аi — цифры данной системы счисления (an-2; an-1 и др.),
n — число разрядов целой части числа,
m — число разрядов дробной части числа.

Например: записать в развернутом виде числа

из любой системы счисления в десятичную:
Представьте число в развернутой

форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
Найдите сумму ряда. Полученное число является значением числа в десятичной системе счисления.

Пример 1
Переведем число 11012 в десятичную систему счисления.
1)Запишем число в развернутой форме: 11012= 1*23+1*22+1*21 + 1*20
2)Найдем сумму ряда: 8+4+2+1 = 1310

Пример 2
Переведем число 0,1235
1)Запишем число в развернутой форме: 0,1235 = 1*5-1+2*5-2+3*5-3
2) Найдем сумму ряда: 0,2+0,08+0,024 = 0,30410

чисел из десятичной системы счисления в любую другую:
Последовательно выполнять

деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
Составить число в новой системе счисления, записывая его, начиная с последнего частного.

37

2

18

2

1

9

2

4

2

2

2

1

0

1

0

0

Пример 1. перевести число 37 в двоичную систему

Получаем 3710=1001012

Пример 2. перевести число 126 в восьмеричную систему

126

8

15

8

1

6

7

Получаем 12610=1768

из десятичной системы в любую другую:
Последовательно умножаем данное число

и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или будет достигнута требуемая точность представления числа.
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

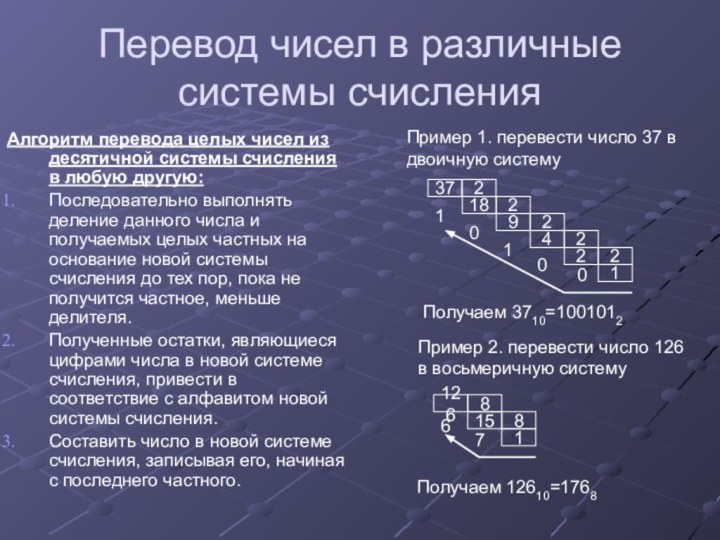
Пример 1. перевести число 0,6562510 в восьмеричную систему

Получаем: 0,6562510=0,528

Пример 2. перевести число 0,6562510 в шестнадцатеричную систему

Получаем: 0,6562510=0,А816