- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Содержательный подход к измерению информации (10 класс)
Содержание
- 2. СодержаниеКоличество информации как мера уменьшения неопределенности знанийОпределение количества информации
- 3. Информативность сообщенияЕсли сведения «старые», то есть человек
- 4. ПримерыВопрос: - Какой город является столицей Франции?Ответ:-
- 5. ПримерыВопрос:- Что изучает коллоидная химия?Ответ:- Коллоидная химия
- 6. ПримерыВопрос:- Какую высоту и вес имеет Эйфелева
- 7. Информативность сообщенияЕсли сообщение неинформативно для человека, то
- 8. Информация и неопределенностьПример: вы услышали по телевизору,
- 9. После написания контрольной работы мы думаем какую
- 10. Бросание монетУ монеты, как известно, две стороны:«герб»
- 11. Бросание кубикаИгральный кубик — это кубик, грани
- 12. Неопределенность знанийНеопределенность знания о результате некоторого события
- 13. Равновероятные событияСобытия равновероятны, если ни одно из
- 14. Определение количества информации
- 15. Как же измерить количество информации?Да также, как
- 16. 1 бит информацииКоличество информации можно рассматривать как
- 17. Определение информацииЕсли «Ваньку-Встаньку» качнуть, то сколько различных
- 18. Определение информацииБудем бросать монету.Сколько вариантов выпадения может
- 19. Определение информацииБудем бросать 2 монеты.Бросание 2 монет
- 20. Определение информацииБудем бросать 3 монеты.При бросание 3
- 21. Отгадывание чиселДопустим кто-то загадал число от 1
- 22. Сценарий отгадывания числаПусть загадано число 5 (мы
- 23. Определение информацииА если мы будем бросать 6-гранный
- 24. Определение информацииСоставим таблицу из предыдущих примеров:
- 25. Определение информацииЕсли посмотреть таблицу, то можно заметить
- 26. Определение информацииЕсли N = 2 (2=21),то уравнение
- 27. Определение информацииНапример, желая определить, сколько же бит
- 28. Задания для закрепленияПример 1.Сколько информации несет сообщение
- 29. Задания для закрепленияПример 2.Сколько информации несет сообщение
- 30. Задания для закрепленияПример 3.Проводятся две лотереи «4
- 31. Решение:Вытаскивание любого номера из лотерейного барабана –
- 32. Задания для закрепленияПример 4.В течение четверти ученик
- 33. Решение: Данный результат мог быть получен путем
- 34. Единицы измерения количества информации
- 35. Самостоятельное решениеЗадача 1.Вы подошли к светофору, когда
- 36. Самостоятельное решениеЗадача 2.Сообщение о том, что ваш
- 37. Самостоятельное решениеЗадача 3.В корзине 8 шаров.Все шары
- 38. Самостоятельное решениеЗадача 4.Сколько бит информации несет сообщение
- 39. Самостоятельное решениеЗадача 5.в школьной библиотеке 16 стеллажей
- 40. Самостоятельное решениеЗадача 6.При угадывании целого числа в
- 41. Самостоятельное решениеЗадача 7.Сообщение о том, что Петя
- 42. Разновероятностный подходВ 1948 г. американский инженер и
- 43. Задания для закрепленияЗадача:В коробке имеется 40 белых
- 44. Самостоятельное решениеВ пруду живут 8000 карасей, 2000
- 45. Используемая литератураИ. Семакин. Информатика. Базовый курс. 7
- 46. Скачать презентацию
- 47. Похожие презентации
СодержаниеКоличество информации как мера уменьшения неопределенности знанийОпределение количества информации











































Слайд 2
Содержание
Количество информации как мера уменьшения неопределенности знаний
Определение количества
информации
Слайд 3
Информативность сообщения
Если сведения «старые», то есть человек это
уже знает, или содержание сообщения непонятно человеку, то для
него это сообщение неинформативно.Информативно то сообщение, которое содержит новые и понятные сведения.
Слайд 4
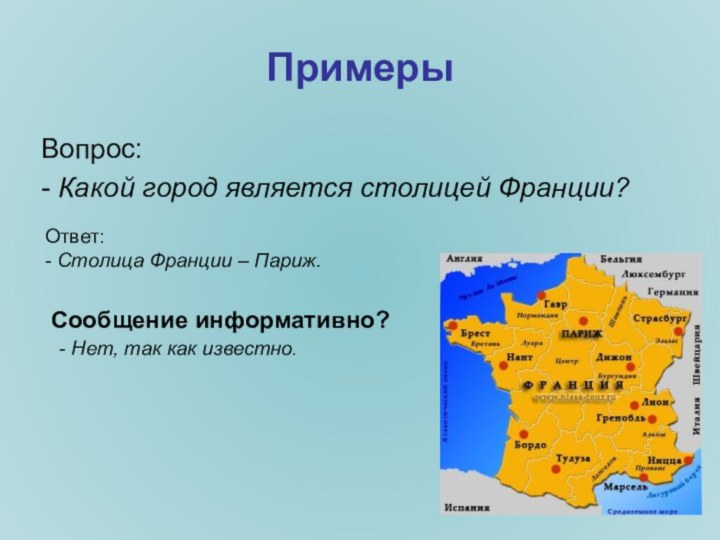
Примеры
Вопрос:
- Какой город является столицей Франции?
Ответ:
- Столица
Франции – Париж.
Сообщение информативно?
- Нет, так как известно.
Слайд 5
Примеры
Вопрос:
- Что изучает коллоидная химия?
Ответ:
- Коллоидная химия изучает
дисперсионные состояния систем, обладающих высокой степенью раздробленности.
Сообщение информативно?
- Нет,
так не понятно.
Слайд 6
Примеры
Вопрос:
- Какую высоту и вес имеет Эйфелева башня?
Ответ:
- Эйфелева башня имеет
высоту 300 метров
и вес 9000 тонн.
Сообщение
информативно?- Да.
Слайд 7
Информативность сообщения
Если сообщение неинформативно для человека, то количество
информации в нем с точки зрения этого человека равно
нулю.Количество информации в информативном сообщении больше нуля.
Слайд 8
Информация и неопределенность
Пример: вы услышали по телевизору, что
завтра будет солнечная погода.
Ваше состояние изменилось: вы стали обладателем
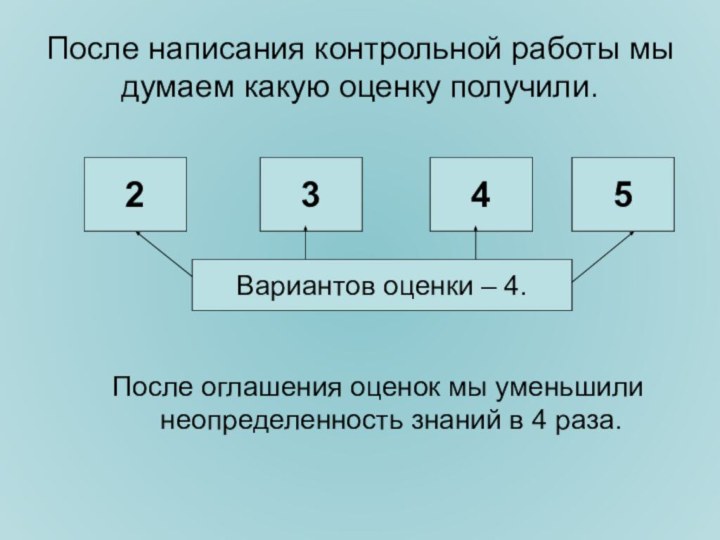
информации, а неопределенность, которая до этого существовала, исчезла.Слайд 9 После написания контрольной работы мы думаем какую оценку
получили.
После оглашения оценок мы уменьшили неопределенность знаний в 4
раза.
Слайд 10
Бросание монет
У монеты, как известно, две стороны:
«герб» «решка»
Если бросить ее на стол, монета обязательно упадет вверх
либо «гербом», либо «решкой».Таким образом, монету, лежащую на столе, можно рассматривать как простейшую систему, которая может находиться в одном из двух возможных состояний.
Слайд 11
Бросание кубика
Игральный кубик — это кубик, грани которого
пронумерованы от 1 до 6.
Аналогично монете игральный кубик, лежащий
на столе, — это система, находящаяся в одном из шести возможных состояний (по номерам граней, обращенных вверх).
Слайд 12
Неопределенность знаний
Неопределенность знания о результате некоторого события –
это число возможных вариантов результата.
Для монеты – 2, для
кубика – 6, для билетов – 30 (если на столе лежало 30 билетов).Чем больше равновозможных событий, тем больше неопределенность ситуации.
Слайд 13
Равновероятные события
События равновероятны, если ни одно из них
не имеет преимущества перед другими.
С этой точки зрения выпадение
«герба» или «решки» – равновероятно.
Слайд 15
Как же измерить количество информации?
Да также, как мы
измеряем длину или массу чего-нибудь: сравнить с соответствующим эталоном.
Надо
только выбрать эталон.Например, в мультфильме
«38 попугаев» эталоном длины
служит длина шага попугая.
Каков же эталон для измерения информации?
Давайте в этом разберемся.
Слайд 16
1 бит информации
Количество информации можно рассматривать как меру
уменьшения неопределенности знания при получении информационных сообщений.
Сообщение, уменьшающее
неопределенность знаний в 2 раза, несет 1 бит информации. Сообщение о том, что произошло одно событие из двух равновероятных, несет 1 бит информации.
Бит - binary digit (двоичный знак).
Слайд 17
Определение информации
Если «Ваньку-Встаньку» качнуть, то сколько различных вариантов
его конечного состояния получим?
- Один вариант («Ванька-Встанька» всегда встает).
То
есть вероятность события равна 1 (100% выполнение).И мы не получаем ни чего нового и неизвестного при этом, то есть информация равна 0.
Слайд 18
Определение информации
Будем бросать монету.
Сколько вариантов выпадения может быть?
– 2
Вероятность выпадения «герба» или «решки» - ½.
Количество информации
– 1 бит.
Слайд 19
Определение информации
Будем бросать 2 монеты.
Бросание 2 монет должно
принести 2 бита информации, так как количество монет увеличилось
в 2 раза.Количество различных вариантов выпадения по две монеты: 4.
Вероятность появления 1 варианта – ¼
Слайд 20
Определение информации
Будем бросать 3 монеты.
При бросание 3 монет
количество информации увеличится в 3 раза по сравнению с
бросанием 1 монеты.Количество различных вариантов выпадения по 3 монеты: 8
Вероятность выпадения 1 варианта: 1/8.
Слайд 21
Отгадывание чисел
Допустим кто-то загадал число от 1 до
16.
Сколько чисел можно загадать? - 16.
Вероятность загадать любого числа
из этого промежутка: 1/16.Отгадывание происходит по такому сценарию:
Задается такой вопрос на который можно получить один из вариантов ответа: «да» или «нет».
Слайд 22
Сценарий отгадывания числа
Пусть загадано число 5 (мы не
знаем это).
1 вопрос (даст 1 бит информации):
- Больше 8?
– Нет.2 вопрос (даст 2 бит информации):
- Больше 4? – Да.
3 вопрос (даст 3 бит информации):
-Больше 6? – Нет.
4 вопрос (даст 4 бит информации):
-Больше 5? – Нет.
Ответ: Задуманное число 5.
Вывод:
При отгадывании задуманного числа в диапазоне от 1 до 16, достаточно 4 вопроса (получение 4 бита информации).
Слайд 23
Определение информации
А если мы будем бросать 6-гранный кубик?
Количество
вариантов выпадения одной из 6 сторон: 6.
Вероятность выпадения одной
из 6 сторон: 1/6.Сколько же будет получено
информации при выпадении
одной из 6 сторон?
Слайд 25
Определение информации
Если посмотреть таблицу, то можно заметить закономерность.
От
частных примеров приходим к обобщенной формуле:
Если ввести обозначения:
N –
число вариантов равновероятных событий (неопределенность знаний),i – количество информации в сообщении о том, что произошло одно из N событий.
N = 2i
Слайд 26
Определение информации
Если N = 2 (2=21),
то уравнение примет
вид 2i = 21,
отсюда i = 1.
Если N =
4 (4=22),то уравнение примет вид 2i = 22,
отсюда i = 2.
Если N = 8 (8=23),
то уравнение примет вид 2i = 23,
отсюда i = 3.
В общем случае, если N = 2k,
где k- целое число,
то уравнение примет вид 2i = 2k,
отсюда i = k.
Слайд 27
Определение информации
Например, желая определить, сколько же бит информации
несет сообщение о результате бросания шестигранного кубика, нужно решить
уравнение2i = 6.
Поскольку 22 < 6 < 23, то получаем 2 < i < 3.
Используя инженерный калькулятор, узнаем, что i=2,58496.
Слайд 28
Задания для закрепления
Пример 1.
Сколько информации несет сообщение о
том, что из колоды карт достали карту красной масти?
Решение:
1
бит, т. к. N = 2 (красных и черных карт одинаковое количество).2i = 2
Слайд 29
Задания для закрепления
Пример 2.
Сколько информации несет сообщение о
том, что из колоды карт достали карту бубновой масти?
Решение:
2
бита, так как т. к. N = 4 (всего в колоде 4 масти, и количество карт в них одинаковое).2i = 4
Слайд 30
Задания для закрепления
Пример 3.
Проводятся две лотереи «4 из
32» и «5 из 64».
Сообщение о результатах, какой из
лотерейнесет больше информации?
Слайд 31
Решение:
Вытаскивание любого номера из лотерейного барабана – события
равновероятные.
Поэтому в первой лотерее количество информации в сообщении об
одном номере равно 5 бит (25 = 32), а во втором – 6 бит (26 = 64).Сообщение о 4-х номерах в первой лотерее несет 5 * 4 = 20 бит.
Сообщение о 5-ти номерах второй лотереи несет 6 * 5 = 30 бит.
Следовательно, сообщение о результатах второй лотереи несет больше информации, чем первой.
Слайд 32
Задания для закрепления
Пример 4.
В течение четверти ученик получил
100 оценок.
Сообщение о том, что он получил четверку, несет
2 бита информации.Сколько четверок ученик получил за четверть?
Слайд 33
Решение:
Данный результат мог быть получен путем следующих рассуждений:
2
бита информации несет сообщение об одном из четырех равновероятных
событий (22 = 4).То есть вероятность получения четверок равна ¼.
Тогда количество четверок определится как:
100 / 4 = 25.
Таким образом, в течение четверти ученик получил 25 четверок.
Слайд 34 Единицы измерения количества информации 1 байт = 8
битов = 23 битов
1 килобайт (Кбайт) = 210 байт
= 1024 байт1 мегабайт (Мбайт) = 210 Кбайт = 1024 Кбайт
1 гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт
1 терабайт (Тбайт) = 210 Гбайт = 1024 Гбайт
Слайд 35
Самостоятельное решение
Задача 1.
Вы подошли к светофору, когда горел
желтый свет.
После этого загорелся зеленый.
Какое количество информации вы при
этом получили?Ответ: 1бит
Слайд 36
Самостоятельное решение
Задача 2.
Сообщение о том, что ваш друг
живет на 9 этаже, несет 4 бита информации. Сколько
этажей в доме?Ответ: 16 (24 = 16).
Слайд 37
Самостоятельное решение
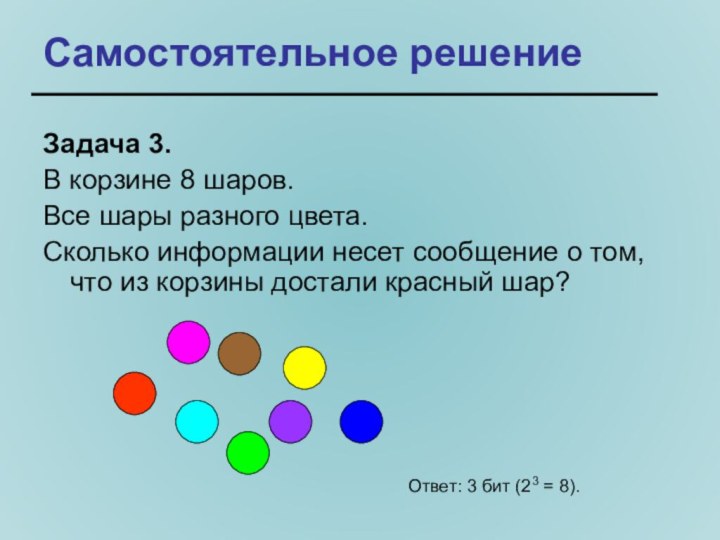
Задача 3.
В корзине 8 шаров.
Все шары разного
цвета.
Сколько информации несет сообщение о том, что из корзины
достали красный шар?Ответ: 3 бит (23 = 8).
Слайд 38
Самостоятельное решение
Задача 4.
Сколько бит информации несет сообщение о
том, что из колоды в 32 карты достали даму
крести?Ответ: 5 бит (2X = 32).
Слайд 39
Самостоятельное решение
Задача 5.
в школьной библиотеке 16 стеллажей с
книгами.
На каждом стеллаже 8 полок.
Библиотекарь сообщил Пете, что нужная
ему книга находится на пятом стеллаже на третьей сверху полке.Какое количество информации библиотекарь передал Пете?
Ответ: 7 бит
16*8 = 128 полок всего
2Х = 128
Слайд 40
Самостоятельное решение
Задача 6.
При угадывании целого числа в некотором
диапазоне было получено 6 бит информации.
Сколько чисел содержится в
этом диапазоне?Ответ: 64 (26 = 64).
Слайд 41
Самостоятельное решение
Задача 7.
Сообщение о том, что Петя живет
во втором подъезде, несет 3 бита информации.
Сколько подъездов в
доме?Ответ: 8 (23 = 8).
Слайд 42
Разновероятностный подход
В 1948 г. американский инженер и математик
К Шеннон предложил формулу для вычисления количества информации для
событий с различными вероятностями.Если i - количество информации, k - количество возможных событий, рi - вероятности отдельных событий, то количество информации для событий с различными вероятностями можно определить по формуле:
i = - ∑ рi log2 рi, где i принимает значения от 1 до k.
Слайд 43
Задания для закрепления
Задача:
В коробке имеется 40 белых и
10 черных шаров. Определите количество информации.
Решение:
Всего шаров: 40+10 =
50Вероятность вытащить белый шар:
рб =0,8
i = - ∑ рi log2 рi =-(рб * log2 рб + рч * log2 рч)
i =-(0,8 * log2 0,8 + 0,2 * log2 0,2) =….
Вероятность вытащить черный шар: рч =0,2
Слайд 44
Самостоятельное решение
В пруду живут 8000 карасей, 2000 щук
и 400000 пескарей.
Вероятнее наловить больше карасей, щук или пескарей.
Слайд 45
Используемая литература
И. Семакин. Информатика. Базовый курс. 7 –
9 классы. – М.: Лаборатория Базовых Знаний, 2001. –
364 с.: ил.Информатика. Задачник-практикум в 2 т./Под ред. И.Г. Семакина, Е.К. Хеннера: Том 1. – М.: Лаборатория Базовых Знаний, 2001. – 304 с.: ил.
Урок: Определение количества информации 8 класс: http://netedu.ru/node/3986
Решение задач на определение количества информации: http://uprobr.ucoz.ru/publ/informatika_i_ikt/reshenie_zadach_na_opredelenie_kolichestva_informacii/6-1-0-551
Карта Франции: http://tgekb.ru/pics500/userimages/article/frantsiya880090938francemap1.jpg
Коллоидная химия: http://www.char.ru/books/2066990_Kolloidnaya_himiya_Uchebnik_dlya_vuzov.jpg
Эйфелева башня: http://mosaica.ru/sites/default/files/news/preview/2010/02/27/888888888888888.jpg





























