- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Как научить ребенка решать задачи по информатике из раздела Логика
Содержание
- 2. Ло́гика (др.-греч. λογική — «наука о правильном
- 3. Логика - это фундаментальная основа информатики как
- 4. Решение логических зада на уроках информатики в
- 5. Далее изучение основ логики разбито на 2
- 6. Задачи:Научить учащихся формализовывать высказывания.Выделять существенные высказывания в
- 7. Решение логических задач с помощью рассуждений. Перед
- 8. Решение (метод рассуждений):1) Есть «точная» информация, которая не
- 9. Решение задач с помощью таблицОсновной прием, который
- 11. Решение. Составим таблицу и отразим в ней условия
- 12. Из условия 4 следует, что Смит не
- 13. Из условий 1 и 2 следует, что
- 14. Ответ: Браун играет на альте и кларнете, Смит
- 15. Решение логических задач графическим способомВ бутылке, стакане,
- 20. На схеме осталось только 4 связи,
- 21. В классе 30 учащихся. Из них 18
- 22. В таблице приведены запросы к поисковому серверу:
- 23. Решение:Воспользуемся кругами Эйлера (диаграммами Вена):Ответ: 4123.задания
- 27. Для какого числа X истинно высказывание:((x
- 28. Для какого имени ложно высказывание:(первая буква гласная
- 29. Построить таблицу истинности для следующей функции:F(X,Y,Z)=(x→y)^z +
- 34. Скачать презентацию
- 35. Похожие презентации
Ло́гика (др.-греч. λογική — «наука о правильном мышлении», «способность к рассуждению» от др.-греч. λόγος —«рассуждение», «мысль», «разум») — раздел философии, нормативная[1] наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка.






















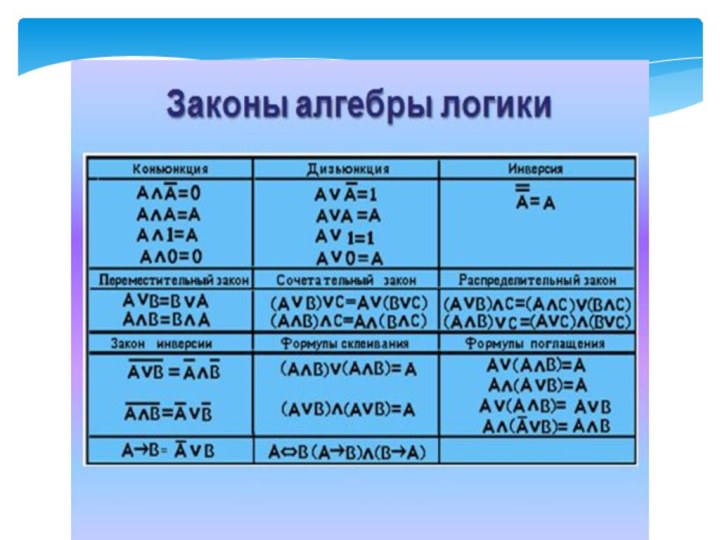






Слайд 3 Логика - это фундаментальная основа информатики как науки.
Элементы и основы математической логики заложены в логические элементы
и логические устройства ЭВМ, в основы алгоритмизации и языки программирования, в процедуры поиска информации в базах данных и в сети Интернет, а также в системах логического программирования, базах знаний и экспертных системах на ЭВМ.Логика в информатике используется в поиске информации в Интернет, в базах данных, в базах знаний, в алгоритмах, алгоритмизации и во всех языках программирования.
Слайд 4 Решение логических зада на уроках информатики в начальной
школе представляет собой один из приемов развития мышления.
Изучение
основ логики в 5-7 классах предполагает отработку навыков по решению логических задач, которые были заложены в курсе начальной школы.Слайд 5 Далее изучение основ логики разбито на 2 части:
«Элементы формальной логики» и «Элементы математической логики» изучаются в
8 классе, что позволяет выделить и закрепить знания о понятиях и суждениях, доказательных рассуждениях, о логических законах, сформировать умения оперировать символикой математической логики, применять эти умения к решению логических содержательных задач, а «Логические основы устройства ЭВМ» – в 9 классе, что позволяет сформировать знания об архитектуре и принципах функционирования ЭВМ.
Слайд 6
Задачи:
Научить учащихся формализовывать высказывания.
Выделять существенные высказывания в тексте
задачи.
Научить учащихся предоставлять условия и решения задачи в формализованном
виде.Преобразовывать логические выражения в соответствии с законами и свойствами.
Строить логическую схему устройства с заданными характеристиками.
Находить ошибки в рассуждениях.
При изучении данной темы вводятся основные понятий математической логики, необходимых при изучении базового курса информатики, а также их использования при работе с прикладным программным обеспечением и в языках программирования.
Слайд 7
Решение логических задач с помощью рассуждений.
Перед началом
Турнира «Четырех» болельщики высказали следующие предположения по поводу своих
кумиров:А) Макс победит, Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс?
Слайд 8
Решение (метод рассуждений):
1) Есть «точная» информация, которая не подвергается
сомнению: каждый из болельщиков оказался прав в одном прогнозе.
2) Запишем
высказывания болельщиков:1. Макс победит, Билл – второй; 2. Билл – третий, Ник – первый; 3. Макс – последний, а первый – Джон.
3) Известно, что каждый из болельщиков только в одном из прогнозов был прав (то есть, из двух высказываний одно истинно, а другое – ложно).
4) Пусть первый болельщик угадал, что Макс победит, тогда третий болельщик ошибся в двух предположениях, а это не соответствует «точной» информации.
5) Пусть первый болельщик угадал, что Билл занял второе место, тогда второй болельщик предсказал первое место Нику, следовательно, по предположению третьего, Макс занял последнее место, а Джон – оставшееся третье место.
Отсюда имеем: Ник – первое, Билл – второе, Джон – третье и Макс – четвертое место.
.
Слайд 9
Решение задач с помощью таблиц
Основной прием, который используется
при решении текстовых логических задач, заключается в построении таблиц.
Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачиСлайд 11 Решение. Составим таблицу и отразим в ней условия задачи,
заполнив соответствующие клетки цифрами 0 и 1 в зависимости
от того, ложно или истинно соответствующее высказывание.Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Слайд 12 Из условия 4 следует, что Смит не играет
ни на альте, ни на трубе, а из условий
3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями:Из таблицы видно, что на трубе может играть только Вессон.
Слайд 13 Из условий 1 и 2 следует, что Смит
не скрипач. Так как на скрипке не играет ни
Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки "Вессон" можно заполнить нулями:Из таблицы видно, что играть на флейте и на гобое может только Смит.
Слайд 14 Ответ: Браун играет на альте и кларнете, Смит —
на флейте и гобое, Вессон — на скрипке и
трубе.
Слайд 15
Решение логических задач графическим способом
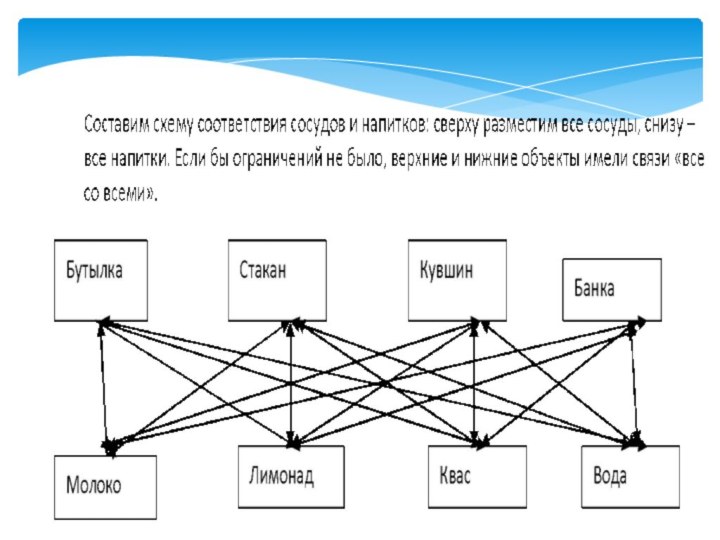
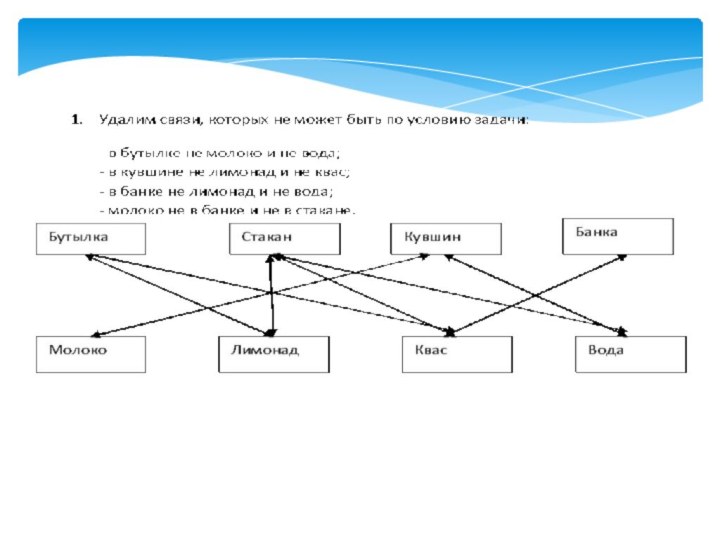
В бутылке, стакане, кувшине
и банке находятся молоко, лимонад, квас и вода. Известно,
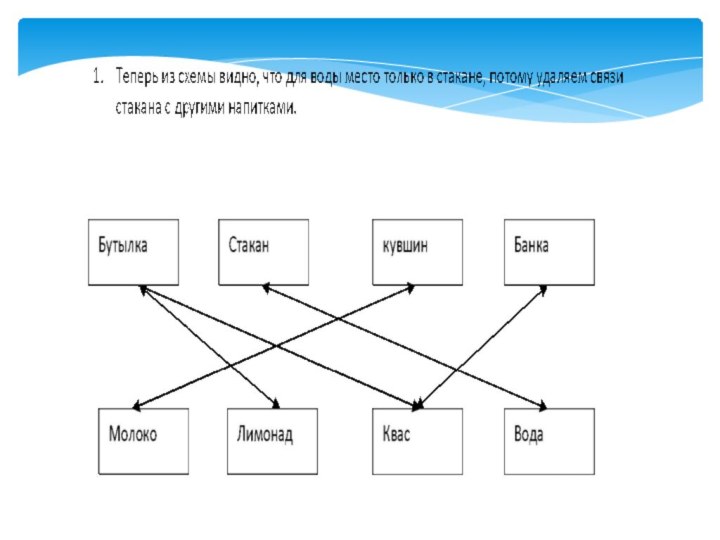
что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В каком сосуде находится квас?Слайд 20 На схеме осталось только 4 связи, и
можно ответить на поставленный вопрос: квас находится в банке.
Ответ: БанкаСлайд 21 В классе 30 учащихся. Из них 18 человек
занимаются в секции легкой атлетики, 10 – плаванием, 3
– и тем, и другим. Сколько человек не занимается ничем?30 - (7 + 3 + 15) = 5
Решение логическихзадач с помощью кругов Эйлера
Слайд 22
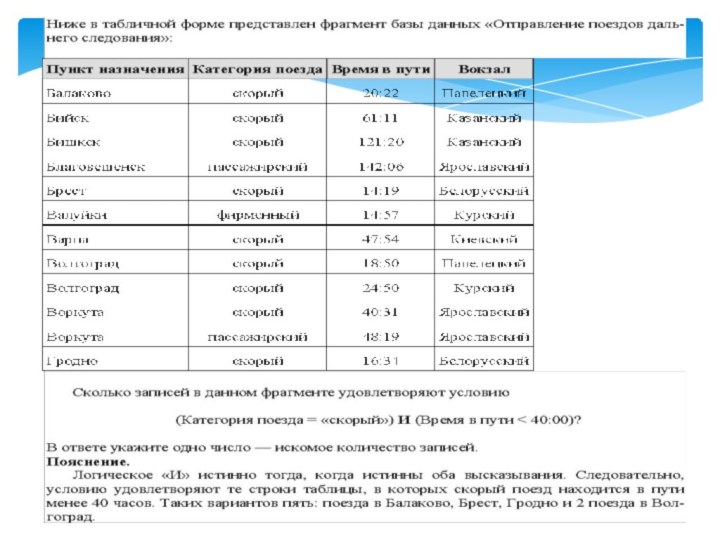
В таблице приведены запросы к поисковому серверу:
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» − &.
Слайд 27
Для какого числа X истинно высказывание:
((x
3)3 4)4
Решение:
Подставляем в выражение предложенные варианты ответа и определяем,
истинно выражение или ложно:1) x=1: ((1<4)→(1<3))^((1<3)→(1<1))=(1→1)^(1→0)
Сначала вычислим выражение в скобках:
(1→1)^(1→0)=1^0=0 (не подходит)
Аналогично подставляем другие варианты ответа, вычисляем:
2) x=2: ((2<4)→(2<3))^((2<3)→(2<1))=(1→1)^(1→0)=1^0=0 (не подходит)
3) x=3: ((3<4)→(3<3))^((3<3)→(3<1))=(1→0)^(0→0)=0^1=0 (не подходит)
4) x=4: ((4<4)→(4<3))^((4<3)→(4<1))=(0→0)^(0→0)=1^1=1 (подходит)
Ответ: 4.
Слайд 28
Для какого имени ложно высказывание:
(первая буква гласная ^последняя
буква согласная)→ ¬(третья буква согласная)?
Дмитрий 2) Антон 3) Екатерина
4) АнатолийРешение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:
Дмитрий: (0 ^ 1)→ ¬(0)=0→1 = 1 (не подходит)
Антон: (1 ^ 1)→ ¬(1)=1→0 = 0 (подходит)
Екатерина: (1 ^ 0)→ ¬(0)=0→1 = 1 ( не подходит)
Анатолий: (1 ^ 1)→ ¬(0)=1→1 = 1 ( не подходит)
Ответ: 2.
Слайд 29
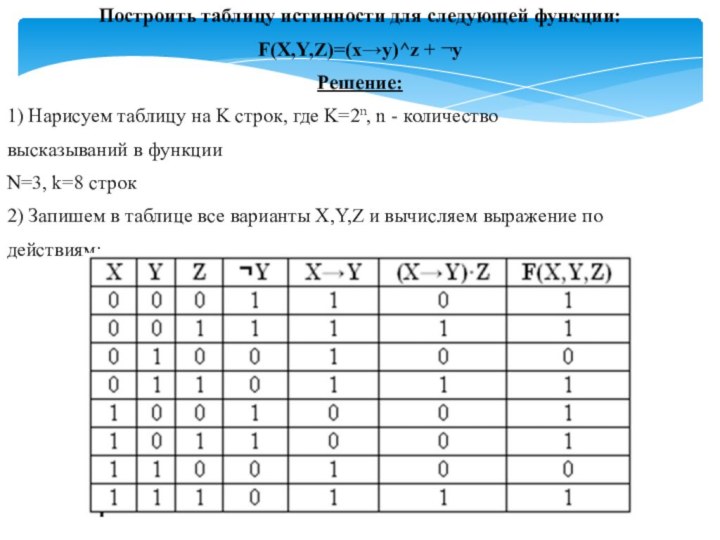
Построить таблицу истинности для следующей функции:
F(X,Y,Z)=(x→y)^z + ¬y
Решение:
1)
Нарисуем таблицу на K строк, где K=2n, n -
количествовысказываний в функции
N=3, k=8 строк
2) Запишем в таблице все варианты X,Y,Z и вычисляем выражение по
действиям: