двумя скрещивающими прямыми.
-нахождение расстояния от точки до плоскости.
Алгоритм
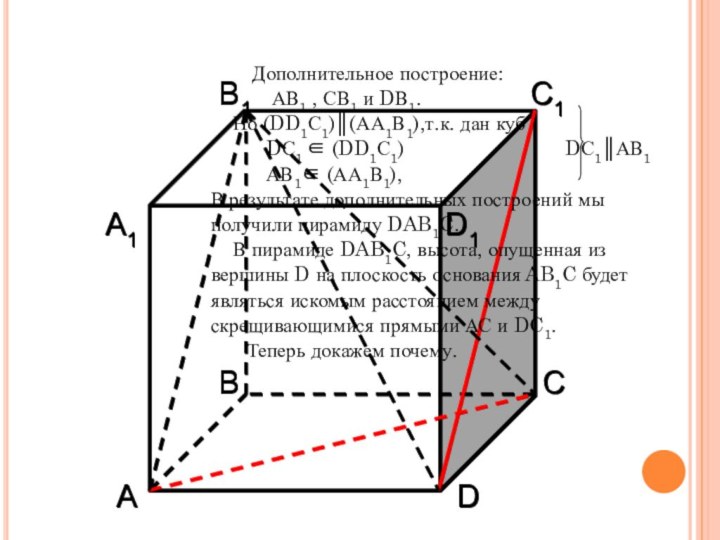
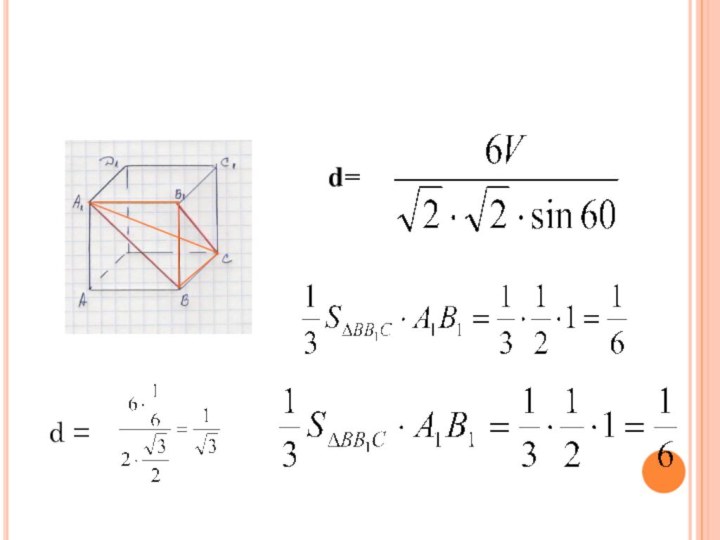
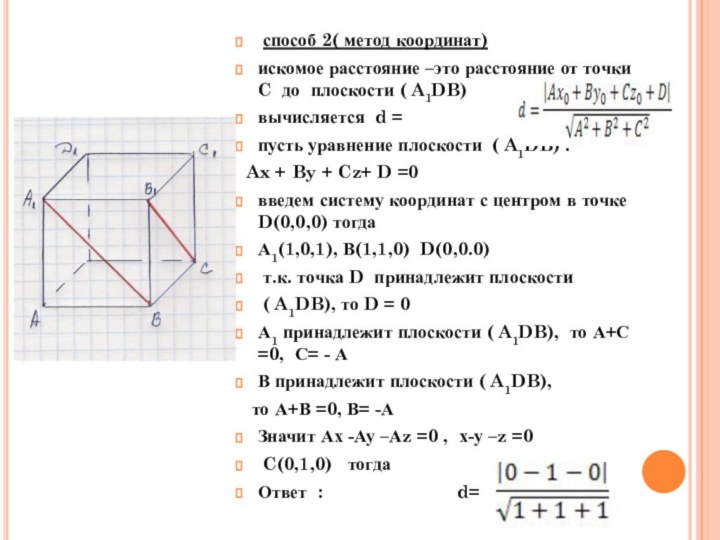
метода объемов. построить пирамиду, в которой высота, опущенная из вершины этой пирамиды на плоскость основания, является искомым расстоянием между двумя скрещивающимися прямыми;
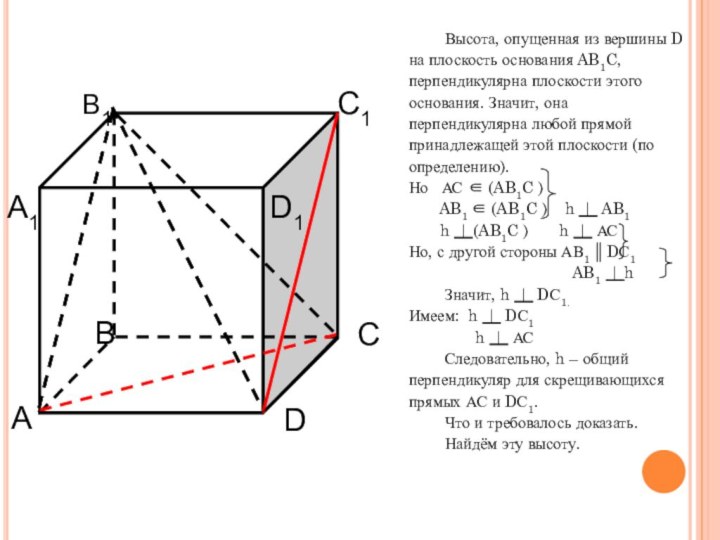
доказать, что эта высота и есть искомое расстояние;
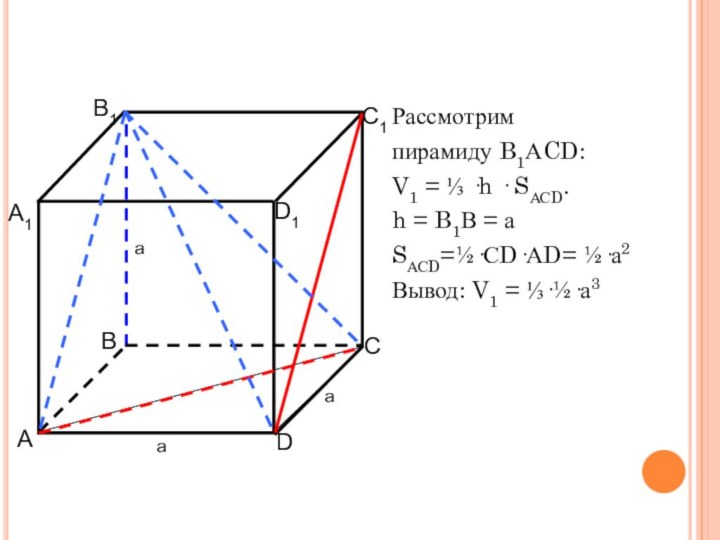
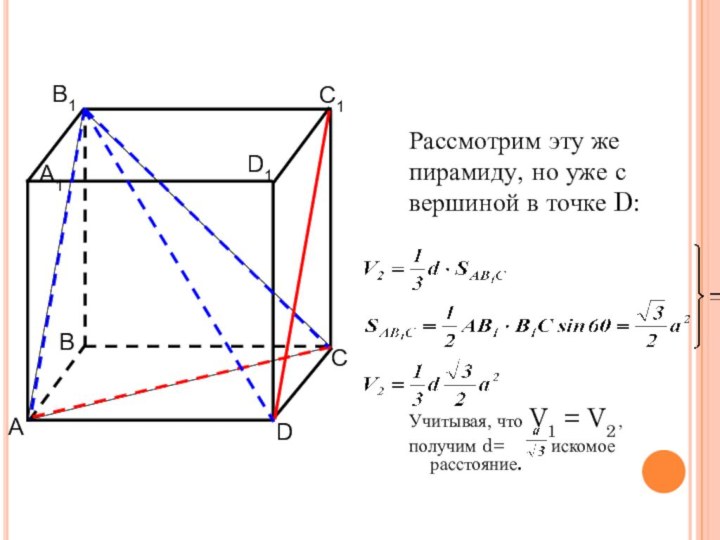
найти объём этой пирамиды двумя способами;
и выразить эту высоту;