Слайд 2
ЛОГИЧЕСКАЯ СХЕМА
Логическая схема – некоторое устройство (имеет вид
«черного ящика»), реализующее функции математической логики, в котором вход
– набор булевых переменных, а выход – булева функция.
x1
x2
xn
f(x1,x2,…,xn)
Логические схемы состоят из логических элементов, осуществляющих логические операции.
Слайд 3
Логические элементы подразделяются и по типу использованных в
них электронных элементов. Наибольшее применение в настоящее время находят
следующие логические элементы:
РТЛ (резисторно-транзисторная логика)
ДТЛ (диодно-транзисторная логика)
ТТЛ (транзисторно-транзисторная логика)
Упрощённая схема двухвходового элемента И-НЕ ТТЛ
Схема простейшего логического инвертора
Слайд 4
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Логический элемент– это устройство, реализующее ту или
иную логическую функцию.
При этом логические сигналы 0 и
1 задаются разными уровнями напряжения. Сигнал логического нуля обычно представляется низким уровнем напряжения, логической единицы – высоким.
Для изображения логических схем используются условные графические обозначения элементов, описывающие выполняемую элементами функцию.
Слайд 5
Стандарты условных обозначений
В настоящее время в мире существует
несколько общепринятых стандартов условных обозначений. Наиболее распространенными являются американский
стандарт milspec 806В и стандарт МЭК 117-15 А, созданный Международной Электротехнической Комиссией. Часто в литературе используются также обозначения в европейской системе DIN 4070. В отечественной литературе условные обозначения элементов в основном соответствуют ГОСТ 2.743-82.
Слайд 6
Основные логические элементы
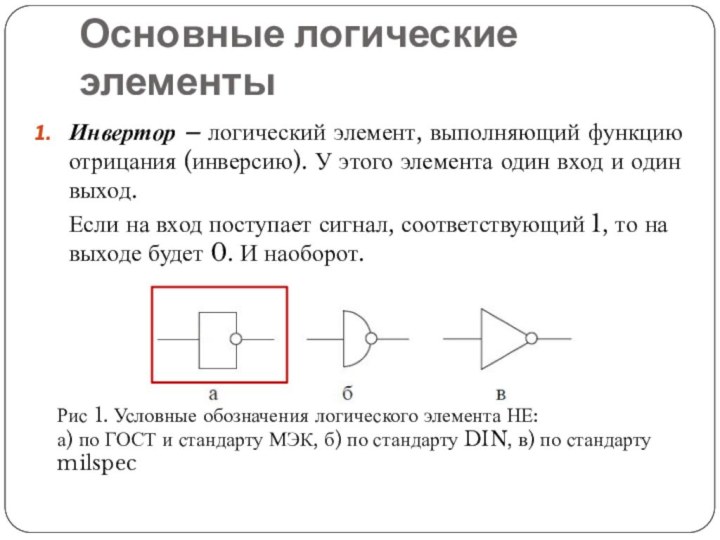
Инвертор – логический элемент, выполняющий функцию
отрицания (инверсию). У этого элемента один вход и один
выход.
Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
Рис 1. Условные обозначения логического элемента НЕ:
а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec
Слайд 7
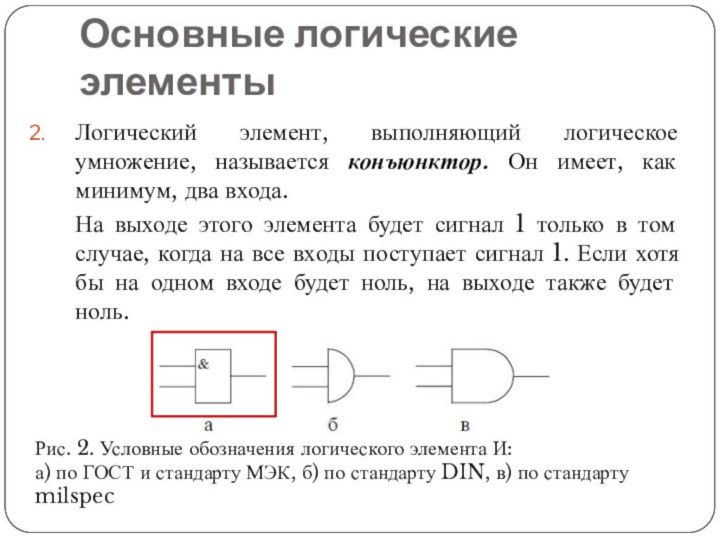
Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он
имеет, как минимум, два входа.
На выходе этого элемента будет
сигнал 1 только в том случае, когда на все входы поступает сигнал 1. Если хотя бы на одном входе будет ноль, на выходе также будет ноль.
Основные логические элементы
Рис. 2. Условные обозначения логического элемента И:
а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec
Слайд 8
Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он
имеет, как минимум, два входа.
Если хотя бы на один
вход поступает сигнал 1, то на выходе будет сигнал 1.
Основные логические элементы
Рис. 3. Условные обозначения логического элемента ИЛИ:
а) по ГОСТ, б) по стандарту МЭК, в) по стандарту DIN, г) по стандарту milspec
Слайд 9
Комбинационная схема – это логическая схема, в которой
значения выходных переменных в данный момент времени полностью определяются
значениями входных переменных.
Логическая схема с памятью - это логическая схема значения выходных сигналов которой зависят как от входных сигналов в данный момент времени, так и от сигналов, поступивших ранее.
Логические схемы
Логические схемы с памятью
Комбинационные схемы
Слайд 10
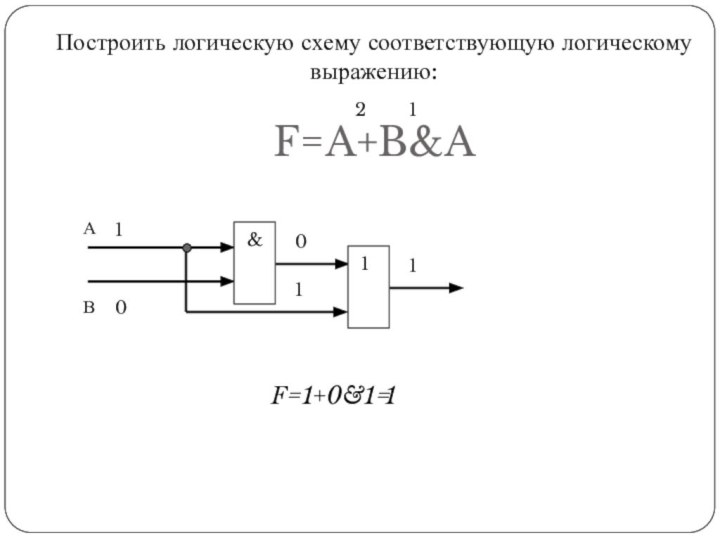
Построить логическую схему соответствующую логическому выражению:
Слайд 11
Этапы построения функциональной схемы устройства.
Построение таблицы истинности по
заданным условиям работы проектируемого узла (т.е. по соответствию его
входных и выходных сигналов).
Конструирование логической функции данного узла по таблице истинности, ее преобразование (упрощение), если это возможно и необходимо.
Составление функциональной схемы проектируемого узла по формуле логической функции.
Проверка правильности работы схемы.
Слайд 12
Построить логическую схему соответствующую логическому выражению:
f=a&b+(b+a)
1
2
3
4
Слайд 13
Построить логическую схему соответствующую логическому выражению:
f=a&b+(b+a)
1
2
3
4
а
в
1
0
0
1
0
1
0
0
0
Слайд 14
f=a v b & c, если а=1, в=1,
с=1.
Задание 1.
Постройте логические схемы, соответствующие логическим выражениям и выполните
проверку:
&
с
а
b
Слайд 16
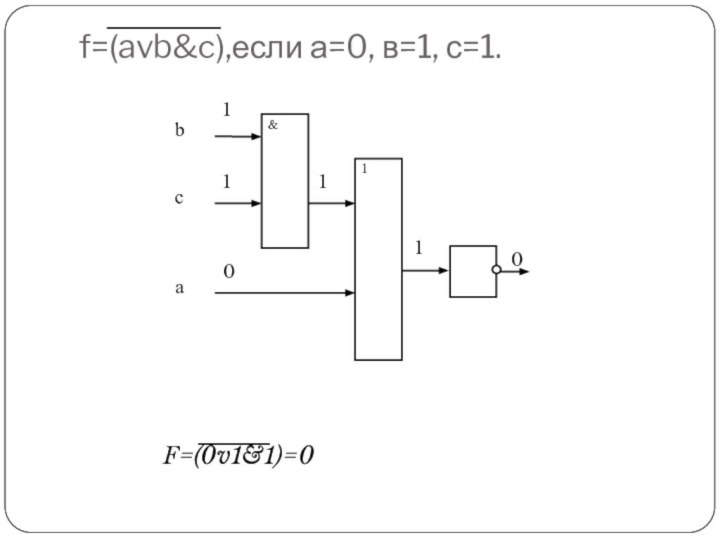
f=(avb&c),если а=0, в=1, с=1.
&
b
с
а
0
1
1
1
1
0
Слайд 17
Составить логическое выражение по соответствующей логической схеме
Слайд 18
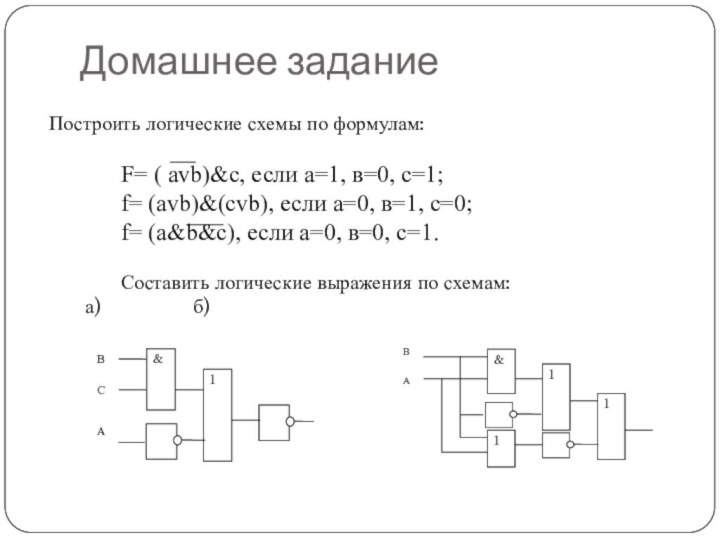
Домашнее задание
Построить логические схемы по формулам:
F= ( avb)&c,
если а=1, в=0, с=1;
f= (avb)&(cvb), если а=0, в=1, с=0;
f=
(a&b&c), если а=0, в=0, с=1.
Составить логические выражения по схемам:
а) б)
Слайд 19
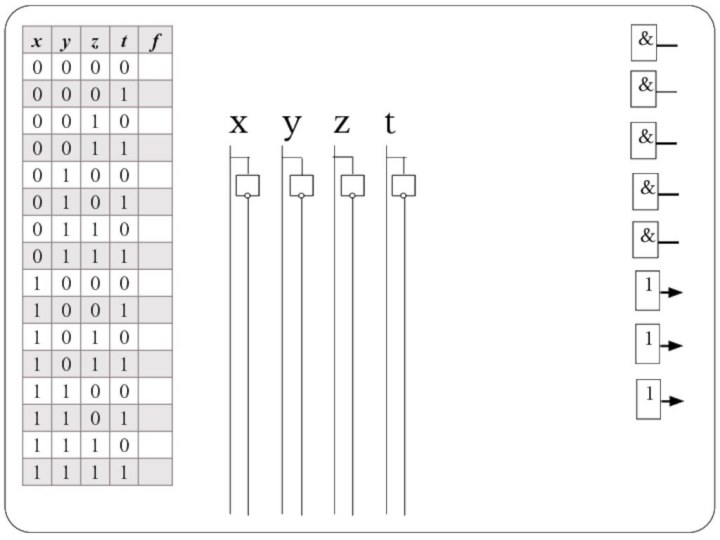
Построить логическую схему для функции f(x,y.z,t)
f(x,y.z,t)=
zt
zt
zt
zt
xy
Слайд 21
Логический элемент, реализующий логическую функцию «стрелка Пирса», называется
элемент Пирса. Он имеет, как минимум, два входа.
Если хотя
бы на один вход поступает сигнал 1, то на выходе будет сигнал 0.
Рис . Условные обозначения логического элемента ИЛИ-НЕ
Элемент Пирса
Слайд 22
Реализация конъюнкции, дизъюнкции, отрицания
на элементах Пирса
x1 = x1
+ x1 = x1 ↓ x1
x1 & x2 =
x1 & x2 = x1 + x2 = (x1 ↓ x1) ↓ (x2 ↓ x2)
x1 ↓ x2 = x1 & x2 или x1 ↓ x2 = x1 + x2
x1 + x2 = x1 + x2 = x1 ↓ x2 = (x1 ↓ x2) ↓ (x1 ↓ x2)
x1
x1 & x2
x1
x2
x1 + x2
x1
x2
Слайд 23
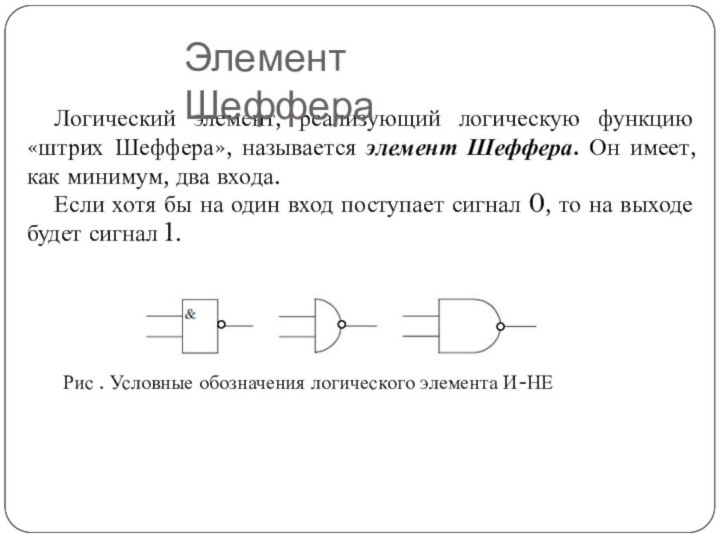
Логический элемент, реализующий логическую функцию «штрих Шеффера», называется
элемент Шеффера. Он имеет, как минимум, два входа.
Если хотя
бы на один вход поступает сигнал 0, то на выходе будет сигнал 1.
Рис . Условные обозначения логического элемента И-НЕ
Элемент Шеффера
Слайд 24
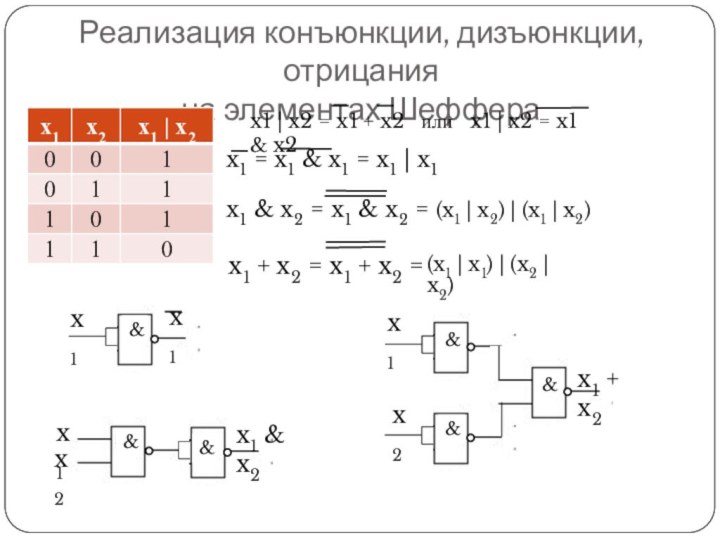
Реализация конъюнкции, дизъюнкции, отрицания
на элементах Шеффера
x1 = x1
& x1 = x1 | x1
x1 & x2 =
x1 & x2 = (x1 | x2) | (x1 | x2)
x1 | x2 = x1 + x2 или x1 | x2 = x1 & x2
x1 + x2 = x1 + x2 =
x1
x1 & x2
x1
x2
x1 + x2
x1
x2
&
&
&
&
&
(x1 | x1) | (x2 | x2)
&
Слайд 25
Логический элемент ИСКЛ-ИЛИ
Логический элемент, реализующий логическую функцию Сложение
по модулю 2 (Исключающее ИЛИ, неравнозначность называется элемент Исключающее
ИЛИ. Он имеет, как минимум, два входа.
Если сигнал 1 поступает на четное количество входов, то на выходе будет сигнал 0.
Если сигнал 1 поступает на нечетное количество входов, то на выходе будет сигнал 1.
Рис . Условные обозначения логического элемента ИЛИ-НЕ
Слайд 26
Функциональные схемы основных узлов ЭВМ.
Логические основы ЭВМ
Слайд 27
Функциональные схемы основных узлов ЭВМ.
Сумматор
Слайд 28
Сумматор
Двоичными сумматорами называют логические устройства, выполняющие операцию сложения
двух чисел, представленных в двоичном коде.
В цифровых устройствах применяются
одноразрядные суммирующие схемы на два и три входа, причем первую называют полусумматором, вторую - полным одноразрядным сумматором.
Полусумматор применяется для выполнения сложения только в разряде с весом 20 (в разряде единиц).
Слайд 29
Полусумматор
Таблицу истинности полусумматора можно получить из правил суммирования
двоичных чисел.
Обозначения:
Входы A и B - одноразрядные
числа, стоящие в разряде единиц;
Выходы: S – сумма; P - перенос в следующий разряд;
0
1
1
0
0
0
0
1
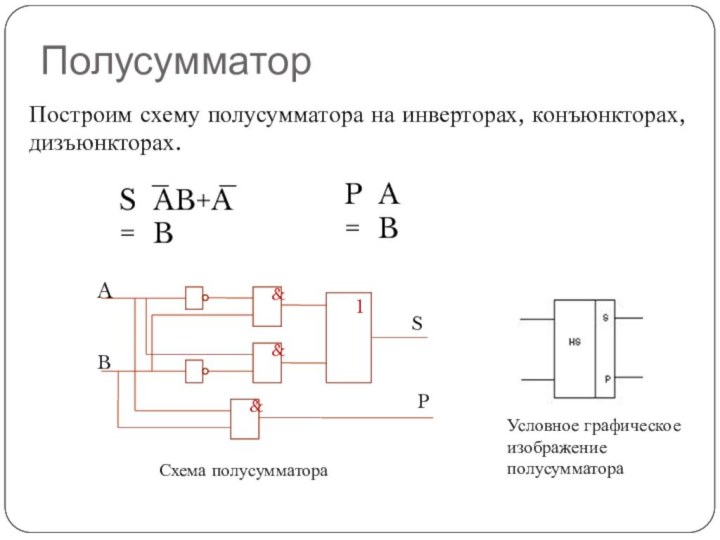
AB+AB
S=
P=
AB
Слайд 30
Построим схему полусумматора на инверторах, конъюнкторах, дизъюнкторах.
Полусумматор
&
&
1
&
A
B
S
P
Схема полусумматора
Условное
графическое изображение полусумматора
Слайд 31
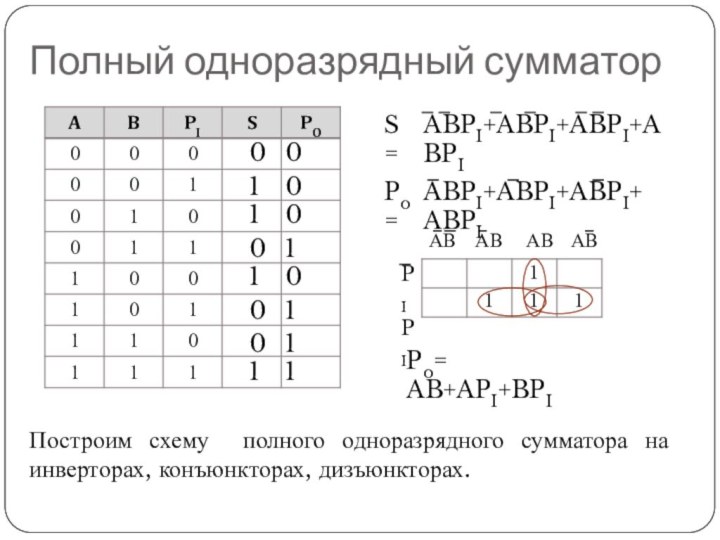
Полный одноразрядный сумматор
Для суммирования во всех двоичных разрядах
(за исключением разряда единиц) используются полные одноразрядные сумматоры.
Они
имеют три входа:
A и B - одноразрядные числа;
PI – перенос из предыдущего разряда (I - сокращение от input – вход).
И два выхода:
S – сумма;
PO – перенос в следующий разряд (O - сокращение от output – выход).
Слайд 32
Полный одноразрядный сумматор
0 0
1 0
1 0
1 1
1 0
0 1
0 1
0 1
S=
Po=
AB AB
AB AB
PI
PI
1
1
1
1
Po= AB+API+BPI
Построим схему полного одноразрядного
сумматора на инверторах, конъюнкторах, дизъюнкторах.
Слайд 33
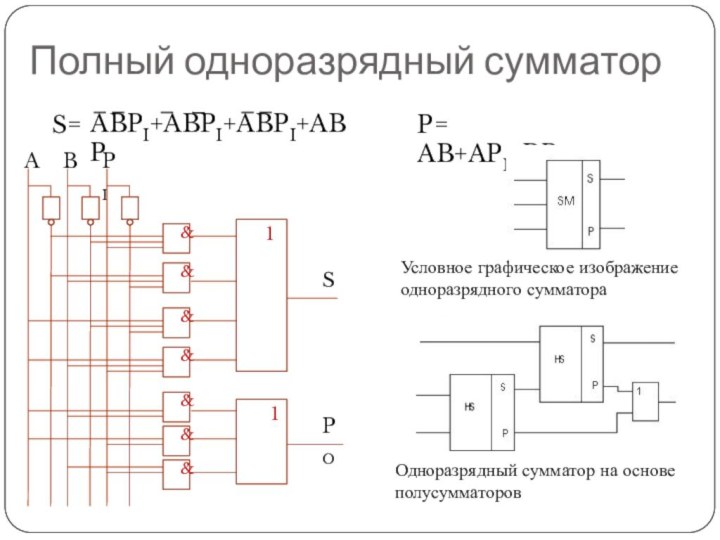
P= AB+API+BPI
Полный одноразрядный сумматор
PI
B
A
Слайд 34
P= AB+API+BPI
Полный одноразрядный сумматор
1
1
PI
B
A
S
PO
Условное графическое изображение одноразрядного сумматора
Одноразрядный
сумматор на основе полусумматоров
Слайд 35
Многоразрядный сумматор
Определенным образом соединяя полусумматоры и полные одноразрядные
сумматоры друг с другом, получают устройства, одновременно выполняющие сложение
нескольких двоичных разрядов – многоразрядные сумматоры.
Полный двоичный n-разрядный сумматор
Слайд 36
Многоразрядный сумматор
Определенным образом соединяя полусумматоры и полные одноразрядные
сумматоры друг с другом, получают устройства, одновременно выполняющие сложение
нескольких двоичных разрядов – многоразрядные сумматоры.
Полный двоичный четырехразрядный сумматор
HS
Слайд 37
Функциональные схемы основных узлов ЭВМ.
Шифраторы и дешифраторы
Слайд 38
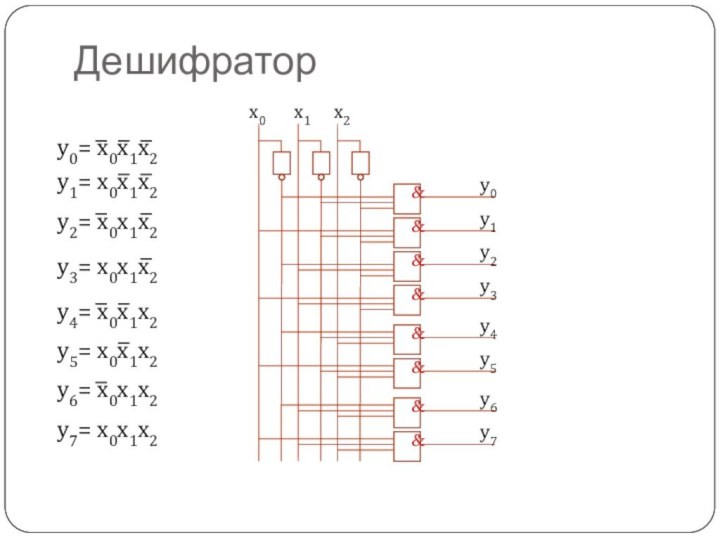
Дешифратор
Дешифратор – логическая схема, содержащая n входов и
2n выходов и преобразующая n-разрядное двоичное слово в соответствующий
управляющий сигнал, который возникает только на одном из его выходов.
Пример трехразрядного дешифратора.
Слайд 39
Дешифратор
x2
x1
x0
y0
y1
y2
y3
y4
y5
y6
y7
Слайд 40
Функциональные схемы основных узлов ЭВМ.
Триггер
Слайд 41
Триггеры
Триггер –логическая схема с памятью.
Термин «триггер» происходит от
английского слова trigger – защелка, спусковой крючок.
Триггер – электронное
устройство, с помощью которого можно записывать, хранить и считывать двоичную информацию.
Триггер широко применяется в регистрах компьютера для запоминания одного разряда двоичного кода.
Слайд 42
Триггер имеет два устойчивых состояния, одно из которых
соответствует логической единице, а другое – логическому нулю.
Под
воздействием сигналов, подаваемых на входы, триггер скачкообразно переходит из одного устойчивого состояния в другое.
Триггеры
Слайд 43
Если хотя бы с оного входа информация в
триггер заносится принудительно под воздействием синхронизирующего сигнала, то триггер
называется синхронизируемым.
Если занесение информации в триггер с любого входа производится без синхронизирующего сигнала, то триггер называется асинхронным.
Триггеры
Слайд 44
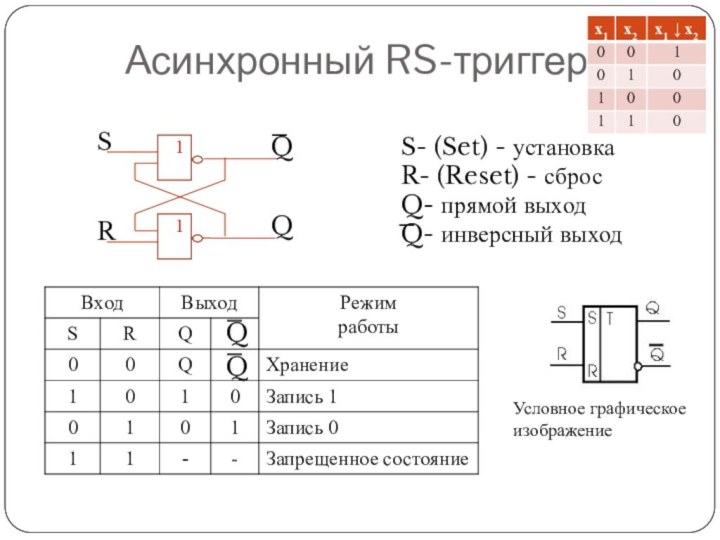
Асинхронный RS-триггер
S
R
Q
S- (Set) - установка
R- (Reset) - сброс
Q-
прямой выход
Q- инверсный выход
Условное графическое изображение
Слайд 45
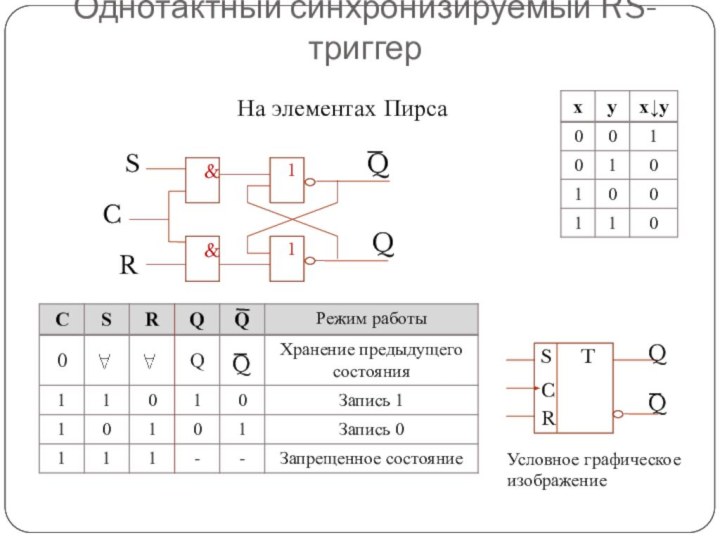
Однотактный синхронизируемый RS-триггер
S
R
Q
C
На элементах Пирса
S
R
C
Q
Условное графическое изображение
T
Слайд 46
Однотактный синхронизируемый RS-триггер
На элементах Шеффера
S
R
Q
C
Слайд 47
S
R
Q
C
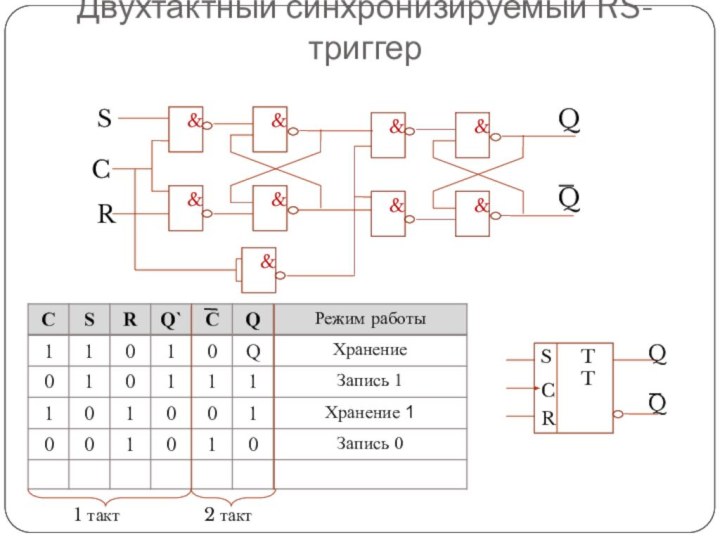
Двухтактный синхронизируемый RS-триггер
S
R
C
Q
TT
1 такт
2 такт
Слайд 48
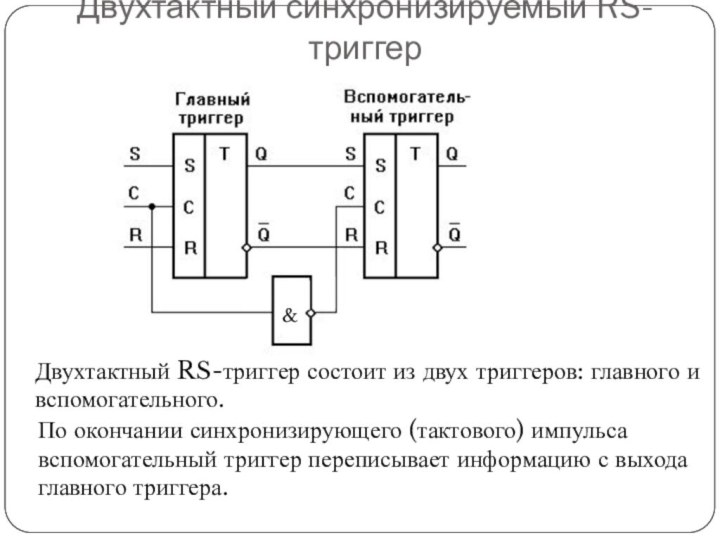
Двухтактный RS-триггер состоит из двух триггеров: главного и вспомогательного.
По окончании синхронизирующего (тактового) импульса вспомогательный триггер переписывает информацию
с выхода главного триггера.
Двухтактный синхронизируемый RS-триггер
&
Слайд 49
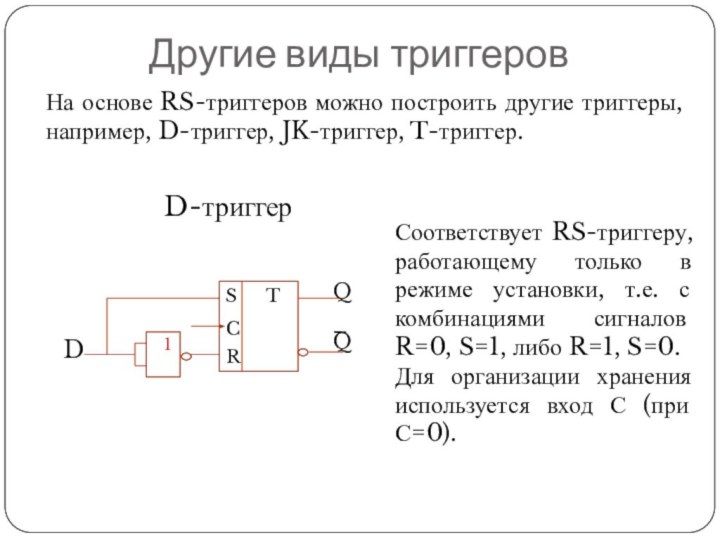
Другие виды триггеров
На основе RS-триггеров можно построить другие
триггеры, например, D-триггер, JK-триггер, T-триггер.
D-триггер
Соответствует RS-триггеру, работающему только в
режиме установки, т.е. с комбинациями сигналов R=0, S=1, либо R=1, S=0.
Для организации хранения используется вход С (при С=0).
Слайд 50
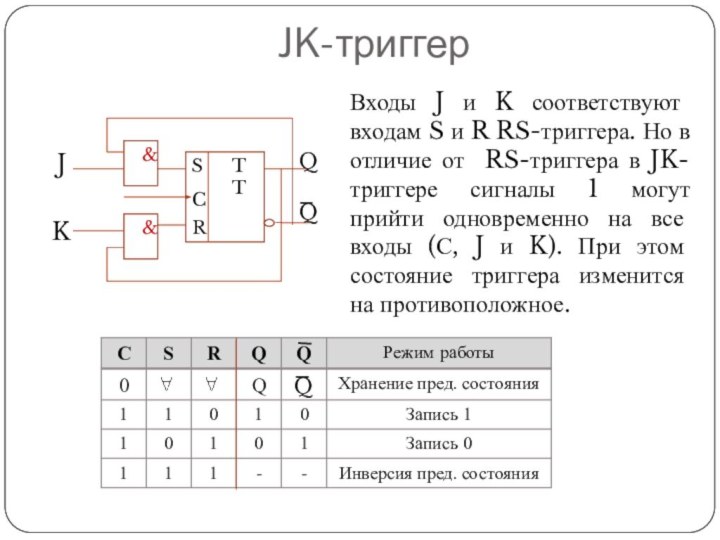
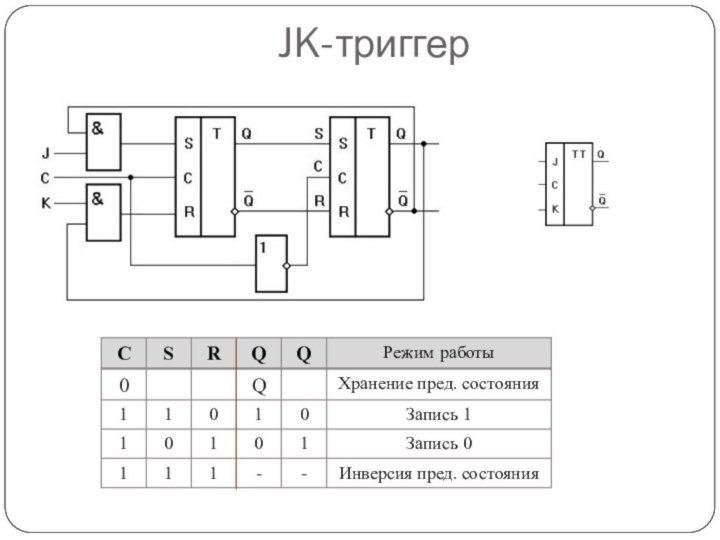
JK-триггер
Входы J и K соответствуют входам S и
R RS-триггера. Но в отличие от RS-триггера в JK-триггере
сигналы 1 могут прийти одновременно на все входы (С, J и K). При этом состояние триггера изменится на противоположное.
Слайд 52
Регистры
Регистры предназначены для хранения и преобразования многоразрядных двоичных
чисел. Для запоминания отдельных разрядов числа могут применяться триггеры
различных типов. Одиночный триггер можно считать одноразрядным регистром.
Занесение информации в регистр называется операцией записи. Операция выдачи информации из регистра – считывание.
Перед записью информации в регистр, его необходимо обнулить.
Слайд 53
Классификация регистров по способу ввода/вывода информации
параллельные (регистры хранения)
– информация вводится и выводится одновременно по всем разрядам;
последовательные
(регистры сдвига) – информация бит за битом «проталкивается» через регистр и выводится также последовательно;
комбинированные – параллельный ввод и последовательный вывод (и наоборот).
Слайд 54
Параллельный регистр
Для записи информации в регистр на его
входных выводах (D0-D3) нужно установить логические уровни, после чего
на вход синхронизации (C) подать разрешающий импульс — логическую единицу.
После этого на выходах Q0-Q3
появится записанное слово.
Регистры запоминают входные сигналы только в момент времени, определяемый сигналом синхронизации.
Схема параллельного регистра
Слайд 55
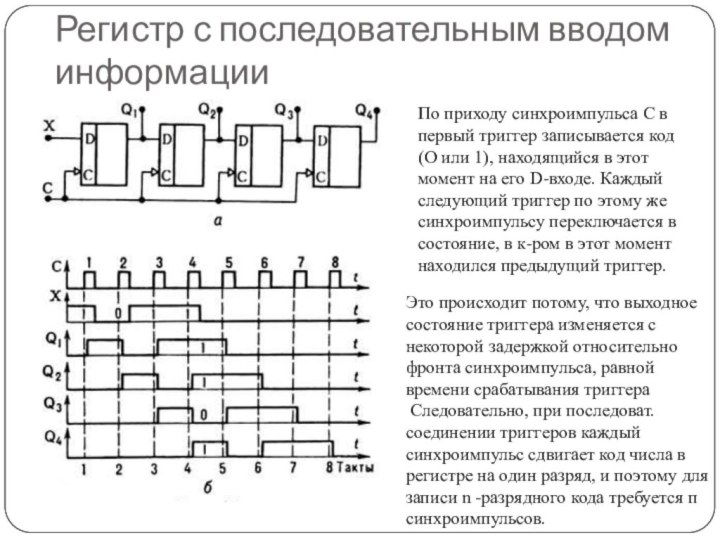
Регистр с последовательным вводом информации
По приходу синхроимпульса С
в первый триггер записывается код (О или 1), находящийся в этот
момент на его D-входе. Каждый следующий триггер по этому же синхроимпульсу переключается в состояние, в к-ром в этот момент находился предыдущий триггер.
Это происходит потому, что выходное состояние триггера изменяется с некоторой задержкой относительно фронта синхроимпульса, равной времени срабатывания триггера
Следовательно, при последоват. соединении триггеров каждый синхроимпульс сдвигает код числа в регистре на один разряд, и поэтому для записи n -разрядного кода требуется п синхроимпульсов.
Слайд 56
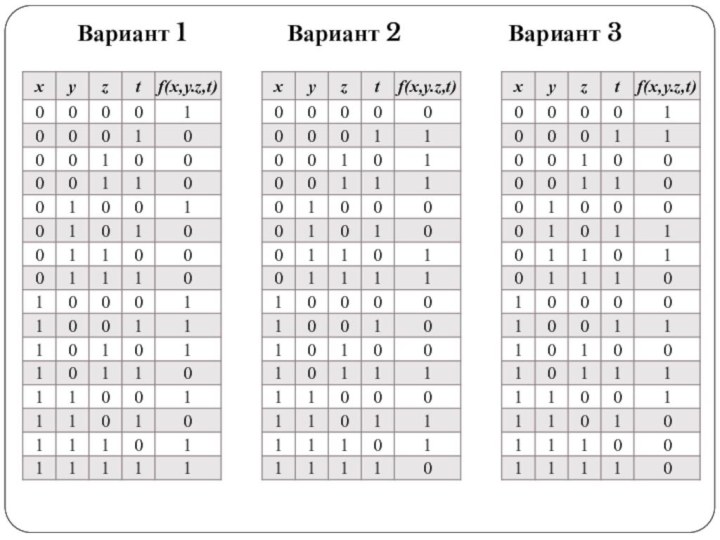
Самостоятельная работа
Вариант 1
Шеффера
Вариант 2
Пирса
Вариант 3
Шеффера
Упростить функцию аналитически и
построить для нее логическую схему на элементах
Для функции 4-х
переменных найти СДНФ, упростить с помощью карт Карно и построить логическую схему на элементах «И», «ИЛИ», «НЕ»
Вариант 1
RS-триггера на элементах Пирса
Вариант 2
RS-триггера на
эл-тах Шеффера
Вариант 3
Асинхронного RS-триггера
Начертить схему и описать работу
Слайд 57
Самостоятельная работа
Вариант 1
Шеффера
Вариант 2
Пирса
Вариант 3
Шеффера
Упростить функцию аналитически и
построить для нее логическую схему на элементах. Построить СДНФ.
Для
функции 4-х переменных найти СДНФ, упростить с помощью карт Карно и построить логическую схему на элементах «И», «ИЛИ», «НЕ»
Построить СПНФ и схему на элементах «исключающее ИЛИ» для данной функции. Построить СКНФ.
Вариант 1
Вариант 2
Вариант 3