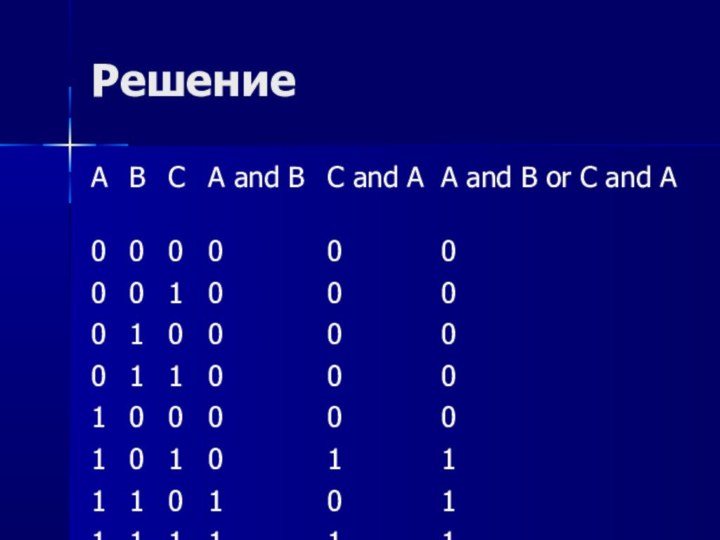
латинскими буквами.
Каждому логическому высказыванию ставится в соответствие логическая переменная,
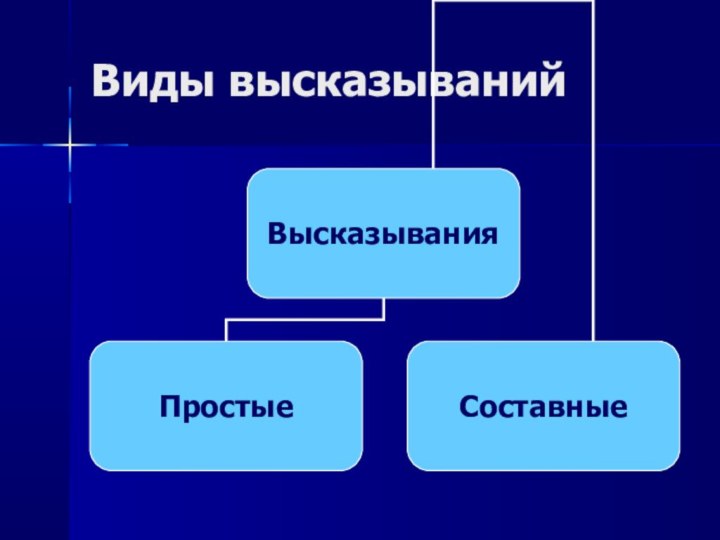
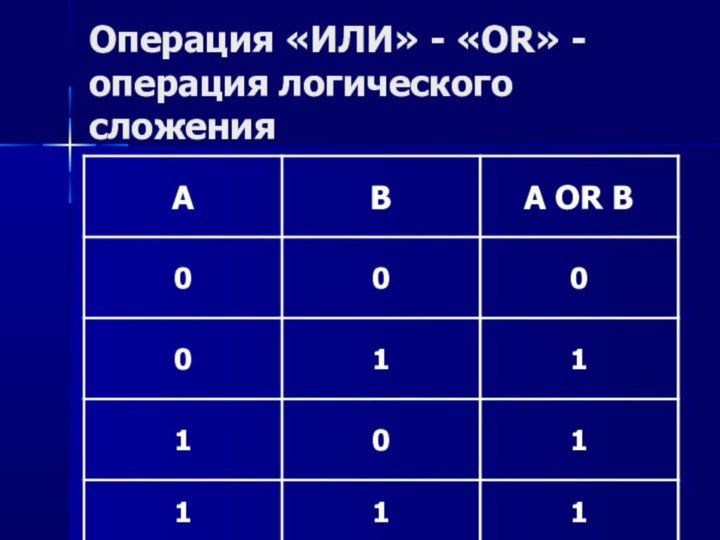
которое принимает значение «истина» или «ложь». А=1 – истина, В=0 – ложь.Составные высказывания образуются из простых с помощью союзов «и», «или», которые в алгебре логики заменяются на логические операции.