Слайд 2
Логика
ЛОГИКА — это наука о формах и законах
человеческого мышления и, в частности, о законах доказательных рассуждений.
Логика изучает мышление как средство познания объективного мира. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира.
Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике (построение компьютеров основано на законах математической логики).
В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.
Слайд 3
АЛГЕБРА ВЫСКАЗЫВАНИЙ
В основе работы логических схем и устройств
персонального компьютера лежит специальный математический аппарат - математическая логика.
Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.
Английский математик Джордж Буль (1815 — 1864 г.) создал логическую алгебру, в которой высказывания обозначены буквами. Сочинение Джорджа Буля, в котором подробно исследовалась эта алгебра, было опубликовано в 1854 г. Оно называлось «Исследование законов мысли» («Investigation of the Laws of Thought»). Отсюда ясно, что Буль рассматривал свою алгебру как инструмент изучения законов человеческого мышления, то есть законов логики.
Алгебру логики иначе называют алгеброй высказываний. В математической логике суждения называются высказываниями.
Слайд 4
ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно
сказать, что оно истинно или ложно.
Например:
Земля - планета
Солнечной системы. (Истинно)
2+8<5 (Ложно)
5 · 5=25 (Истинно)
Всякий квадрат есть параллелограмм (Истинно)
Каждый параллелограмм есть квадрат (Ложно)
2 · 2 =5 (Ложно)
Не всякое предложение является высказыванием:
1) Восклицательные и вопросительные предложения высказываниями не являются.
- “Какого цвета этот дом?”
- “Пейте томатный сок!”
- “Стоп!”
2) Не являются высказываниями и определения.
“Назовем медианой отрезок, соединяющий вершину треугольника с серединой противоположной стороны”.
Определения не бывают истинными или ложными, они лишь фиксируют принятое использование терминов.
3) Не являются высказываниями и предложения типа “Он сероглаз” или
“х- 4х + 3=0” - в них не указано о каком человеке идет речь или для какого числа х верно равенство. Такие предложения называются высказывательными формами.
Слайд 5
Высказывания могут быть простыми и сложными.
Высказывание считается простым,
если никакую его часть нельзя рассматривать как отдельное высказывание
Некоторые
высказывания можно разложить на отдельные части, при этом каждая такая часть будет самостоятельным высказыванием.
Например, высказывание “Сегодня в 4 часа дня я был в школе, а к 6 часам вечера пошел на каток” состоит из 2 частей.
Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым.
Слайд 6
Практическое задание
Определи, какие из перечисленных фраз является высказываниями:
Обязательно
займись каким-либо видом спорта;
Переводчик должен знать хотя бы
два языка;
Ты играешь в хоккей?
Два больше трех.
Земля – планета Солнечной системы.
Каждый параллелограмм является квадратом.
Волга впадает в каспийское море.
В феврале 30 дней.
Остров – это часть суши, со всех сторон окруженная водой.
Все девочки любят играть в куклы.
Слайд 7
Практическое задание
Какие из следующих высказываний являются истинными, а
какие ложными?
1. Город Москва – столица России.
2.
Число 12 – простое.
3. 7*3=1.
4. 12<15.
5. Сканер – устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.
6. Клавиатура – устройство ввода информации.
Слайд 8
Сложное высказывание получается путем объединения простых высказываний логическими
связками — НЕ, И, ИЛИ. Значение истинности сложных высказываний
зависит от истинности входящих в них простых высказываний и объединяющих их связок.
Например, даны простые высказывания:
На улице идет дождь.
На улице светит солнце.
На улице пасмурная погода.
Составим из них сложные высказывания:
На улице идет дождь и на улице светит солнце.
На улице светит солнце или на улице пасмурная погода.
Неверно что на улице идет дождь.
Слайд 9
Практическое задание
Из двух простых высказываний постройте сложное высказывание,
используя связку "И", "ИЛИ":
Например:
Все ученики изучают математику
Все ученики
изучают литературу=> Все ученики изучают математику и литературу
1) Марина старше Светы. Оля старше Светы.
2) Одна половина класса изучает английский язык. Вторая половина класса изучает немецкий язык.
3) В кабинете есть учебники. В кабинете есть справочники.
4) Часть туристов любит чай. Остальные туристы любят молоко
Слайд 10
В математической логике не рассматривается конкретное содержание высказывания,
важно только, истинно оно или ложно. Поэтому высказывание можно
представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0.
Простые высказывания назвали логическими переменными и для простоты записи их обозначают латинскими буквами: А, В, С…
Луна является спутником Земли. А = 1
Москва – столица Германии. В = 0
Сложные высказывания называются логическими функциями. Значения логической функции также может принимать значения только 0 или 1.
Слайд 11
БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
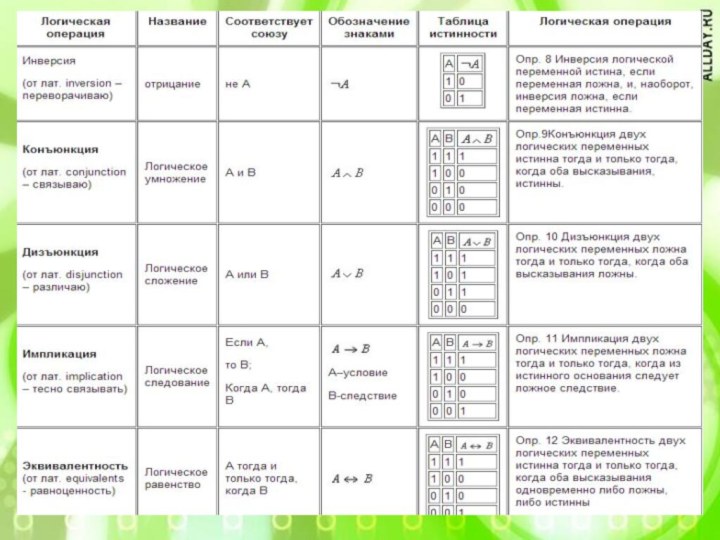
В алгебре высказываний, как и в
обычной алгебре, вводится ряд операций. Логические связки И, ИЛИ
и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.
Слайд 12
Логические операции
Операция отрицания
2) Логическое умножение (конъюнкция)
3)
Логическое сложение (дизъюнкция)
Слайд 13
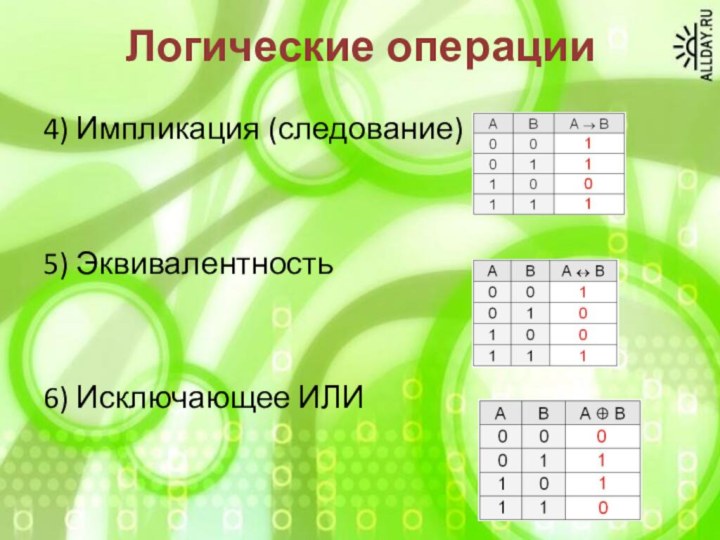
Логические операции
4) Импликация (следование)
5) Эквивалентность
6) Исключающее ИЛИ
Слайд 15
1. Отрицание
2. Скобки
3. Умножение, Импликация, эквивалентность
4. Сложение
Приоритет операций
Слайд 16
Практическое задание
Найдите значения логических выражений:
1
2
3
4
5
6
7
8
9
Слайд 17
Практическое задание
Пусть А= "это утро ясное", а В=
"это утро теплое". Выразите следующие формулы на обычном языке:
Слайд 18
Домашнее задание
1. Даны простые высказывания: А= {15>13}, В={4=5},
C= {7
числа Х логическое выражение не ((Х>15) или (Х<-5)) примет значение:
ложь,
истинна.
Слайд 20
Таблицы истинности
Для каждого составного высказывания можно построить таблицу
истинности, которая определяет истинность или ложность логического выражения при
всех возможных комбинациях исходных значений простых высказываний.
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий:
1) записать выражение и определить порядок выполнения операций
2) определить количество строк в таблице истинности (определяется по формуле Q =2n, где n - количество входных переменных)
3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций)
4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных.
5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности
Слайд 21
Например, построим таблицу истинности для логической функции:
1. Количество
входных переменных в заданном выражении равно трем (A,B,C). Значит,
количество входных наборов, а значит и строк Q=23=8.
2. Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов и (B V C), а также искомого окончательного значения сложного арифметического выражения