Слайд 2
Команды проверки условий.
Эти команды проверяют, свободен ли
путь для Робота в каждом из четырёх возможных направлений:
Например:
если
справа свободно то
вправо
закрасить
все
сверху свободно
снизу свободно
слева свободно
справа свободно
Слайд 3
В одном условии можно использовать несколько команд проверки
условий, применяя логические связки и, или, не, например:
если (справа свободно) и
(не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Слайд 4
Выполните задание
На бесконечном поле есть горизонтальная и вертикальная
стены. Правый конец горизонтальной стены соединён с верхним концом
вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно под горизонтальной стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно ниже горизонтальной стены и левее вертикальной стены. Проходы должны остаться незакрашенными.
Робот должен закрасить только клетки, удовлетворяющие данному условию.
Слайд 5
Пояснение.
Следующий алгоритм выполнит требуемую задачу.
Алг
нач
нц пока не
сверху свободно
закрасить
вправо
кц
нц пока сверху свободно
вправо
кц
нц пока справа свободно
закрасить
вправо
кц
нц пока
не справа свободно
закрасить
вниз
кц
нц пока справа свободно
вниз
кц
нц пока не справа свободно
закрасить
вниз
кц
кон
Слайд 6
Решите самостоятельно:
1). Напишите для Робота алгоритм, закрашивающий все
клетки, расположенные левее первого и ниже второго отрезков стены
и ниже четвёртого и левее пятого отрезков стены. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен.
Слайд 7
2). На бесконечном поле имеется лестница. Сначала лестница

спускается вниз слева направо, потом поднимается вверх также слева
направо. После подъема лестница переходит в вертикальную стену. Высота каждой ступени — 1 клетка, ширина — 1 клетка. Количество ступенек, ведущих вверх, и количество ступенек, ведущих вниз, неизвестно. Между спуском и подъемом ширина площадки — 1 клетка. Робот находится в клетке, расположенной в начале спуска. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р») .
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над лестницей, как показано на рисунке. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.
Слайд 8
3). На бесконечном поле есть горизонтальная и вертикальная

стены. Правый конец горизонтальной стены соединён с нижним концом
вертикальной стены. Длины стен неизвестны. В горизонтальной стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно над горизонтальной стеной у её правого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно левее и правее вертикальной стены. Проход должен остаться незакрашенным. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки(см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера прохода внутри стены.
Слайд 9
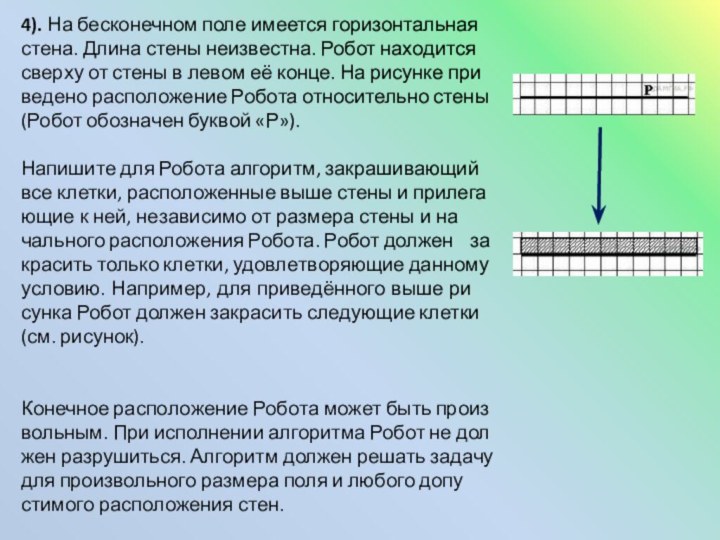
4). На бесконечном поле имеется горизонтальная стена. Длина
стены неизвестна. Робот находится сверху от стены в левом
её конце. На рисунке приведено расположение Робота относительно стены (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные выше стены и прилегающие к ней, независимо от размера стены и начального расположения Робота. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. При исполнении алгоритма Робот не должен разрушиться. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен.
Слайд 10
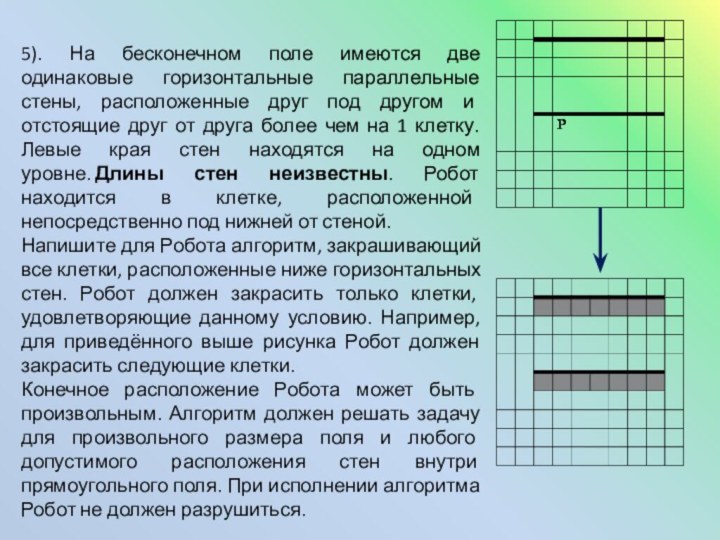
5). На бесконечном поле имеются две одинаковые горизонтальные
параллельные стены, расположенные друг под другом и отстоящие друг
от друга более чем на 1 клетку. Левые края стен находятся на одном уровне. Длины стен неизвестны. Робот находится в клетке, расположенной непосредственно под нижней от стеной.
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные ниже горизонтальных стен. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки.
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.
Слайд 11
6). На бесконечном поле имеются две вертикальные стены
и одна горизонтальная, соединяющая нижний конец левой и верхний
конец правой вертикальных стен. Длины стен неизвестны. Робот находится в клетке, расположенной слева от нижнего края правой вертикальной стены, рядом со стеной.
На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, примыкающие к вертикальным стенам справа. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.