Слайд 2
Кодификатор и спецификация ГИА_2014
Кодификатор:
Раздел 1. Информационные
процессы
Раздел 1.3.3 Логические значения, операции, выражения
Спецификация:
На уровне воспроизведения знаний проверяется такой фундаментальный теоретический материал, как:
……………………………………………………….
основные элементы математической логики;
……………………………………………………….
Слайд 3
Задания ГИА
НЕ (число >50) ИЛИ (число чётное) =
0
0
0
число >50 число
нечётное
Решение:
Ответ: 123
Слайд 6
Кодификатор и спецификация ЕГЭ_2014
Кодификатор:
Раздел 1. Информация
и информационные процессы
1.5.1 Высказывания, логические операции, кванторы,
истинность высказывания
Спецификация:
В КИМ ЕГЭ по информатике не включены задания, требующие простого воспроизведения знания терминов, понятий, величин, правил (такие задания слишком просты для итогового экзамена).
……………………………………………………………………………
формировать для логической функции таблицу истинности и логическую схему;
формулировать запросы к базам данных и поисковым системам.
Слайд 11
Задания ЕГЭ - ГИА
Прослеживается преемственность между заданиями:
№2 и
А3 (Умение применять логические операции НЕ, И, ИЛИ);
№18 и
В12 (поиск в Интернете);
возможно, между №12 и А6 (поиск в базах данных).
Наибольшую сложность представляют задания А10 и В15 (!)
Слайд 12
Задание ЕГЭ А10
Логические операции с утверждениями о множествах
связаны с операциями над множествами (теоретико-множественными операциями).
Пусть А, В
– некоторые множества. Их элементы принадлежат некоторому универсальному множеству U (в зависимости от задачи это может быть, например, множество целых чисел, множество точек на прямой и т.д.). Тогда верно следующее:
Пусть X - произвольный элемент универсального множества U. Тогда следующие высказывания эквивалентны ():
Слайд 13
Задание ЕГЭ А10
2. Пусть А В, т.е.
А – подмножество В, х – произвольный элемент универсального
множества U. Тогда истинно высказывание:
(x A) (x B).
Обратно, пусть высказывание (x A) (x B) истинно при любом x U. Тогда А В.
Обозначения:
A B – пересечение множеств А и В
A B – объединение множеств А и В
U \ A – дополнение множества А до универсального множества U
Слайд 14
Задание ЕГЭ А10
На числовой прямой даны два отрезка:
P = [2, 10] и Q = [6, 14].
Выберите
такой отрезок A, что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17]
Слайд 15
Решение
Преобразуем формулу. По определению,
(F G)
( F \/ G)
Из формулы (1) получаем:
(x
A) \/ (хР) \/ (хQ) (2)
Далее, (хР) \/ (хQ) x(PQ) при любых x, P, Q.
По условию, P = [2,10], Q = [6,14]. Т.о. PQ = [2,14].
Перепишем формулу (2):
(x A) \/ (х[2,14])
Слайд 16
Решение
1) [0, 3] 2) [3, 11] 3) [11,
15] 4) [15, 17]
Вернемся к импликации:
(x A) (х[2,14])
Эта
формула истинна тогда и только тогда, когда принадлежность числа х отрезку А влечет принадлежность числа х отрезку [2,14]. Т.е. отрезок А должен быть подмножеством отрезка [2,14]. Из четырех предложенных отрезков этому условию удовлетворяет только отрезок [3,11].
Ответ: 2
Слайд 17
Задание В15 - одно из самых сложных в
ЕГЭ по информатике!!!
Проверяются умения:
преобразовывать выражения, содержащие логические переменные;
описывать на естественном языке множество значений логических переменных, при которых заданный набор логических переменных истинен;
подсчитывать число двоичных наборов, удовлетворяющих заданным условиям.
Самое сложное, т.к. нет формальных правил, как это сделать, требуется догадка.
Слайд 20
Условные обозначения
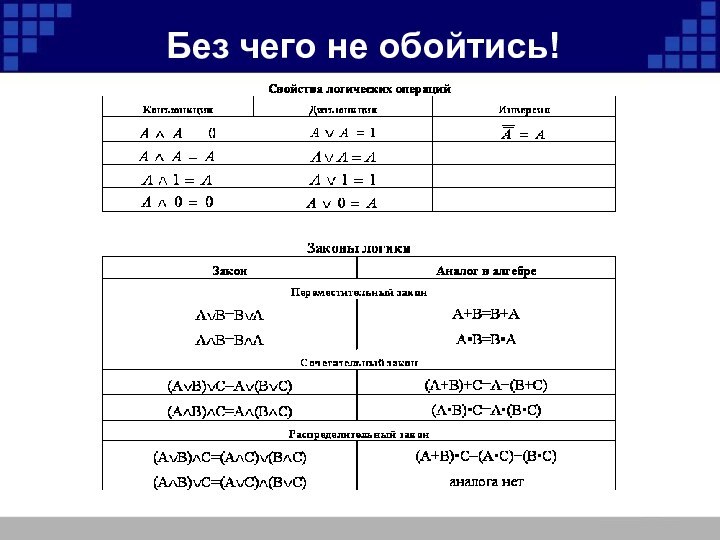
конъюнкция :A /\ B , A
B, AB, А&B, A and B
дизъюнкция: A \/
B , A+ B, A | B, А or B
отрицание: A , А, not A
эквиваленция: A В, A B, A B
исключающее «или»: A B , A xor B
Слайд 21
Метод замены переменных
Сколько существует различных наборов значений логических
переменных х1, х2, …, х9, х10, которые удовлетворяют всем
перечисленным ниже условиям:
((x1 ≡ x2) \/ (x3 ≡ x4)) /\ (¬(x1 ≡ x2) \/ ¬(x3 ≡ x4)) =1
((x3 ≡ x4) \/ (x5 ≡ x6)) /\ (¬(x3 ≡ x4) \/ ¬(x5 ≡ x6)) =1
((x5 ≡ x6) \/ (x7 ≡ x8)) /\ (¬(x5 ≡ x7) \/ ¬(x7 ≡ x8)) =1
((x7 ≡ x8) \/ (x9 ≡ x10)) /\ (¬(x7 ≡ x8) \/ ¬(x9 ≡ x10)) =1
В ответе не нужно перечислять все различные наборы х1, х2, …, х9, х10, при которых выполняется данная система равенств. В качестве ответа необходимо указать количество таких наборов (демо-версия 2012 г.)
Слайд 22
Шаг 1. Упрощаем, выполнив замену переменных
t1 = x1
x2
t2 = x3 x4
t3 = x5 x6
t4 = x7 x8
t5 = x9 x10
После упрощения:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1
(t2 \/ t3) /\ (¬t2 \/ ¬ t3 ) =1
(t3 \/ t4) /\ (¬t3 \/ ¬ t4 ) =1
(t4 \/ t5) /\ (¬t4 \/ ¬ t5 ) =1
Рассмотрим одно из уравнений:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1
Очевидно, оно =1 только если одна из переменных равна 0, а другая – 1. Воспользуемся формулой для выражения операции XOR через конъюнкцию и дизъюнкцию:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) = t1 t2 = ¬(t1 ≡ t2 ) =1
¬(t1 ≡ t2 ) =1
¬(t2 ≡ t3 ) =1
¬(t3 ≡ t4 ) =1
¬(t4 ≡ t5 ) =1
Решение
Слайд 23
Шаг 2. Анализ системы
¬(t1 ≡ t2 ) =1
¬(t2
≡ t3 ) =1
¬(t3 ≡ t4 ) =1
¬(t4 ≡
t5 ) =1
Т.к. tk = x2k-1 ≡ x2k (t1 = x1 x2,….), то каждому значению tk соответствует две пары значений x2k-1 и x2k ,
например:
tk=0 соответствуют две пары - (0,1) и (1,0) ,
а tk=1 – пары (0,0) и (1,1).
Слайд 24
Шаг 3. Подсчет числа решений.
Каждое t имеет 2
решения, количество t – 5. Т.о. для переменных t
существует 25 = 32 решения.
Но каждому t соответствует пара решений х, т.е. исходная система имеет 2*32 = 64 решения.
Ответ: 64
Слайд 25
Метод исключения части решений
Сколько существует различных наборов значений
логических переменных х1, х2, …, х5, y1,y2,…, y5, которые
удовлетворяют всем перечисленным ниже условиям:
(x1→ x2)∧(x2→ x3)∧(x3→ x4)∧(x4→ x5) =1;
( y1→ y2)∧( y2→ y3)∧( y3→ y4)∧( y4→ y5) =1;
y5→ x5 =1.
В ответе не нужно перечислять все различные наборы х1, х2, …, х5, y1,y2,…, y5, при которых выполняется данная система равенств. В качестве ответа необходимо указать количество таких наборов.
Слайд 26
Решение
Первое уравнение – конъюнкция нескольких операций импликации, равна
1, т.е. каждая из импликаций истинна. Импликация ложна только
в одном случае, когда 1 0, во всех других случаях (0 0, 0 1, 1 1) операция возвращает 1. Запишем это в виде таблицы:
Шаг 1. Последовательное решение уравнений
Слайд 27
Шаг1. Последовательное решение уравнений
Т.о. получено 6 наборов решений
для х1,х2,х3,х4,х5:
(00000), (00001), (00011), (00111), (01111), (11111).
Рассуждая аналогично,
приходим к выводу, что для y1, y2, y3, y4, y5 существует такой же набор решений.
Т.к. уравнения эти независимы, т.е. в них нет общих переменных, то решением этой системы уравнений (без учета третьего уравнения) будет 6*6=36 пар «иксов» и «игреков».
Рассмотрим третье уравнение:
y5→ x5 =1
Решением являются пары: 0 0
0 1
1 1
Не является решением пара: 1 0
Слайд 28
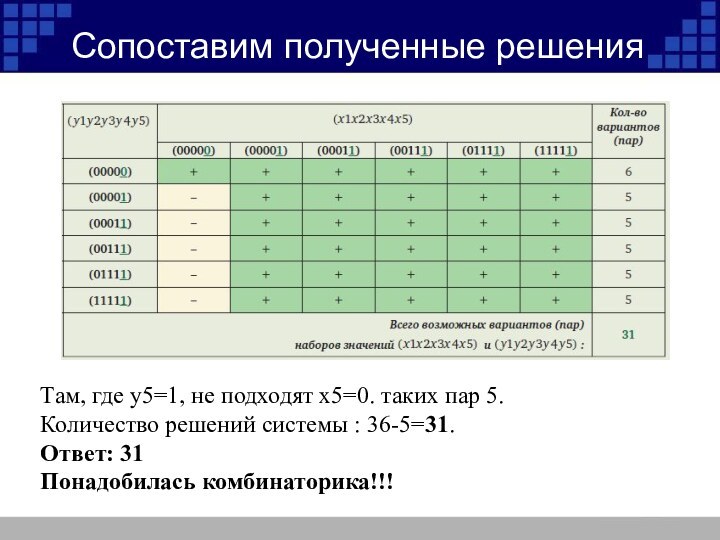
Сопоставим полученные решения
Там, где y5=1, не подходят
x5=0. таких пар 5.
Количество решений системы : 36-5=31.
Ответ:
31
Понадобилась комбинаторика!!!
Слайд 29
Метод динамического программирования
Сколько различных решений имеет логическое уравнение
x1 → x2 → x3 → x4 → x5
→ x6 = 1,
где x1, x2, …, x6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Слайд 30
Решение
Шаг 1. Анализ условия
Слева в уравнении последовательно записаны
операции импликации, приоритет одинаков.
Перепишем:
((((X1 → X2) → X3) →
X4) → X5) → X6 = 1
NB! Каждая следующая переменная зависит не от предыдущей, а от результата предыдущей импликации!
Слайд 31
Шаг 2. Выявление закономерности
Рассмотрим первую импликацию, X1 →
X2. Таблица
истинности:
Из одного 0 получили 2 единицы, а из
1 получили один 0 и одну 1. Всего один 0 и три 1, это результат первой операции.
Слайд 32
Шаг 2. Выявление закономерности
Подключив к результату первой операции
x3 , получим:
Из двух 0 – две 1,
из каждой 1 (их 3) по одному 0 и 1 (3+3)
Слайд 33
Шаг 3. Вывод формулы
Т.о. можно составить формулы для
вычисления количества нулей Ni и количества единиц Ei для
уравнения с i переменными:
,
Слайд 34
Шаг 4. Заполнение таблицы
Заполним слева направо таблицу для
i=6, вычисляя число нулей и единиц по приведенным выше
формулам; в таблице показано, как строится следующий столбец по предыдущему:
:
Ответ: 43
Слайд 35
Метод с использованием упрощений логических выражений
Сколько различных решений
имеет уравнение
((J → K) →(M N
L)) ((M N L) → (¬J K)) (M → J) = 1
где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Слайд 36
Решение
Заметим, что J → K = ¬J
K
Введем замену переменных:
J → K=А, M N
L =В
Перепишем уравнение с учетом замены:
(A → B)(B → A) (M → J)=1
4. (A B) (M → J)=1
5. Очевидно, что A B при одинаковых значениях А и В
6. Рассмотрим последнюю импликацию M → J=1
Это возможно, если:
M=J=0
M=0, J=1
M=J=1
Слайд 37
Решение
Т.к. A B, то
При M=J=0
получаем 1 + К=0. Нет решений.
При M=0,
J=1 получаем 0 + К=0, К=0, а N и L - любые , 4 решения:
¬J K= M N L
Слайд 38
Решение
10. При M=J=1 получаем 0+К=1*N*L, или K=N*L,
4
решения:
11. Итого имеет 4+4=8 решений
Ответ: 8













![Задачи ЕГЭ по информатике Задание ЕГЭ А10На числовой прямой даны два отрезка: P = [2, 10]](/img/tmb/12/1155572/e10aea66dc1047deb7efc38c327a5d92-720x.jpg)

![Задачи ЕГЭ по информатике Решение1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17]Вернемся](/img/tmb/12/1155572/e390178095fbf32f5e9abb9ccd18f9af-720x.jpg)