Презентация на тему Измерение количества информации: Measurement of Information

the information, owns the world. Francis Bacon
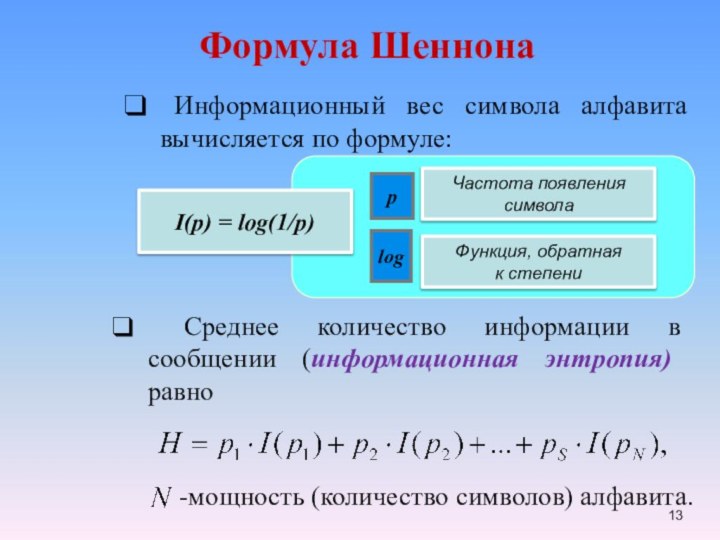
Информация –знания, получаемые

Что такое информация?
What is information?

измеряют в миллиметрах, сантиметрах, метрах, дециметрах…
Массу измеряют в

cold and snowy.
Предложение 2 даёт более полезную
информацию.
Пример 2:

Как можно измерить информацию?
Can we measure information?

определяется независимо от его содержания, воспринимая текст как последовательность

Количество информации в тексте связывается с содержанием текста, учитывая вероятности его символов.

Хартли в 1928 году.
First attempt to quantify information

1:
In winter is cold. (18 символов)
In winter is cold

вес – несёт фиксированное количество информации.
Все символы

K

i

I = K i

Количество символов
в сообщении

Информационный вес символа алфавита



символов. Какое количество информации оно несёт?
Формула Хартли
Решение:
N = 32

Ответ: 90 битов (28 5 = 140(битов) для сообщения из 28 символов).

I = K i,
N = 2i

32 = 2i, i = 5, I = 18 5 = 90 (битов)





Английский алфавит содержит 26 букв. Для записи текста нужны пробел, точка, запятая, вопросительный знак, восклица-тельный знак, тире. Получается расши-ренный алфавит мощностью в 32 символа.



пример 1

предложениях примера 2:
Tomorrow will be cold and snowy. (32

пример 2



энтропия) равно
Информационный вес символа алфавита вычисляется по формуле:

I(p) = log(1/p)

p

log

Частота появления
символа

Функция, обратная
к степени

-мощность (количество символов) алфавита.

равно
3.753 бит,
количество информации во
втором сообщении равно

пример 2

и математик Клод Шеннон в 1948 году в статье

К. Шеннон первым предложил использовать термин «бит» для обозначения

large measure to Shannon's insights, digital systems have come

символов. Какова мощность алфавита, с помощью которого записано это

Задача

Решение:
I = 720
K = 180
N – ?

Ответ: 16 символов.

N = 2 i,
I = K i,
i = I/K

i = 720/180 = 4 (бита);
N = 24 = 16 (символов)



(LAT) буквы
цифры (1, 2, 3, 4, 5, 6,

Алфавит содержит 256 символов.
256 = 28  i=8

1 байт - информационный вес символа алфавита мощностью 256.

1 байт = 8 битов

1 килобайт = 1 Кб = 1024 байта = 210 байтов
1 мегабайт = 1 Мб = 1024 Кб = 210 Кб = 220 байтов
1 гигабайт = 1 Гб = 1024 Мб = 210 Мб = 220 Кб = 230 байтов
1 терабайт = 1 Тб = 1024 Гб = 210 Гб = 220 Мб = 230 Кб = 240 байтов

4096 символов. Каков информационный вес символа этого сообщения? Сколько

I = 4 Кб,
K = 4096;
i – ? N – ?

Ответ: информационный вес символа = 8,
алфавит содержит 256 символов.

N = 28 = 256 (символов)

Решение:

информации в байтах содержат 10 страниц текста, если на

Решение:
N=64, i=6, K=10  32  64= 20 480 (символов)

Ответ: 15360 байтов.

I= K  i / 8 = 20480  6 / 8 = 15360 (байтов)

Задача

Упражнение 5