- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку информатики Логические основы работы компьютера, 10 класс
Содержание
- 2. Ключевые понятия изучения темы:Основные понятия алгебры логикиВысказываниеЛогическое отрицаниеЛогическое сложениеЛогическое умножениеИмпликацияЭквиваленцияТаблицы истинности
- 3. Логика - наука, изучающая законы и формы
- 4. ВЫСКАЗЫВАНИЕЗадание: Объясните, почему следующие предложения не являются
- 5. Высказывания Простое высказывание (логическая переменная)содержит только одну
- 6. Основные логические операцииОтрицание (инверсия), от лат. inversio
- 7. Логическое сложение (дизъюнкция), от лат.
- 8. Логическое умножение (конъюнкция), от лат.
- 9. ДРУГИЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИИмпликация (логическое следование), от лат.
- 10. Эквиваленция (равнозначность), от лат. Aequivalens - равноценное:соответствует
- 11. ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙОПЕРАЦИЯ В СКОБКАХ;ОТРИЦАНИЕ;ЛОГИЧЕСКОЕ УМНОЖЕНИЕ;ЛОГИЧЕСКОЕ СЛОЖЕНИЕ;ИМПЛИКАЦИЯ;ЭКВИВАЛЕНЦИЯ.
- 12. ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ Построение таблиц истинности: определить
- 13. ЗАДАНИЯ:
- 14. Скачать презентацию
- 15. Похожие презентации













Слайд 2
Ключевые понятия изучения темы:
Основные понятия алгебры логики
Высказывание
Логическое отрицание
Логическое
сложение
Слайд 3
Логика - наука, изучающая законы и формы
мышления.
Этапы
развития логики:
I этап - формальная логика. Основатель — Аристотель
(384-322 гг. до н.э.), ввел основные формы абстрактного мышления.II этап - математическая логика. Основатель -немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений. /77 этап - математическая логика (булева алгебра). Основатель - английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.
Алгебра логики - это математический аппарат, с
помощью которого записывают (кодируют), упрощают,
вычисляют и преобразовывают логические
высказывания.
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Слайд 4
ВЫСКАЗЫВАНИЕ
Задание:
Объясните, почему следующие предложения не являются высказываниями:
а)
Уходя гасите свет.
б) Какого цвета этот дом?
в) Посмотрите в
окно.Задание:
Придумайте несколько высказываний:
Задание:
Придумайте 2-3 предложения, которые не являются высказываниями:
Высказывание - повествовательное предложение, о котором можно сказать, истинно оно или ложно.
Высказывание может принимать только одно из двух логических значений - истинно (/) или ложь (0).
Примеры: Земля - планета Солнечной системы (истинное высказывание).
3 + б > 10 (ложное высказывание).
Слайд 5
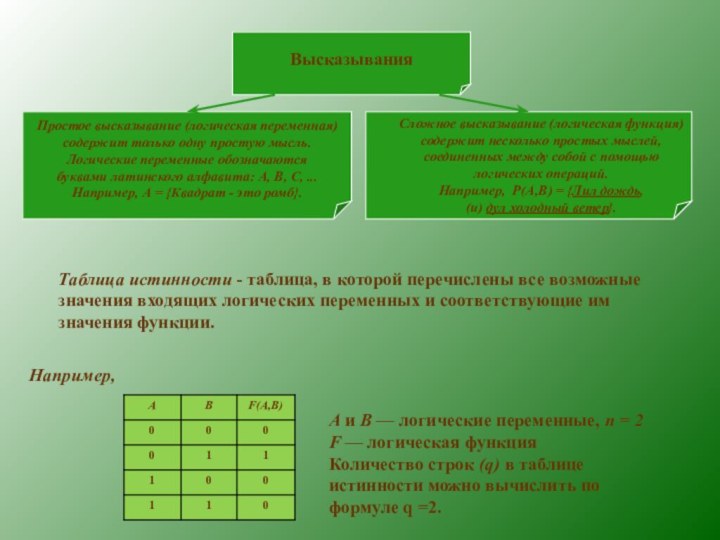
Высказывания
Простое высказывание (логическая переменная)
содержит только одну простую
мысль.
Логические переменные обозначаются
буквами латинского алфавита: А, В,
С, ... Например, А = {Квадрат - это ромб}.
Сложное высказывание (логическая функция)
содержит несколько простых мыслей,
соединенных между собой с помощью
логических операций.
Например, Р(А,В) = {Лил дождь,
(и) дул холодный ветер}.
Таблица истинности - таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
Например,
А и В — логические переменные, п = 2
F — логическая функция
Количество строк (q) в таблице истинности можно вычислить по формуле q =2.
Слайд 6
Основные логические операции
Отрицание (инверсия), от лат. inversio -
переворачиваю:
соответствует частице НЕ, словосочетанию НЕВЕРНО, ЧТО;
обозначение: не А, А,
- А;таблица истинности:
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Слайд 7
Логическое сложение (дизъюнкция), от лат. disjunctio
- различаю:
соответствует союзу ИЛИ;
обозначение: +, или, V;
таблица истинности:
Дизъюнкция ложна
тогда и только тогда, когда оба высказывания ложны.
пример: F = {На улице светит солнце или дует сильный ветер};
Слайд 8
Логическое умножение (конъюнкция), от лат. vincire
- cвязываю:
соответствует союзу И
(в естественном языке: и А, и
В; как А, так и В;А вместе с В; А, несмотря на В А, в то время как В);обозначение: х, •, &, и, ^, and;
таблица истинности:
Конъюнкция истинна тогда и только тогда, когда оба высказывания
истинны.
Пример: F={На улице светит солнце и
дует сильный ветер};
Слайд 9
ДРУГИЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Импликация (логическое следование), от лат. implication
- тесно
связываю:соответствует речевому обороту ЕСЛИ ...ТО (в естественном языке: если А, то В; В, если А;
В необходимо для А; А достаточно для В;
А только тогда, когда В; В тогда, когда А; Все А есть В;
обозначение: —>, =>;
таблица истинности:
Импликация истинна всегда, за исключением случая,
когда А истинно, а В ложно,
Пример: Если идет дождь, то земля мокрая.
Слайд 10
Эквиваленция (равнозначность), от лат. Aequivalens - равноценное:
соответствует речевым
оборотам ЭКВИВАЛЕНТНО: необходимо и достаточно для; тогда и
только тогда, когда;обозначение: =, < >, <=>;
таблица истинности:
Эквиваленция истинна тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
Пример: Я пойду гулять тогда и только тогда, когда выучу все уроки.
Слайд 11
ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
ОПЕРАЦИЯ В СКОБКАХ;
ОТРИЦАНИЕ;
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ;
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ;
ИМПЛИКАЦИЯ;
ЭКВИВАЛЕНЦИЯ.
Слайд 12
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ
Построение таблиц истинности:
определить число
переменных;
определить число строк в таблице истинности;
записать
все возможные значения переменных; определить количество логических операций и их порядок;
записать логические операции в таблицу истинности и определить для каждой значение;
подчеркнуть значения переменных, для которых F = 1.