Презентация на тему по теме Декартово произведение множеств

плоскости:
на 1-ой позиции – абсцисса,
на 2-ой –

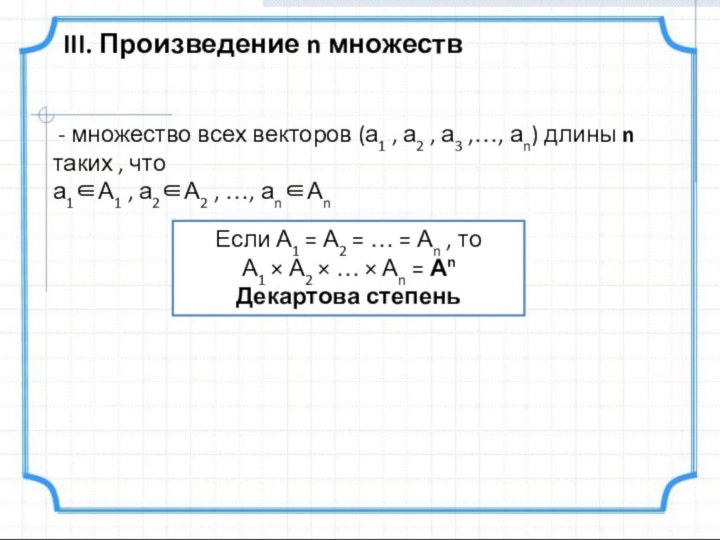
ордината

Вектор (кортеж) –
упорядоченный набор элементов
х = (х1, х2, …, хn)
где хi – координаты (компоненты)

Длина (размерность) вектора –
количество его координат

их соответствующие компоненты равны:
х = y ⇔ ∀i

xi = yi
#2.
{1, 2} = {2, 1, 1} = {2, 1}
НО (1, 2) ≠ (2, 1, 1) ≠ (2, 1)
Только (1, 2) = (1, 2)

произведение множеств A и B есть множество всех упорядоченных

пар (a, b) таких, что a∈A, b∈B.
A×B={ (a, b) | a∈A, b∈B }

#3. Найдите декартово произведение множеств
А={1, 2}, B={3, 4, 5}
А×B = { (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5) }

#4. A={1, 2, 3, 4, 5, 6, 7, 8}, B={a, b, c, d, e, f, g, h}
А×В – обозначение клеток шахматной доски

Упорядоченная пара

Если А = В
то А × В = А2
Декартов квадрат

, то
А1 × А2 × … × Аn =

Аn
Декартова степень

III. Произведение n множеств

- множество всех векторов (а1 , а2 , а3 ,…, аn) длины n таких , что
а1∈А1 , а2∈А2 , …, аn∈Аn

и y∈R,
- координаты точек плоскости

#6. Х = {1,2,3},

У= {0,1}: Х×У -? и У×Х - ?
Х×У= {(1,0), (1,1), (2,0), (2,1), (3,0), (3,1)}
У×Х= {(0,1), (0,2), (0,3), (1,1), (1,2), (1,3)}

Не обладает свойством коммутативности

2), (1; 1) и (1; 2)
#7. Прямое произведение 2

бесконечных множеств – числовых отрезков:
[0; 1]×[1; 2]

Декартово произведение.doc»

и В – конечные множества и n(А) = m1

, n(В) = m2 ⇒
n(А × В) = n(А) ⋅ n(В) = m1 ⋅ m2


Обоснование:
∀ из m1 элементов мн-ва А может составить пару с ∀ из m2 элементов мн-ва В
⇒ m1 ⋅ m2 - различных пар

Общее правило произведения:
А1 , А2 , …, Аk – конечные множества и n( А1) = m1 , n(А2) = m2 , …, n( Аk) = mk ⇒
n(А1 × А2 × … × Аk) = n( А1) ⋅ n(А2) ⋅ … ⋅ n( Аk)
Следствие: n(An) = (n(A))n

5; 6; 7; 8}, B={a; b; c; d; e;

f; g; h}. Найти n(А × В).

Решение:
n(A×B) = n(А) ⋅ n(B)
n(A×B) = 8 ⋅ 8 = 64


Ответ: 64

Дано:
n(A) = 8
n(B) = 8

Найти:
n(A×B) - ?

n(X × Y), n(Y × X).
Решение:
Х×У= {(1; 0),

(1; 1), (2; 0), (2; 1), (3; 0), (3; 1)}
У×Х= {(0; 1), (0; 2), (0; 3), (1; 1), (1; 2), (1; 3)}

n(A×B) = n(А) ⋅ n(B)

n(X×Y) = 3 ⋅ 2 = 6
n(Y×X) = 2 ⋅ 3 = 6

Ответ: n(X×Y) = n(Y×X) = 6

можно составить из цифр от 1 до 9.
Решение:
n(A×B)

= n(А) ⋅ n(B)
n(A2) = (n(А))2

n(A×А) = 9 ⋅ 9 = 81
- кол-во 2-узначных чисел из цифр от 1 до 9

Ответ: 81

Дано:
А={1;2;3;4;5;6;7;8;9}
n(A) = 9
2-узначное число – упорядоченная пара

Найти:
n(A×А) = n(A2) - ?

можно составить из цифр множества В= {5; 2; 7}.
Решение:
n(В3)

= (n(В))3

n(В3) = 33 = 27
- кол-во 3-значных чисел из цифр 5, 2, 7


Ответ: 27

Дано:
В={5; 2; 7}
n(В) = 3
3-значное число – кортеж длины 3

Найти:
n(В×В×В) = n(В3) - ?

Цифры в записи числа могут повторяться

произведения A×B×C множеств
A ={1; 4; 7}, B =

{0; 2}, C = {5}.

Решение:
1) Длина каждого вектора: 3
2) Количество векторов:
n(A×B×C) = n(A) ⋅ n(B) ⋅ n(C) = 3⋅2⋅1 = 6

Проверка:
A×B×C = {(1;0;5), (1;2;5), (4;0;5), (4;2;5), (7;0;5), (7;2;5)}

фигуры (окружность, квадрат, треугольник или шестиугольник), буквы (русского алфавита)

и цифры. Сколько различных знаков может нарисовать Серёжа?

А1

Ю9

Дано:
А – фигуры
В – буквы
С – цифры
n(А) = 4
n(В) = 33
n(С) = 10
1 знак – кортеж длины 3
Найти:
n(А×В×С) - ?

Решение:
n(A×B×С) = n(А)⋅n(B)⋅n(С)

n(А×В×С) = 4⋅33⋅10 = 1320
- различных знаков





Ответ: 1320