Ваня, играют в следующую игру. Перед игроками лежат две
кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.





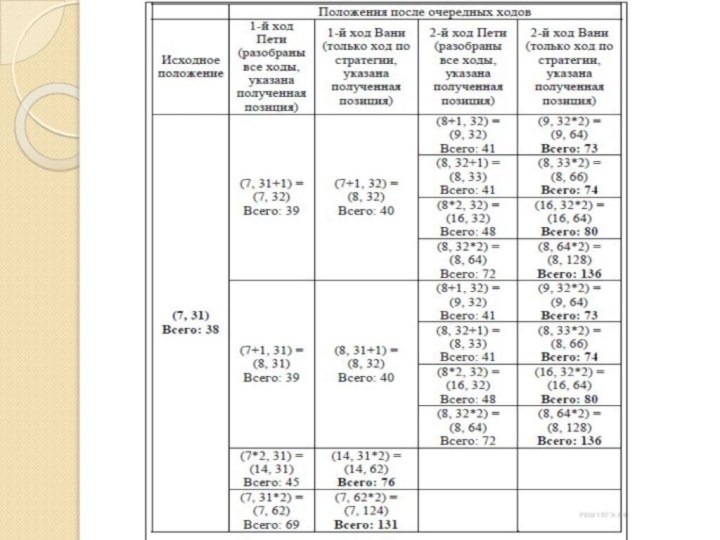








![Презентация к семинару методического объединения учителей информатики г.Арзамас Полное решение:var a: array[1..1440] of byte; i, j, N, max, s: integer; begin](/img/tmb/7/662832/fb7e4c7ade831874cf6cabdd3ce0a15f-720x.jpg)


![Презентация к семинару методического объединения учителей информатики г.Арзамас Полное решение:var a: array[1..5] of integer; s, i, j, max, N: integer; begin readln(n);](/img/tmb/7/662832/2ebfdbff6e9470a0ee1bb9f0795e6674-720x.jpg)