Слайд 4
Формирование изображения камерой
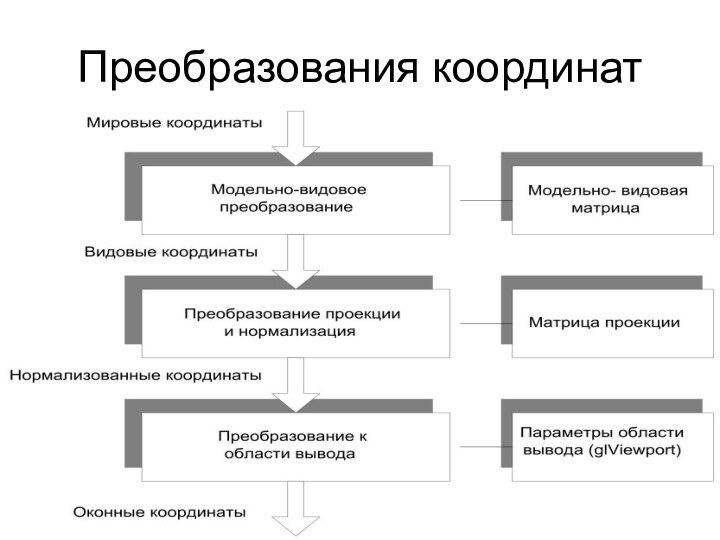
Установить штатив и направить камеру на
сцену (видовое преобразование).
Подготовить сцену в нужной композиции (модельное преобразование).
Подобрать
объектив или отрегулировать масштабирование (преобразование проекции).
Определить размер изображения (преобразование в порт просмотра).
Слайд 5
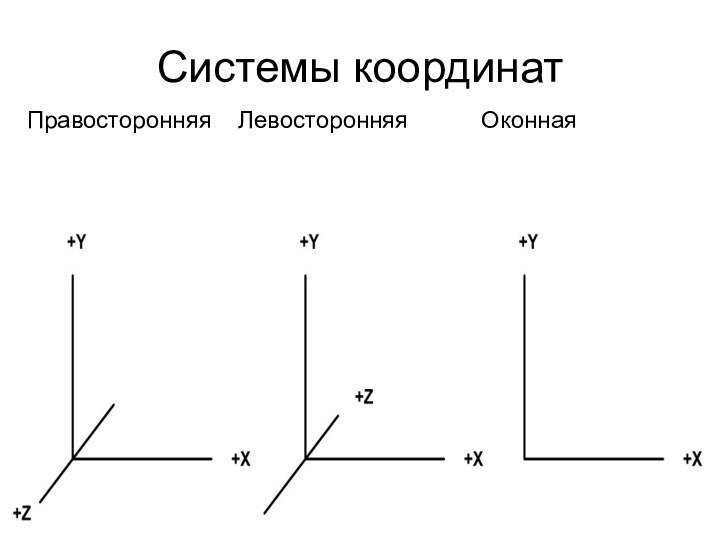
Системы координат OpenGL
Правосторонняя: модельно-видовые преобразования.
Левосторонняя: установка параметров проецирования.
Оконная:
преобразование в порт просмотра.
Слайд 7
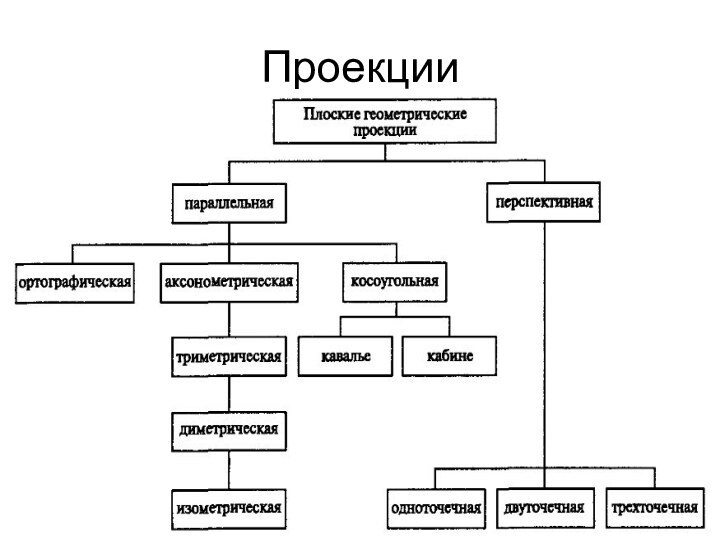
Плоские геометрические проекции объектов
Плоские геометрические проекции объектов образуются
пересечением прямых, называемых проекторами, с плоскостью, называемой центром проекции.
Проекторы
– это прямые, проходящие через произвольную точку, называемую центром проекции, и каждую точку объекта.
Слайд 8
Перспективные и параллельные проекции
Перспективная проекция: центр проекции расположен
в конечной точке трехмерного пространства.
Параллельная проекция: центр проекции расположен
в бесконечности (проекторы параллельны).
Слайд 9
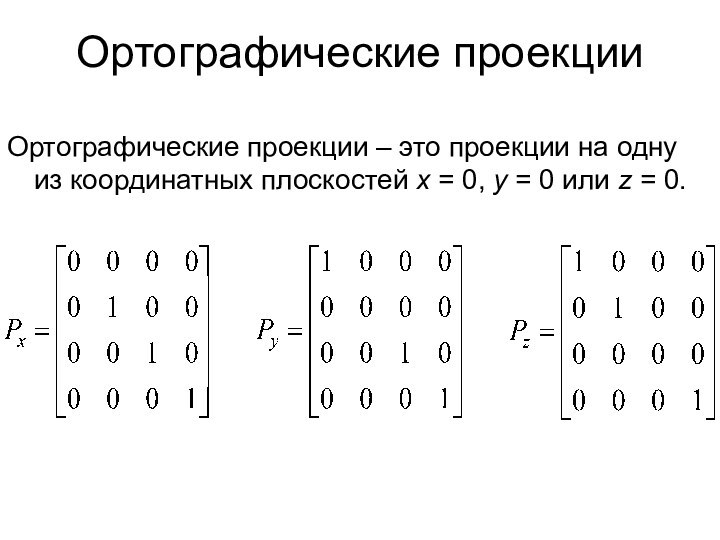
Ортографические проекции
Ортографические проекции – это проекции на одну
из координатных плоскостей x = 0, y = 0
или z = 0.
Слайд 10
Аксонометрические проекции
Аксонометрические проекции – это проекции на плоскость,
не являющуюся одной из координатных плоскостей x = 0,
y = 0 или z = 0.
Триметрическая проекция строится произвольными поворотами вокруг произвольных координатных осей в произвольном порядке с последующим проецированием на плоскость z = 0.
Диметрическая проекция – это триметрическая проекция с двумя одинаковыми коэффициентами искажения и произвольным третьим коэффициентом.
Изометрическая проекция – это триметрическая проекция, в которой все три коэффициента искажения равны
Слайд 14
Косоугольные проекции
Косоугольная проекция – это проекция, которая формируется
параллельными проекторами, расположенными под косым углом к плоскости проекции.
Проекция
кавалье получается когда угол между проекторами и плоскостью проекции составляет 45°.
Проекция кабине получается когда угол между проекторами и плоскостью проекции составляет arctg(1/2).
Слайд 16
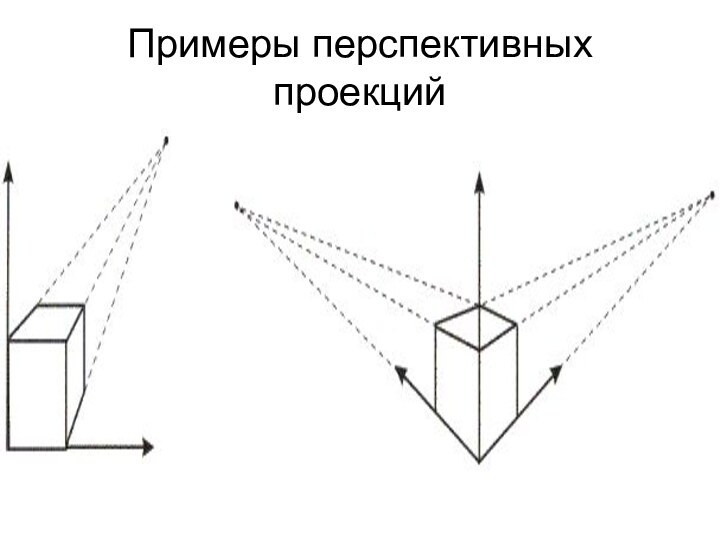
Перспективные проекции
Перспективная проекция получается в результате перспективного преобразования.
При
перспективном преобразовании параллельные прямые сходятся, размер объекта уменьшается с
увеличением расстояния до центра проекции и происходит неоднородное искажение линий объекта, зависящее от ориентации и расстояния от объекта до центра проекции.
Перспективная проекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Перспективные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, т.е. от числа координатных осей, которые пересекают проекционную плоскость.
Слайд 18
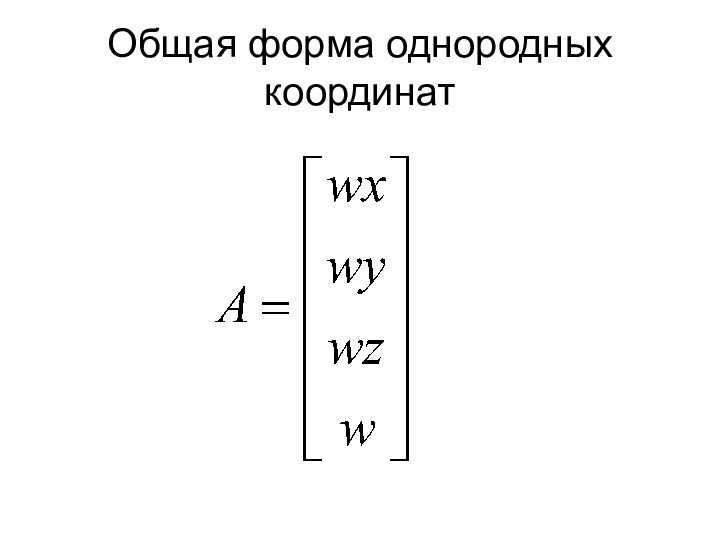
Общая форма однородных координат
Слайд 19
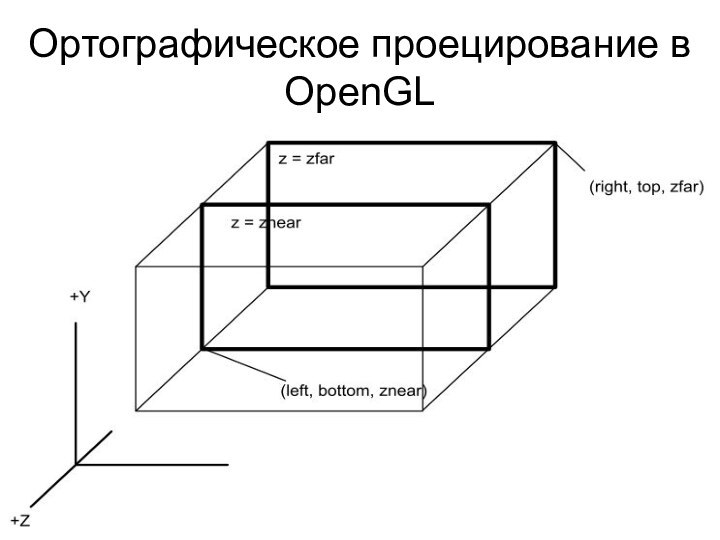
Ортографическое проецирование в OpenGL
Слайд 20
Функции ортографического преобразования
void glOrtho(GLdouble l, GLdouble r, GLdouble
b, GLdouble t, GLdouble n, GLdouble f);
void gluOrtho2D(GLdouble l,
GLdouble r, GLdouble b, GLdouble t);
// glOrtho(l, r, b, t, –1.0, 1.0);
Слайд 21
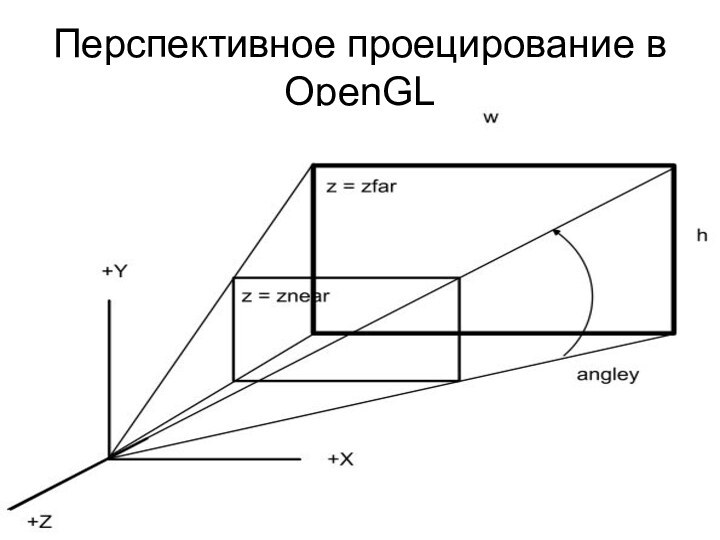
Перспективное проецирование в OpenGL
Слайд 22
Матрица перспективного проецирования
Слайд 23
Функции перспективного преобразования
void glFrustum(GLdouble l, GLdouble r, GLdouble
b, GLdouble t, GLdouble n, GLdouble f);
void gluPerspective(GLdouble angle,
GLdouble aspect, GLdouble n, GLdouble f);
t = n * tg(π / 180 * angle / 2);
b = –t;
r = t * aspect;
l = –r;
Слайд 24
Пример программы
…
void setShape(float vAng, float asp, float nearD,
float farD)
{
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(vAng, asp, nearD, farD);
}
…
setShape(30.0f, 64.0f/48.0f, 0.5f, 50.0f);
…