целые n и m — соответственно число вершин и
число рёбер неориентированного графа (1 ≤ n ≤ 10 000, 0 ≤ m ≤ 50 000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами.В файл output.txt вывести единственное число — количество компонент связности графа.
Ограничение по времени — 1 сек.
Ограничение по памяти — 16 Мб.



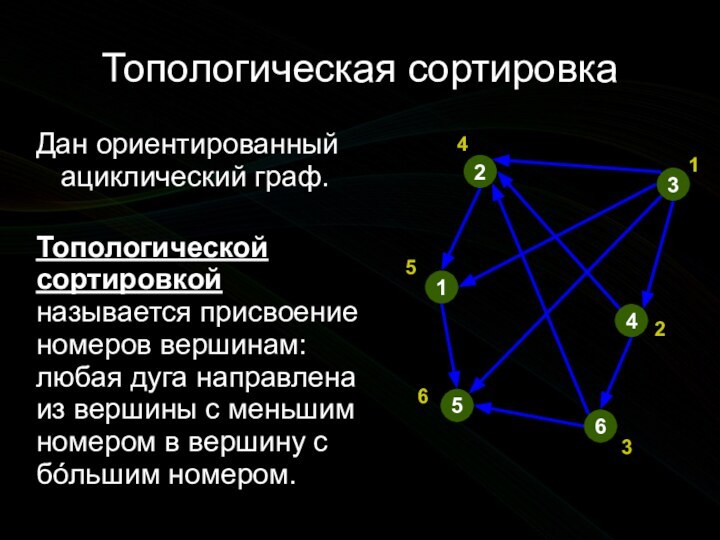
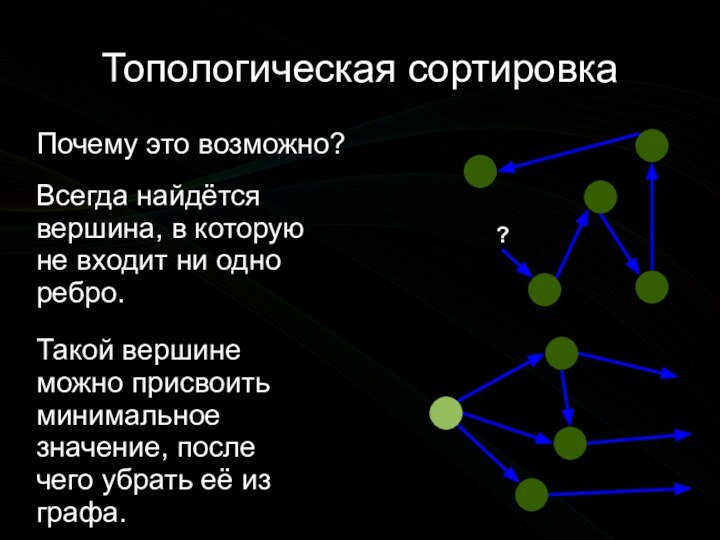

![Алгоритмы на графах. Топологическая сортировка отсечением вершин Топологическая сортировкамассив order длины n, order[i] — присвоенный i-й вершине порядковый номер](/img/tmb/11/1076121/4a5db63809a79e3096d5f3bbd96c76e0-720x.jpg)



































