- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алогритм Дейкстры
Содержание
- 2. Алгоритм Дейкстры — алгоритм на графах, изобретённый
- 3. ПРИМЕР 1Необходимо найти все кратчайшие пути от вершины №1 для графа, представленного на рисунке:
- 4. СОСТАВИМ МАТРИЦУ ДЛИН КРАТЧАЙШИХ ДУГ ДЛЯ ДАННОГО
- 5. НАХОДИМ БЛИЖАЙШУЮ ВЕРШИНУ К ОКРАШЕННОЙ НАМИ,
- 6. Минимальную длину имеет путь от вершины 1
- 7. Минимальную длину имеет путь от вершины 1
- 8. ОРИЕНТИРОВАННОЕ ДЕРЕВО С КОРНЕМ В ВЕРШИНЕ №1
- 9. ПРИМЕР 2Рассмотрим выполнение алгоритма на примере графа,
- 10. Кружками обозначены вершины, линиями — пути между
- 11. ПЕРВЫЙ ШАГРассмотрим шаг алгоритма Дейкстры для нашего
- 12. Первый по очереди сосед вершины 1 —
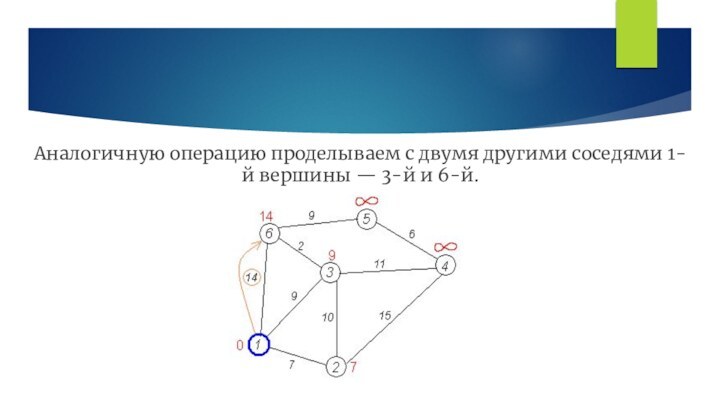
- 13. Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
- 14. Все соседи вершины 1 проверены. Текущее минимальное
- 15. ВТОРОЙ ШАГШаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
- 16. Снова пытаемся уменьшить метки соседей выбранной вершины,
- 17. Ещё один сосед вершины 2 — вершина
- 18. Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
- 19. ТРЕТИЙ ШАГПовторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
- 20. Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся
- 21. ПРИМЕР 3Найдите кратчайший путь от Москвы до Королёва.
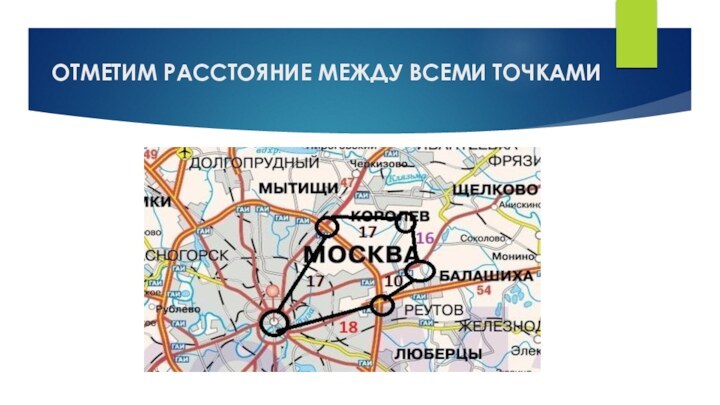
- 22. ОТМЕТИМ РАССТОЯНИЕ МЕЖДУ ВСЕМИ ТОЧКАМИ
- 23. РАССЧИТАЕМ НАИКРАТЧАЙШИЙ ПУТЬ ДО КОРОЛЕВАИсходя из того,
- 24. ОБОЗНАЧЕНИЯV — множество вершин графаE — множество
- 25. ПСЕВДОКОДПрисвоим d[a] ← 0, p[a] ← aДля
- 26. ОПИСАНИЕВ простейшей реализации для хранения чисел d[i]
- 27. Скачать презентацию
- 28. Похожие презентации
Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко











![Алогритм Дейкстры ОБОЗНАЧЕНИЯV — множество вершин графаE — множество ребер графаw[ij] — вес (длина)](/img/tmb/15/1459116/924c06eeb3c5501ce57312df465e8597-720x.jpg)
![Алогритм Дейкстры ПСЕВДОКОДПрисвоим d[a] ← 0, p[a] ← aДля всех x V отличных от](/img/tmb/15/1459116/66dfbad4244b1c86ea5fa1be42c16f92-720x.jpg)
![Алогритм Дейкстры ОПИСАНИЕВ простейшей реализации для хранения чисел d[i] можно использовать массив чисел, а](/img/tmb/15/1459116/caa3684422bd650fc055b7b096e33f9e-720x.jpg)

Слайд 3
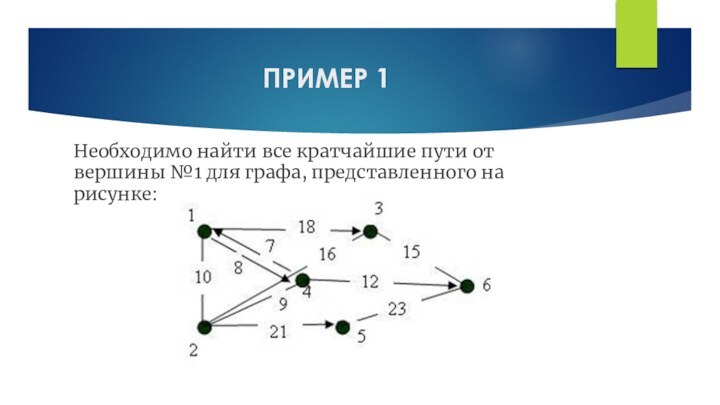
ПРИМЕР 1
Необходимо найти все кратчайшие пути от вершины
№1 для графа, представленного на рисунке:
Слайд 4
СОСТАВИМ МАТРИЦУ ДЛИН КРАТЧАЙШИХ ДУГ ДЛЯ ДАННОГО ГРАФА
Cтартовая
вершина, от которой строится дерево кратчайших путей - вершина
1. Задаем стартовые условия:d(1)=0, d(x)=∞
Окрашиваем вершину 1, y=1.
Слайд 5
НАХОДИМ БЛИЖАЙШУЮ ВЕРШИНУ К ОКРАШЕННОЙ НАМИ, ИСПОЬЗУЯ ФОРМУЛУ
d(x)=min{d(x);
d(y)+ ay,x}
d(2)=min{d(2);d(1)+a(1,2)}=min{∞;0+10}=10
d(3)=min{d(3);d(1)+a(1,3)}=min{∞;0+18}=18
d(4)=min{d(4);d(1)+a(1,4)}=min{∞;0+8}=8
d(5)=min{d(5);d(1)+a(1,5)}=min{∞;0+∞}=∞
d(6)=min{d(6) ; d(1)+a(1,6)}=min{∞; 0+∞}=∞
Слайд 6 Минимальную длину имеет путь от вершины 1 до
вершины 4 d(4)=8. Включаем вершину №4 в текущее ориентированноe
дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,4)d(2)=min{d(2);d(4)+a(4,2)}=min{10;8+9}=10 d(3)=min{d(3);d(4)+a(4,3)}=min{18;8+∞}=18 d(5)=min{d(5);d(4)+a(4,5)}=min{∞;8+∞}=∞ d(6)=min{d(6) ; d(4)+a(4,6)}=min{∞; 8+12}=20
Минимальную длину имеет путь от вершины 1 до вершины 2 d(2)=10. Включаем вершину №2 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,2) d(3)=min{d(3);d(2)+a(2,3)}=min{18;10+16}=18 d(5)=min{d(5);d(2)+a(2,5)}=min{∞;10+21}=31 d(6)=min{d(6) ; d(2)+a(2,6)}=min{20; 10+∞}=20
Слайд 7 Минимальную длину имеет путь от вершины 1 до
вершины 3 d(3)=18. Включаем вершину №3 в текущее ориентированноe
дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,3) d(5)=min{d(5);d(3)+a(3,5)}=min{31;18+15}=31 d(6)=min{d(6) ; d(3)+a(3,6)}=min{20; 18+∞}=20Минимальную длину имеет путь от вершины 1 до вершины 6 d(6)=20. Включаем вершину №6 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (4,6) d(5)=min{d(5) ; d(6)+a(6,5)}=min{31; 20+23}=31
Минимальную длину имеет путь от вершины 1 до вершины 5 d(5)=31. Включаем вершину №5 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (2,5)
Слайд 9
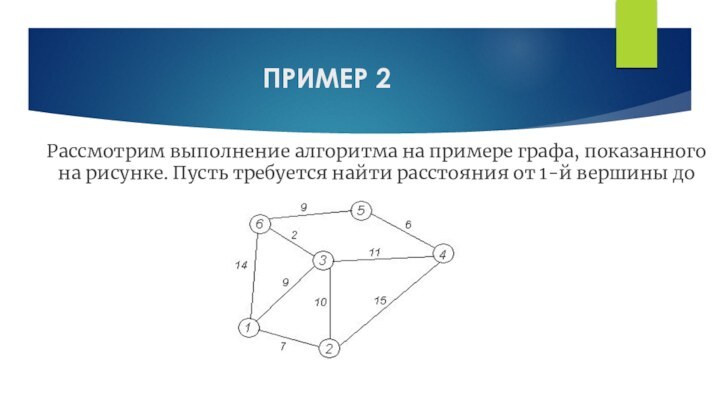
ПРИМЕР 2
Рассмотрим выполнение алгоритма на примере графа, показанного
на рисунке. Пусть требуется найти расстояния от 1-й вершины
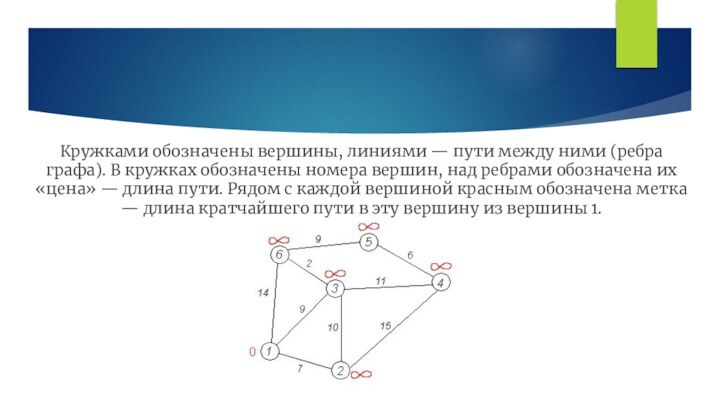
до всех остальных.Слайд 10 Кружками обозначены вершины, линиями — пути между ними
(ребра графа). В кружках обозначены номера вершин, над ребрами
обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Слайд 11
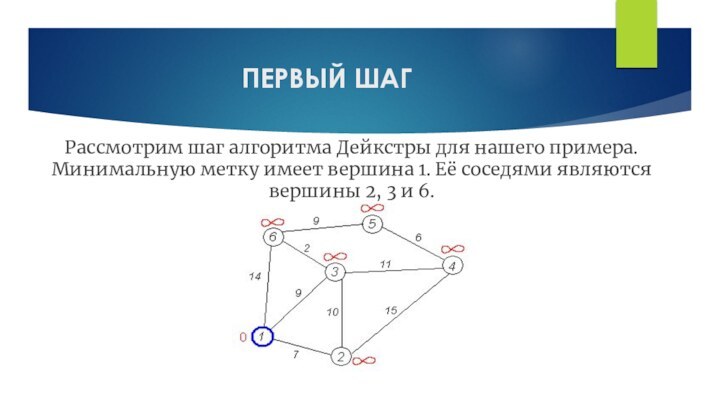
ПЕРВЫЙ ШАГ
Рассмотрим шаг алгоритма Дейкстры для нашего примера.
Минимальную метку имеет вершина 1. Её соседями являются вершины
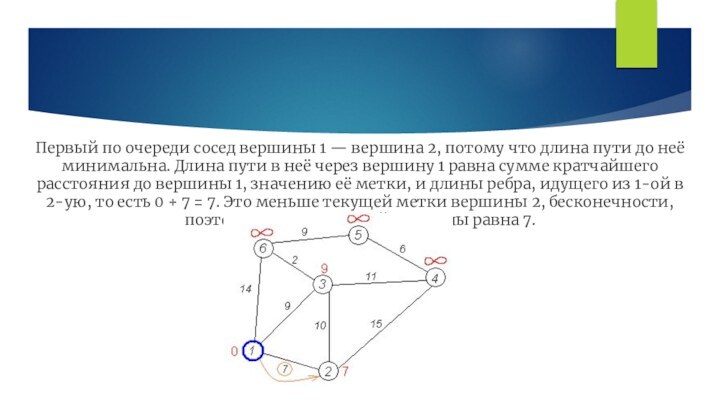
2, 3 и 6.Слайд 12 Первый по очереди сосед вершины 1 — вершина
2, потому что длина пути до неё минимальна. Длина
пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-ой в 2-ую, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.Слайд 14 Все соседи вершины 1 проверены. Текущее минимальное расстояние
до вершины 1 считается окончательным и пересмотру не подлежит
(то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Слайд 15
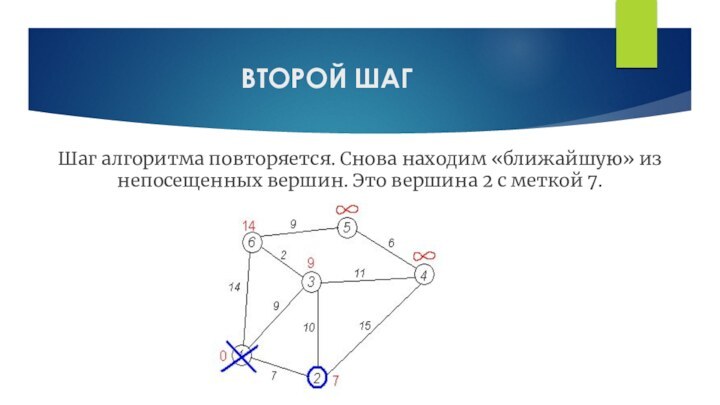
ВТОРОЙ ШАГ
Шаг алгоритма повторяется. Снова находим «ближайшую» из
непосещенных вершин. Это вершина 2 с меткой 7.
Слайд 16 Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь
пройти в них через 2-ю вершину. Соседями вершины 2
являются вершины 1, 3 и 4.Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
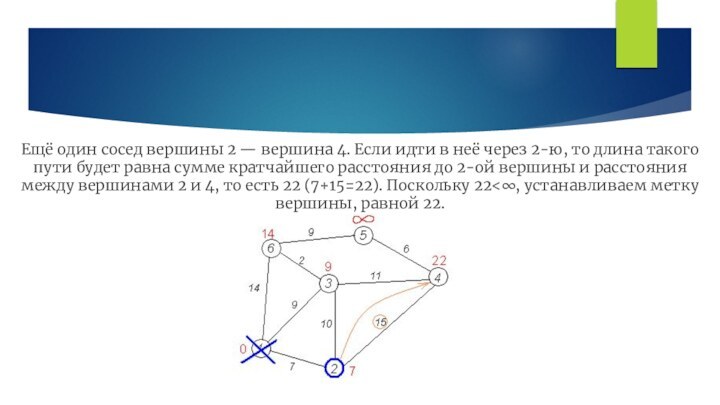
Слайд 17 Ещё один сосед вершины 2 — вершина 4.
Если идти в неё через 2-ю, то длина такого
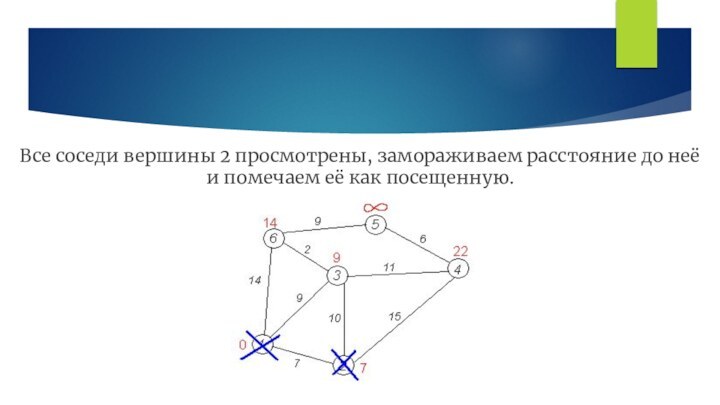
пути будет равна сумме кратчайшего расстояния до 2-ой вершины и расстояния между вершинами 2 и 4, то есть 22 (7+15=22). Поскольку 22<∞, устанавливаем метку вершины, равной 22.Слайд 18 Все соседи вершины 2 просмотрены, замораживаем расстояние до
неё и помечаем её как посещенную.
Слайд 19
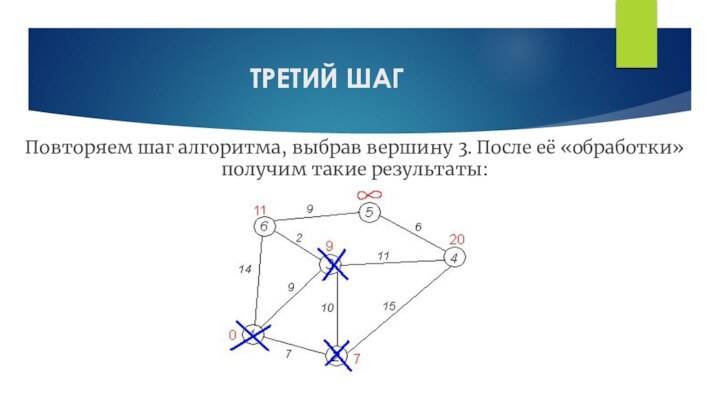
ТРЕТИЙ ШАГ
Повторяем шаг алгоритма, выбрав вершину 3. После
её «обработки» получим такие результаты:
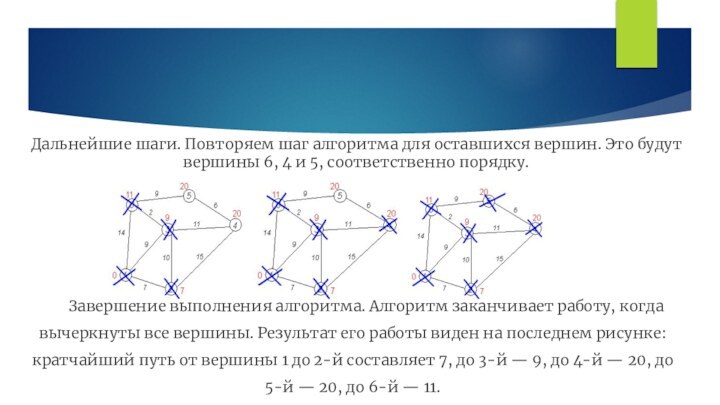
Слайд 20 Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин.
Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение
выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Слайд 23
РАССЧИТАЕМ НАИКРАТЧАЙШИЙ ПУТЬ ДО КОРОЛЕВА
Исходя из того, что
совокупное расстояние от А до D (включая B и
С) равно 44, а расстояние от А до D (включая Е) равно 34, делаем вывод, что наикратчайший путь от Москвы до Королева – путь через точки А, Е, D.
Слайд 24
ОБОЗНАЧЕНИЯ
V — множество вершин графа
E — множество ребер
графа
w[ij] — вес (длина) ребра ij
a — вершина, расстояния
от которой ищутсяU — множество посещенных вершин
d[u] — по окончании работы алгоритма равно длине кратчайшего пути из a до вершины u
p[u] — по окончании работы алгоритма содержит кратчайший путь из a в u
Слайд 25
ПСЕВДОКОД
Присвоим d[a] ← 0, p[a] ← a
Для всех
x V отличных от a;
Присвоим d[u] ← ∞
Пока ∃v
∉ UПусть v ∉ U — вершина с минимальным d[v]
Для всех u ∉ U таких, что vu∈ E
Если d[u]>d[v]+w[vu], то
Изменим d[u] ← d[v]+w[vu]
Изменим p[u] ← p[v], u
Слайд 26
ОПИСАНИЕ
В простейшей реализации для хранения чисел d[i] можно
использовать массив чисел, а для хранения принадлежности элемента множеству
U — массив булевых переменных.В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (бо́льшим максимального возможного пути в графе). Массив флагов заполняется нулями. Затем запускается основной цикл.
На каждом шаге цикла мы ищем вершину с минимальным расстоянием и флагом равным нулю. Затем мы устанавливаем в ней флаг в 1 и проверяем все соседние с ней вершины. Если в ней расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то уменьшаем его. Цикл завершается когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0 d[i] = ∞. Последний случай возможен тогда и только тогда, когда граф G не связан.