Презентация на тему Аттестационная работа. Компьютерное моделирование и проектная и исследовательская деятельность учащихся

по проведению практикума на уроках информатики (компьютерного моделирования), имеющая

элементы исследовательской работы и порождающей другие аналогичные исследовательские работы.

№26» г. Подольска.
Окончил в 1973 году мехмат МГУ им.

М.В.Ломоносова, долгие годы работал в НИИ, а в 1976 по призыву партии и правительства пришел в школу преподавать тогда еще новый предмет – информатику, был первым учителем информатики города Подольска, сначала по совместительству, ну а с развалом СССР (и следом моего НИИ) в школе на постоянной работе. В течение 15 лет руководил городским методическим объединением учителей информатики.

опыт, последние годы почувствовал, что отстаю от молодых коллег

именно в части организации научно-исследовательской и проектной работы, что и привело меня на Ваши курсы.

работаю, - одно из лучших учебных заведений города, последние

годы регулярно входит в Топ лучших школ области, а недавно получил областной Грант за работу с одаренными детьми, т.е. за достижения учащихся на олимпиадах, конкурсах и конференциях а разного уровня.

лицея, который я веду, можно найти списки учащихся, ставших

призерами различных конкурсов научно-исследовательских и проектных работ (последний учебный год – более100), посмотреть страницу научного общества «Эйнштейн», через сайт познакомиться с творческими работами учащихся.

классов старшей школы, в том числе физико-математический и информационно-технологический,

в которых информатика изучается на углубленном уровне.
В ИТ классе, помимо уроков информатики, есть элективный курс «Компьютерное моделирование», автором программы которого я и являюсь.
Этот курс направлен на организацию проектной и исследовательской деятельности учащихся.

курса «Компьютерного моделирования».
Разработка родилась из п. 23 учебника

И.Г.Семакина для 9 класса. Там представлена математическая модель «Рыбы в пруду», основанная на законе Мальтуса и предназначенная для реализации в электронных таблицах.
Несколько слайдов из презентации к уроку размещено в Приложении 1.
Но сама эта несложная в реализации модель дает возможность стимулировать учащихся к ее развитию и совершенствованию.

предложенной модели.
2-ый этап работы – исследование популяции с помощью

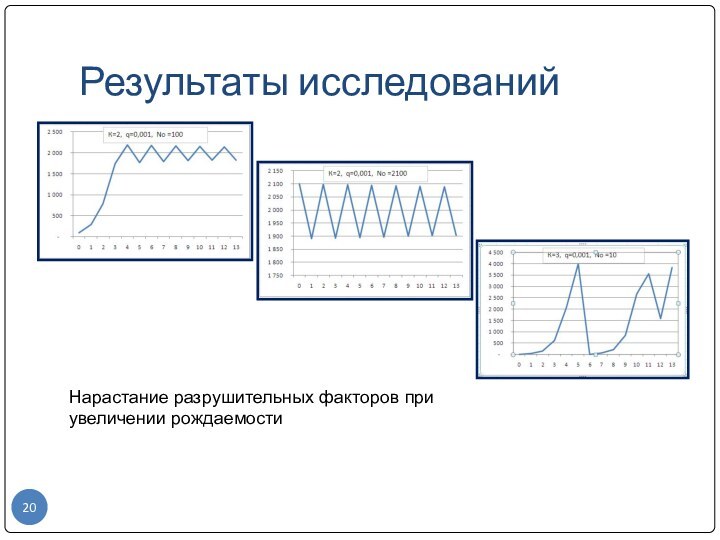
модели в зависимости от значений исходных коэффициентов. Оно проводится по единому для всех учащихся заданию
Это исследование должно привести учащихся к обнаружению такого явления как неустойчивость экологической системы (сначала - колебательное поведение затем пилообразное и далее система «идет в разнос», т.е.разрушение системы).

ли в действительности?»
Возникает необходимость изучения адекватности модели (а для

этого есть книги и Интернет).
Возникают идеи – а как развить модель.
Один из предложенных вариантов развития – ввести в модель отлов рыбы и исследовать влияние отлова на устойчивость системы (скоро выясняется, что умеренный отлов повышает устойчивость),
Появляется проблема, а каков максимальный отлов, например, за 10 лет, не разрушающий экологическую устойчивость и вопрос, как технически с помощью электронных таблиц или же программирования его найти.

иными более сложными экологическими моделями, узнать их истоки, их

значение в науке, научиться методам компьютерной реализации (это экологические модели Вольтерра и им подобные).
Появляется несколько вариантов индивидуальных и групповых работ. Это модели:
«зайцы-трава»,
«хищник-жертва»,
«конкурирующие виды».

компьютерную модель, но и исследовать поведение исследуемого объекта (экологической

системы) в зависимости от тех или иных параметров), найти подтверждение качественной адекватности модели реальной действительности.
Выполнение этих задач и является критерием оценки труда учащихся.

внедрению проектной и исследовательской деятельности в учебный процесс.
Кроме экологических

моделей, естественно, рассматриваются и физические, как широко известные («Движение тела, брошенного под углом к горизонту», «Посадка на Луну» и т.п.), так и реализующие замысел учащихся (например, движение нескольких заряженных тел в электромагнитном поле).
Компьютерная модель становится инструментом для исследования поведения того или иного объекта.

выдающего советского математика В. И. Арнольда:
«Умение думать важнее

умения нажимать на кнопки компьютера»
С появлением ЕГЭ все сложнее и сложнее найти время воспитания такого умения, но это крайне необходимо.

установили, что прирост какого-либо вида живых организмов за счет

рождаемости прямо пропорционален его количеству,
а убыль за счет смертности прямо пропорциональна квадрату его коли-чества.
Этот закон известен как закон Мальтуса.

решили провести расчеты.
Согласно закону Мальтуса, изменение числа рыб за

год вычисляется по формуле:

ΔN =k·N-q·N2,
где N – число карпов в начале года,
k – коэффициент прироста,
q – коэффициент смертности.

и в данных условиях k=1, q=0,001.
От каких

факторов зависят значения этих коэффициентов?

через год их будет
N1 = N0 +k·N0 - q·N02
Через

два года:
N2 = N1 +k·N1 - q·N12
и т.д.
Получается общая формула для i-го года:
Ni = Ni-1 +k·Ni-1 - q·Ni-12

Эта формула и будет математической моделью процесса размножения рыб в водоёме.

же с помощью программирования).
Создать визуализацию модели (график, диаграмма или

что-то иное).
Исследовать поведение объекта при различных исходных данных, выявить и проинтерпретировать закономерности.
Подумать над возможным развитием модели, внесением в нее каких-либо новых факторов.