- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Деревья оптимального поиска (ДОП)
Содержание
- 2. Типичный пример - сканер компилятора, который определяет,
- 3.
- 4.
- 5. 103060103060103060103060103060
- 6.
- 7. Задача построения ДОП может ставиться в двух
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17. (0,9)(5,9)(0,4)(1,4)(1,3)(2,3)(0,0)(1,1)(2,2)(3,3)(4,4)(9,9)(8,8)(7,7)(6,6)(5,5)(5,8)(5,6)(7,8)
- 18.
- 20. Алгоритм построения ДОП
- 21. Алгоритм построения ДОППри h>1:
- 22.
- 24. Приближенные алгоритмы построения ДОПИзвестны быстрые алгоритмы, строящие
- 25. 252051010105555
- 26.
- 27.
- 28.
- 29.
- 30.
- 31. К У Р А П О В
- 32. Скачать презентацию
- 33. Похожие презентации
Типичный пример - сканер компилятора, который определяет, относится ли каждое слово программы (идентификатор) к классу ключевых слов.Статистические измерения на сотнях компилируемых программ могут дать информацию об относительных частотах появления в тексте программы конкретных ключевых слов.




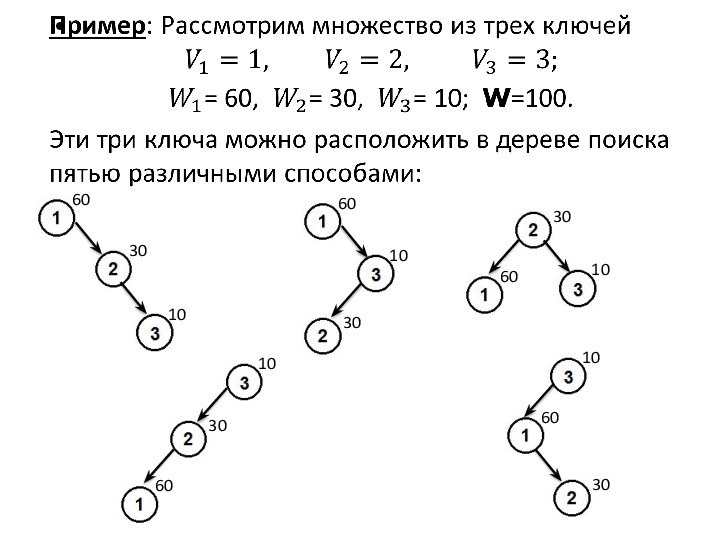










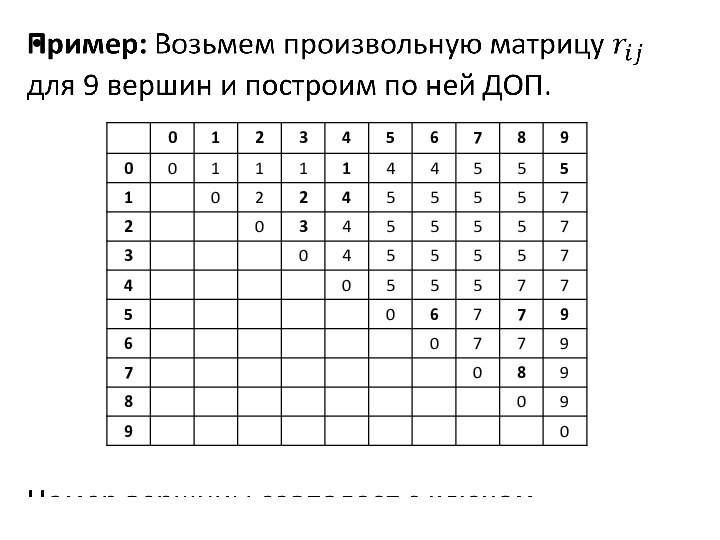
















Слайд 2 Типичный пример - сканер компилятора, который определяет, относится
ли каждое слово программы (идентификатор) к классу ключевых слов.
измерения на сотнях компилируемых программ могут дать информацию об относительных частотах появления в тексте программы конкретных ключевых слов.
Слайд 7
Задача построения ДОП
может ставиться в двух вариантах:
Известны
вершины и их веса (дерево не меняется в процессе
поиска).Вес вершины определяется в процессе работы (после каждого поиска вершины её вес увеличивается на единицу).
В этом случае нужно перестраивать структуру дерева.
Слайд 17
(0,9)
(5,9)
(0,4)
(1,4)
(1,3)
(2,3)
(0,0)
(1,1)
(2,2)
(3,3)
(4,4)
(9,9)
(8,8)
(7,7)
(6,6)
(5,5)
(5,8)
(5,6)
(7,8)
Слайд 21
Алгоритм построения ДОП
При h>1:
h = j–i – размер
поддереваDO ( h = 2, 3, …, n )
DO ( i = 0, ..., n – h )
j := i + h
m := AR i, j-1
min : = AP i, m-1 + AP m, j
DO ( k = m+1, ..., AR i+1, j )
x : = AP i, k-1 + AP k, j
IF ( x < min ) m := k , min := x FI
OD
AP i, j := min + AW i, j
AR i, j := m
OD
OD
Слайд 24
Приближенные алгоритмы построения ДОП
Известны быстрые алгоритмы, строящие почти
оптимальные деревья поиска. Назовем эти алгоритмы А1 и А2.
Алгоритм
А1:В качестве корня берем вершину с наибольшим весом, будем поступать так же для каждого поддерева.





























