Презентация на тему Деревья. Терминология

Содержание

2. Структура дереваКорневым деревом называется множество элементов, в
3. ОпределенияФормальное определение дерева:Один узел является деревом Этот
4. ОпределенияРодитель узла n – узел дерева, находящийся
5. ОпределенияПутем из узла n1 в узел nk
6. Определения
7. ОпределенияВысота узла n – длина самого длинного
8. Способы отображения деревьев: Вложенные множества A B C D
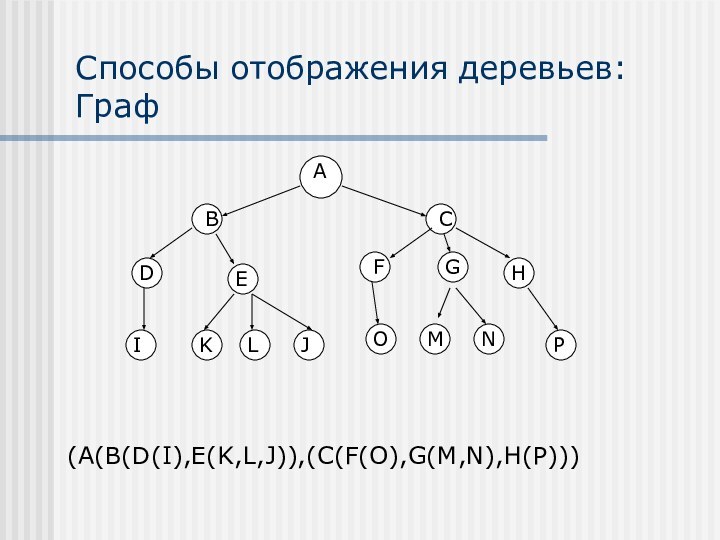
9. Способы отображения деревьев: Граф(A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))ABCFGHOMNPDEIKLJ
10. Бинарные деревьяБинарным деревом называется множество узлов, которое
11. Скачать презентацию
12. Похожие презентации

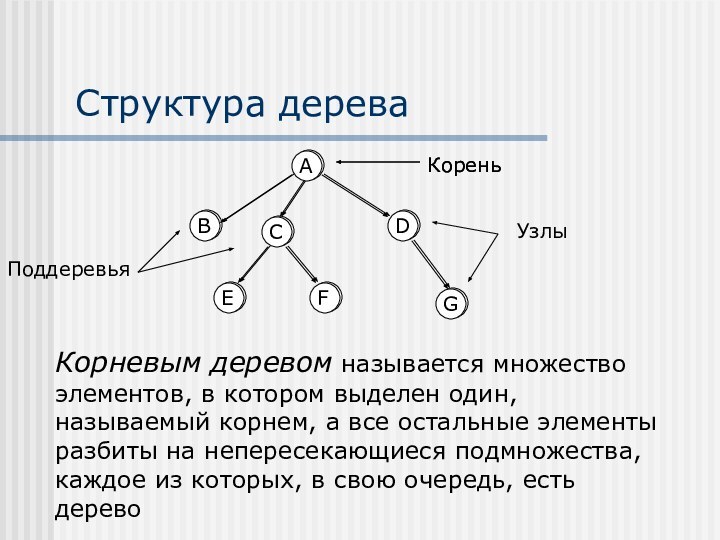
Структура дереваКорневым деревом называется множество элементов, в котором выделен один, называемый корнем, а все остальные элементы разбиты на непересекающиеся подмножества, каждое из которых, в свою очередь, есть дерево

ОпределенияФормальное определение дерева:Один узел является деревом Этот же узел является и корнем

ОпределенияРодитель узла n – узел дерева, находящийся непосредственно над узлом nДочерний узел

ОпределенияПутем из узла n1 в узел nk называется последовательность узлов n1, n2,

ОпределенияВысота узла n – длина самого длинного пути из узла n до

Способы отображения деревьев: Вложенные множества A B C D K

Способы отображения деревьев: Граф(A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))ABCFGHOMNPDEIKLJ

Бинарные деревьяБинарным деревом называется множество узлов, которое либо пусто либо разделено на

Бинарное дерево поискаУпорядоченным называется дерево, у которого непосредственные потомки каждого узла упорядочены

Слайды презентации

Слайд 2 Структура дерева
Корневым деревом называется множество элементов, в котором

Структура дереваКорневым деревом называется множество элементов, в котором выделен один, называемый

выделен один, называемый корнем, а все остальные элементы разбиты

на непересекающиеся подмножества, каждое из которых, в свою очередь, есть дерево

Слайд 3 Определения
Формальное определение дерева:
Один узел является деревом Этот же узел

ОпределенияФормальное определение дерева:Один узел является деревом Этот же узел является и

является и корнем этого дерева
Пусть n –узел, а T1

,T2 ,… ,Tk - деревья с корнями n1, n2,…, nk соответственно. Тогда можно построить новое дерево, сделав n родителем узлов n1, n2,…, nk . В этом дереве n – корень, T1 ,T2 ,… ,Tk - поддеревья, n1, n2,…, nk – сыновья узла n/

Слайд 4 Определения
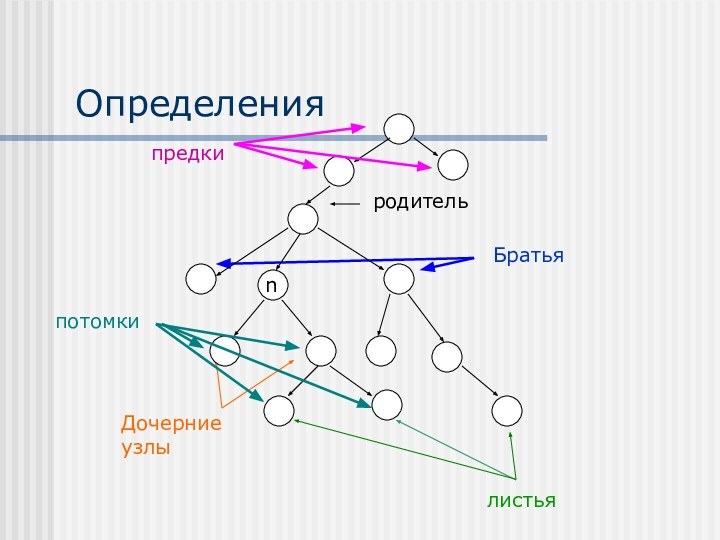
Родитель узла n – узел дерева, находящийся непосредственно

ОпределенияРодитель узла n – узел дерева, находящийся непосредственно над узлом nДочерний

над узлом n
Дочерний узел узла n –узел дерева, находящийся

непосредственно под узлом n
Корень –единственный узел дерева, не имеющий родителей
Лист – узел, не имеющий дочерних узлов
Братья – узлы, имеющие общих родителей

Слайд 5 Определения
Путем из узла n1 в узел nk называется

ОпределенияПутем из узла n1 в узел nk называется последовательность узлов n1,

последовательность узлов n1, n2, … nk , где для

всех i: 1<=IПредок узла n – узел, расположенный на пути от корня к узлу n
Потомок узла n – расположенный на пути от узла n к листу

Слайд 6 Определения

Слайд 7 Определения
Высота узла n – длина самого длинного пути

ОпределенияВысота узла n – длина самого длинного пути из узла n

из узла n до какого-нибудь листа
Высота дерева –

высота его корня
Глубина узла n – длина пути от корня до этого узла
Степень узла n – число непосредственных потомков

Слайд 8 Способы отображения деревьев: Вложенные множества
A
B C
D K

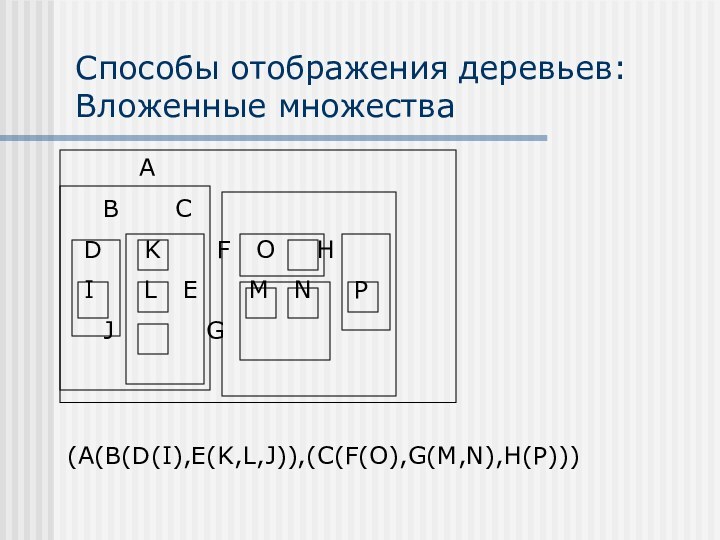
Способы отображения деревьев: Вложенные множества A B C D K F

F O H

I L E M N P
J G

(A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))

Слайд 9 Способы отображения деревьев: Граф
(A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))

A
B
C
F
G
H
O
M
N
P
D
E
I
K
L
J

Слайд 10 Бинарные деревья
Бинарным деревом называется множество узлов, которое либо

Бинарные деревьяБинарным деревом называется множество узлов, которое либо пусто либо разделено

пусто либо разделено на корень и два подмножества, которые

также представляют собой бинарные деревья
В бинарном дереве каждый узел
Либо пуст
Либо не имеет сыновей
Либо имеет только левого сына
Либо имеет только правого сына
Либо имеет двух сыновей