Презентация на тему Динамическое программирование

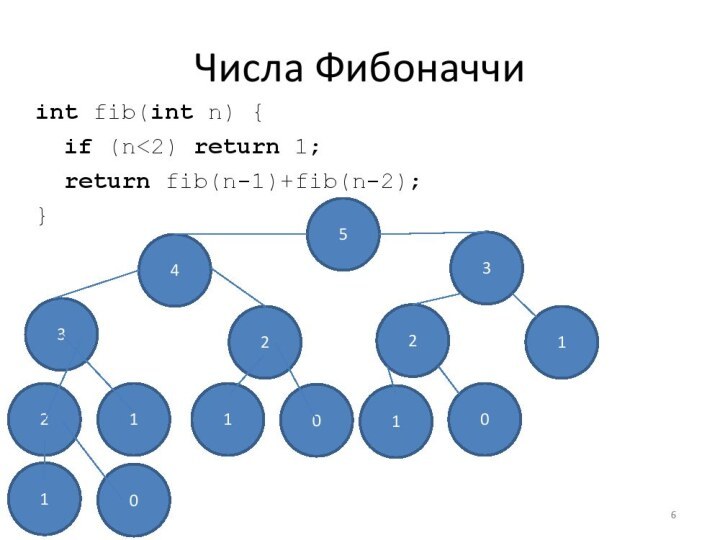
числа в массиве.
Тогда N-е число Фибоначчи легко можно найти

по следующей формуле:
F[N] = F[N-1] + F[N-2], при N > 2.

количество F всех n – битных двоичных чисел, у

которых в двоичной записи нет подряд идущих двух единиц. (N≤30).

2.
Задача об n – битных двоичных числах

ступенек, находится зайчик, который начинает прыгать по ним вниз,

к основанию.
Зайчик может прыгнуть на следующую ступеньку, на ступеньку через 1 или 2.
Определить число всевозможных “маршрутов” зайчика с вершины на землю.

с номером X.
По условию он может спрыгнуть на ступеньки

с номерами X - 1, X - 2 и X - 3.
Пусть F(X) - число маршрутов со ступеньки X до земли





F[X] = F[X – 1] + F[X – 2] + F[X – 3]

long long F[31];
cin>>N;
F[1]=1;F[2]=2;F[3]=4;
for(int i=4; i

return 0;
}

N
только вперед. Длина хода фишки не
более K (N, K

≤10).
Найти количество различных путей, по которым фишка может пройти поле от позиции 1 до позиции N.

по которым фишка может пройти поле от начала до

позиции с номером i. Предположим, что для любого j от 1 до i известны значения величин S[j]. Задача состоит в определении правила вычисления значения S[i+1], используя значения известных величин. Заметим, что в позицию с номером i+1 фишка может попасть из позиций i, i-1,...,i-k.
S[i+1]=S[i]+S[i-1]+...+S[i-k]
Вычисляя последовательно значения величин S[1], S[2],..., S[N] по правилу, получаем значение S[N] – решение задачи

к задачам, в которых требуется построить решение с максимизацией

или минимизацией, т.е. оптимальным значением некоторого параметра.

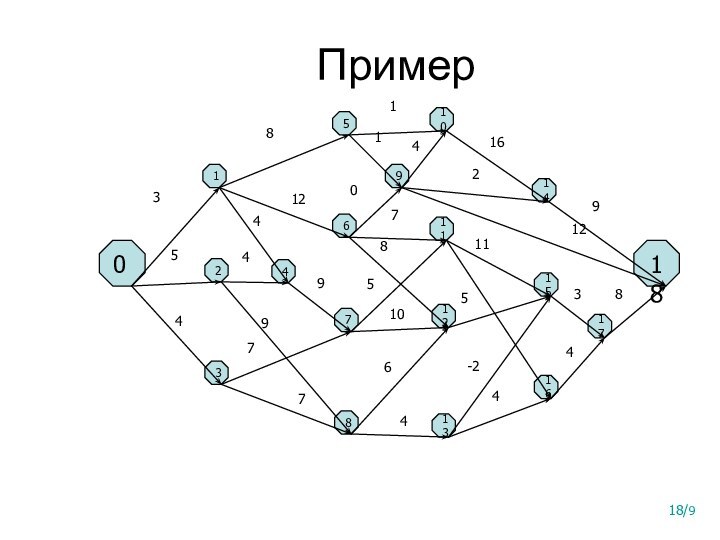
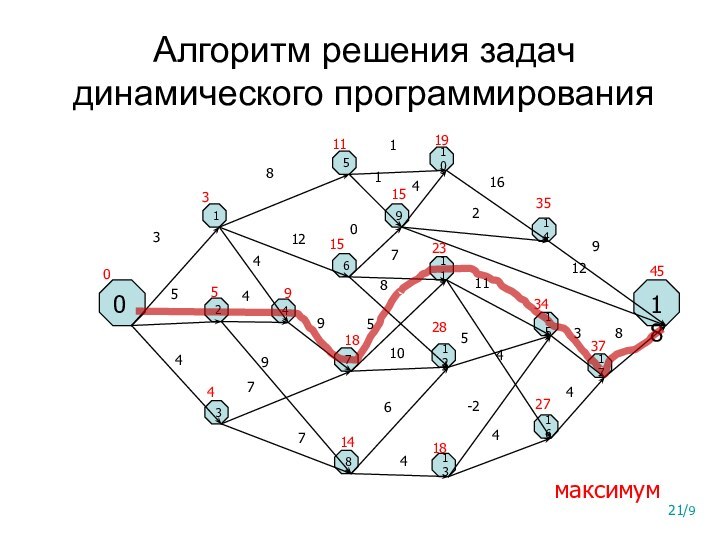
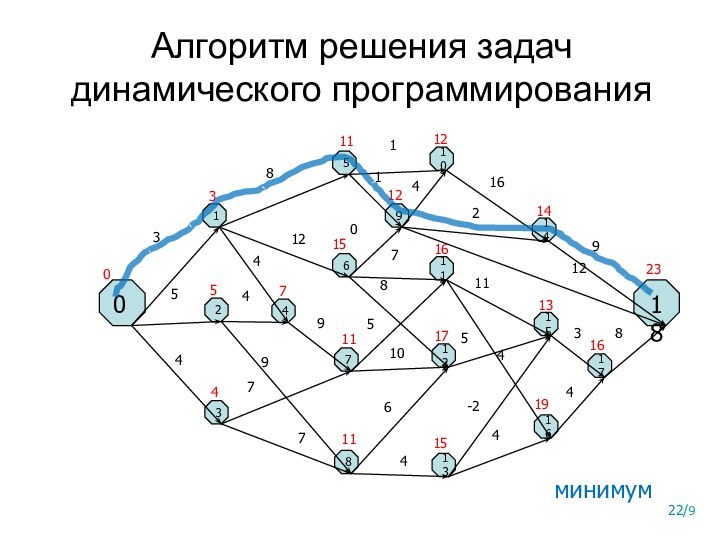
Его алгоритм можно сформулировать так:
Выделить и описать подзадачи, через решение которых будет выражаться искомое решение;
Выписать рекуррентные соотношения (уравнения), связывающие оптимальные значения параметра для всех подзадач;
Вычислить оптимальное значение параметра для всех подзадач;
Построить само оптимальное решение.

В задачах на подсчет количеств допустимых вариантов (задачи рассмотрены выше) пункт 4 не нужен

угла в правый верхний угол?

начальное и конечное
множество возможных переходов из одного состояния в

другое
с каждым переходом связывается числовой параметр
интерпретируется как затраты, выгода, расстояние, время и т.п.
Найти:
оптимальную последовательность переходов (путь) из начального состояния в конечное
максимум или минимум суммы числовых параметров
предполагается, что хотя бы один путь из начального состояния в конечное существует

/9

лежат на оптимальном пути между вершинами 0 и X,

то часть оптимального пути от 0 до X между вершинами A и B непременно является оптимальным путём от A до B.
Следствие
Чтобы найти оптимальный путь от 0 до A, достаточно исследовать продолжения к A всех оптимальных путей до вершин, предшествующих A
Продолжения неоптимальных путей к предшествующим вершинам можно не просчитывать: они никогда не дадут оптимального пути к A
Принцип Беллмана позволяет построить простую и эффективную вычислительную процедуру для решения задач динамического программирования

/9