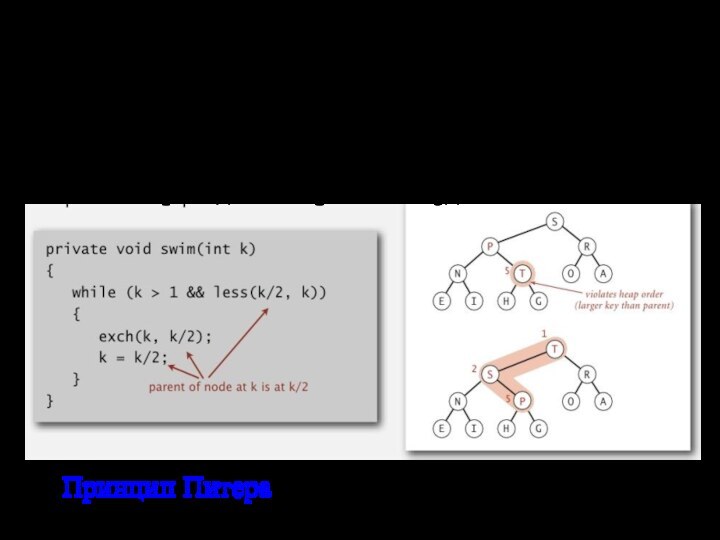
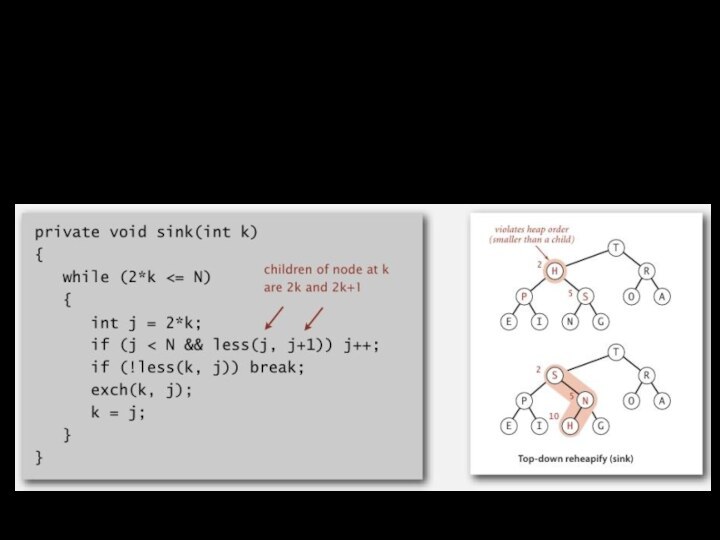
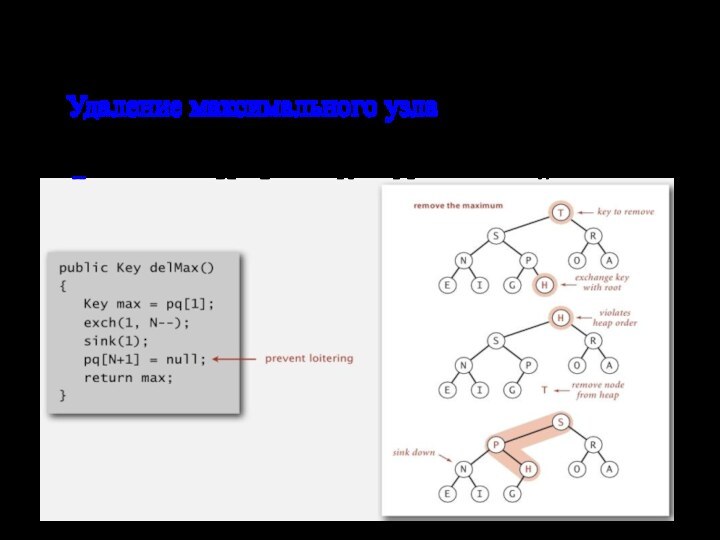
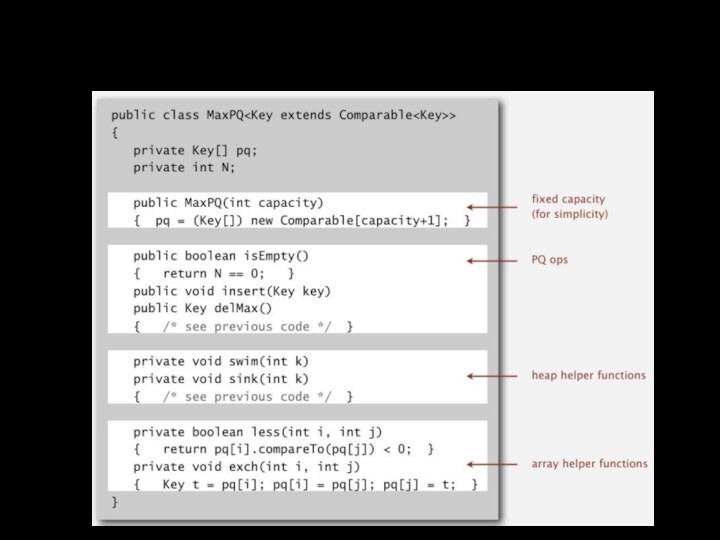
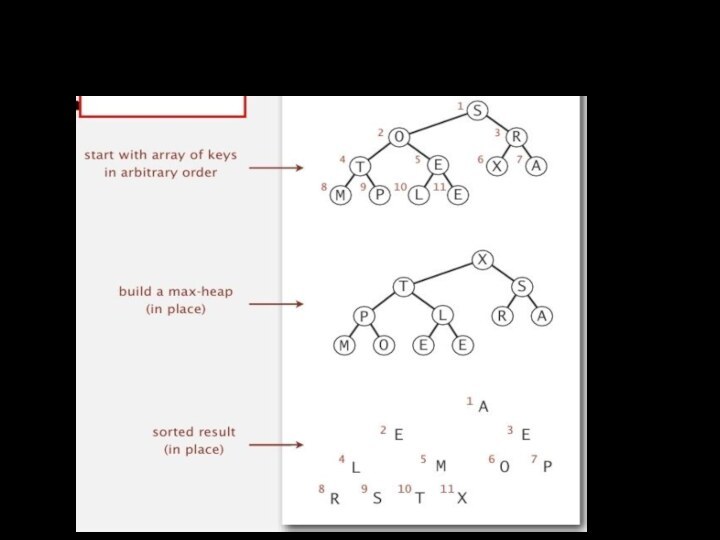
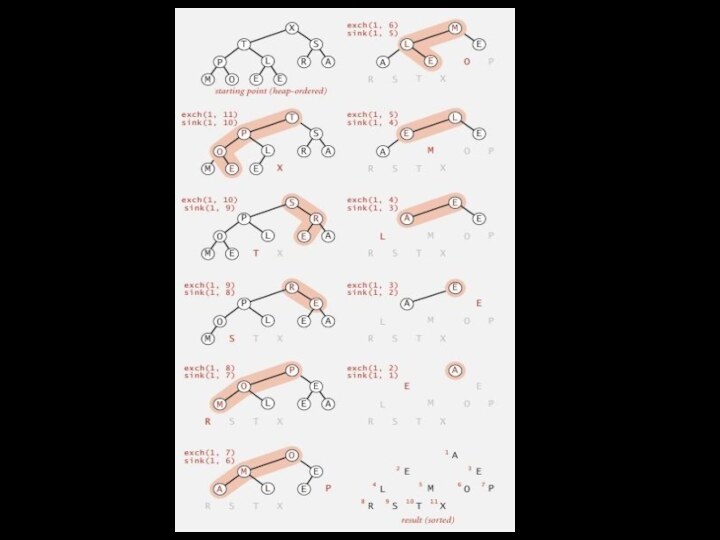
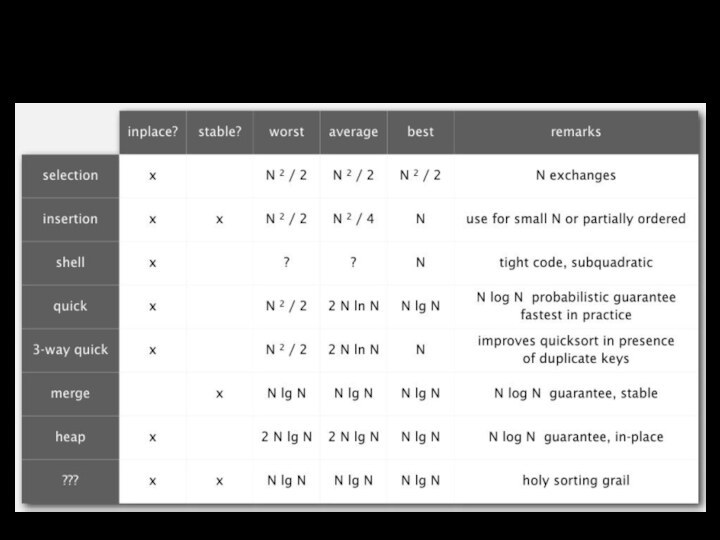
размер стека
Как увеличивать и уменьшать размер массива?
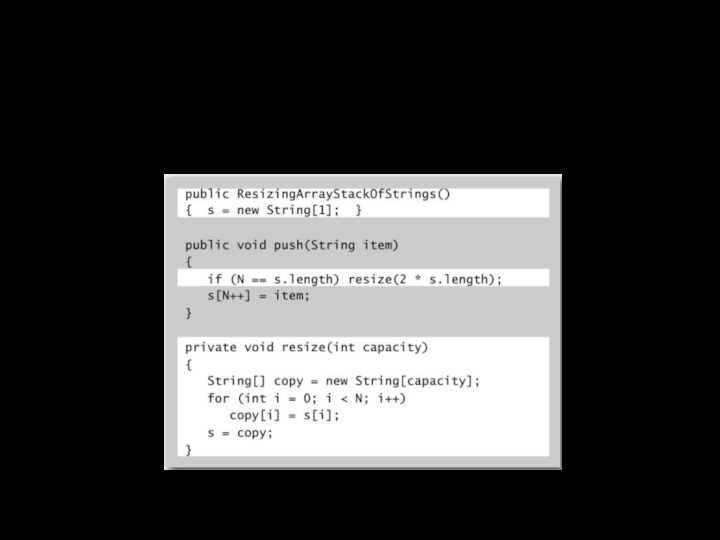
Первый подход
push(): увеличивать
размер массива s[] на 1pop(): уменьшать размер массива s[] на 1
Стоимость
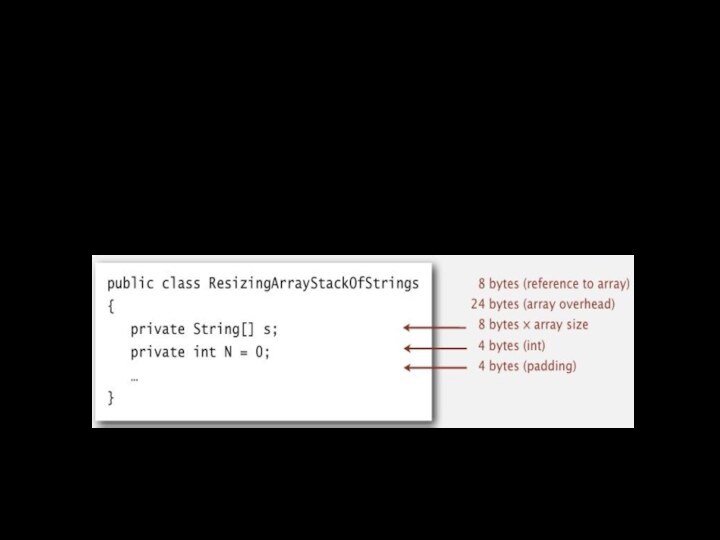
Требуется копировать все элементы в новый массив
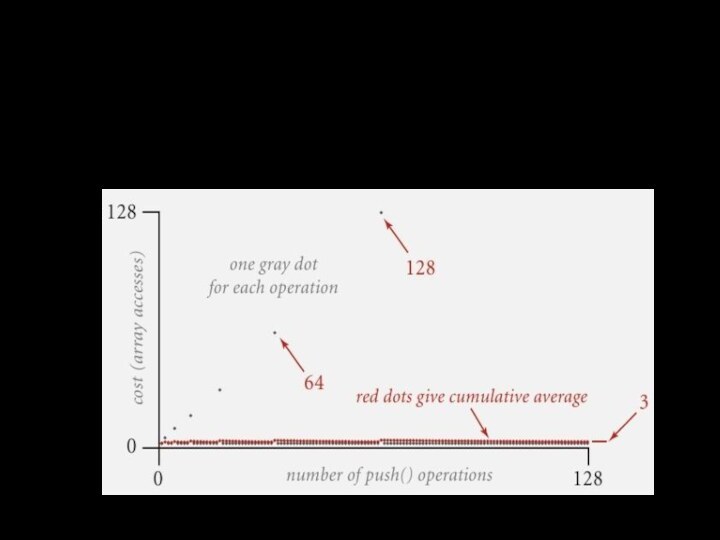
Сложность вставки первых N элементов 1+2+3+...+N ~ N2/2


![Изменение размера массива. Очередь с приоритетом. Бинарная пирамида. Пирамидальная сортировка Стек: изменение размера массиваКак изменять размер массива?Первый подходpush(): увеличивать размер массива s[]](/img/tmb/15/1454916/25575d87fc02ab8884b52cdd469aae0b-720x.jpg)
![Изменение размера массива. Очередь с приоритетом. Бинарная пирамида. Пирамидальная сортировка Стек: изменение размера массиваЭффективный подходpush(): увеличивать размер массива s[] в два раза,](/img/tmb/15/1454916/504ca8c6a5a2adced71727d9c36c9bfd-720x.jpg)













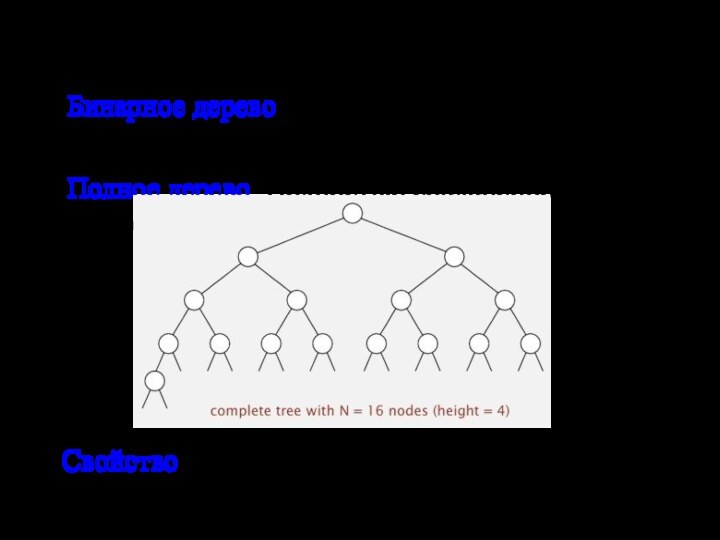

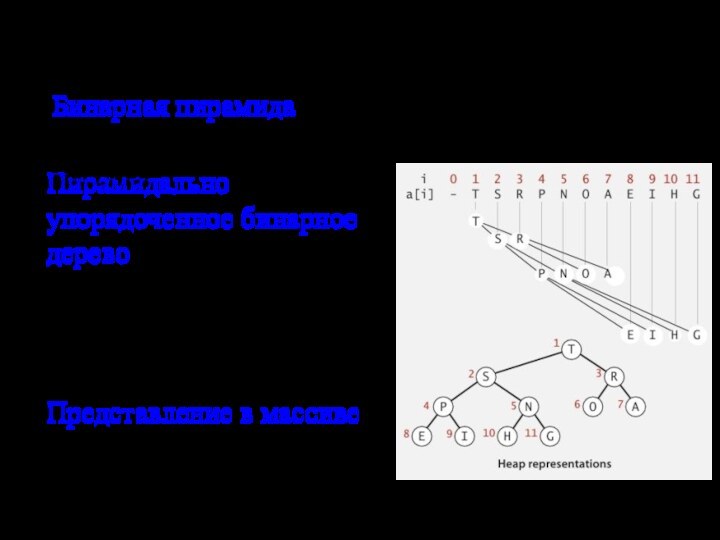
![Изменение размера массива. Очередь с приоритетом. Бинарная пирамида. Пирамидальная сортировка Бинарная пирамидаСамый большой ключ находится в корне по адресу а[1]Пользуйтесь индексами для](/img/tmb/15/1454916/803eb0f713db29c59d4104aa52c50ff2-720x.jpg)