Презентация на тему Работа с правильными многоугольниками в ЛогоМирах как пропедевтика решения задачи 6 ОГЭ по информатике.

фигуры. Они бывают плоскими, а бывают объемными. Сейчас вы

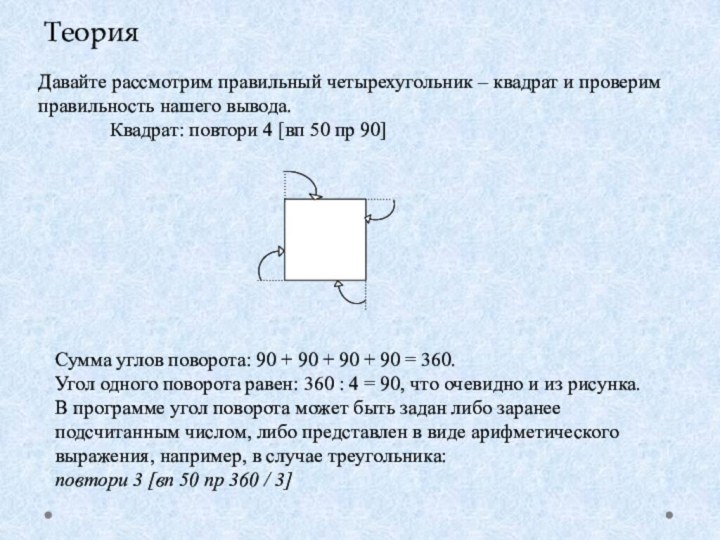
работаете с плоскими фигурами. А какие фигуры вы знаете? (Примеры). В треугольнике – 3 угла и 3 стороны. В четырехугольнике – 4 угла и 4 стороны. А как вы назовете фигуру, у которой много сторон и много углов? Правильно, многоугольник. Теперь подумайте, какой многоугольник называется правильным? (Правильным называется многоугольник, у которого все углы равны между собой и все стороны равны между собой). Приведите примеры известных вам правильных многоугольников. А можно ли ромб назвать правильным четырехугольником? Почему?
Рассмотрим, что такое правильный многоугольник с точки зрения Черепашки.
Попросим Черепашку нарисовать правильный многоугольник с количеством сторон 3, т. е. правильный треугольник.

Теория

длину стороны треугольника, должна повернуться на угол, отмеченный на

рисунке дугой. Мы сказали, что в любом правильном многоугольнике все углы его равны между собой. Поэтому и углы, отмеченные дугой, тоже равны между собой. Подсчитать величину этого угла можно на основе следующих рассуждений. Поскольку Черепашка, нарисовав треугольник, вернулась в исходное положение, значит она совершила суммарный оборот на 3600. Получается, что Черепашка, поворачиваясь 3 раза, нарисовала нужный нам треугольник и вернулась в исходное положение, сделав полный оборот в 3600.
Таким образом, чему же равен угол одного поворота? Как вы думаете, как его рассчитать?
Нужно величину полного оборота (3600) разделить на количество поворотов, т. е. на 3:
3600 : 3=1200
Следовательно, можно сделать вывод: при построении правильного многоугольника с количеством сторон n угол одного поворота b рассчитывается по следующей формуле:
b = 360 : n

Теория

правильность нашего вывода.
Квадрат: повтори 4 [вп 50 пр 90]

Сумма

углов поворота: 90 + 90 + 90 + 90 = 360.
Угол одного поворота равен: 360 : 4 = 90, что очевидно и из рисунка.
В программе угол поворота может быть задан либо заранее подсчитанным числом, либо представлен в виде арифметического выражения, например, в случае треугольника:
повтори 3 [вп 50 пр 360 / 3]

Теория

с помощью компьютера (садимся за компьютеры).
 Давайте построим правильный

18-угольник с длиной стороны 40 шагов (повтори 18 [вп 40 пр 20]) и рядом с ним, слева еще один многоугольник с количеством сторон 36 и длиной стороны 20 шагов. И пусть черепашка нарисует этот многоугольник, поворачиваясь налево: повтори 36 [вп 20 лв10].
Как вам кажется, на что похожи нарисованные фигуры? Правильно, на окружности. И чем больше сторон будет у многоугольника, тем больше он будет походить на окружность. Хотя если посмотреть на многоугольник как бы через лупу, его контур окажется не плавной линией, а ломаной. Действительно, ведь черепашка проходит несколько шагов вперед и поворачивает направо или налево. Если же шаг черепашки будет очень мал и угол поворота тоже будет маленьким, то тогда многоугольник будет как бы приближаться к окружности. С определенной погрешностью за окружность можно принять даже правильный 36-угольник. А что же такое окружность? (Окружность – это такая геометрическая фигура, все точки которой находятся на одинаковом расстоянии от ее центра.)

размера, которые на самом деле являются правильными многоугольниками с

количеством сторон, равным или более 36.
60-угольник со стороной 2 шага (повтори 60 [вп 2 пр 6])




2. 90- угольник со стороной 3 шага (повтори 90 [вп 3 пр 4])

Решение задач

1. n=60, b=6

2. n=90, b=4

120 [вп 4 пр 3])




4. 180- угольник со стороной

1 шаг (повтори 180 [вп 1 пр 2])



5. 360- угольник со стороной 2 шага (повтори 360 [вп 2 пр 1])

4. n=180, b=2

3. n=120, b=3

5. n=360, b=1

Решение задач

сторон n угол одного поворота b рассчитывается по формуле:
b

= 360 : n

2). За окружность можно принять правильный многоугольник с большим количеством сторон (36 и более) и небольшой длиной стороны.

Решение задач

правильный 10-угольник со стороной 20 шагов, нужно дать команду: 1.

повтори 20 [вп 10 пр 18]
2. повтори 10 [вп 20 пр 36]
II. Угол одного поворота
Правильный 36-угольник
Правильный 12-угольник
Правильный 9-угольник
Правильный 18-угольник

III. 15

В задании №1 нужно обвести цифру правильного ответа. В задании №2 в пустой столбец таблицы нужно вписать угол одного поворота для построения указанных многоугольников. В задании №3 нужно написать программу построения указанной фигуры.

повтори 6 [вп 15 пр 60]

100

300

400

200

Решение задач (рефлексия)

Пузыри на воде
Задание 4. Бабочка
Задачи для самостоятельного решения:
написать

программы рисования представленных фигур

8. Мышка
Задачи для самостоятельного решения:
написать программы рисования представленных

фигур

12. Зонтик
Задачи для самостоятельного решения:
написать программы рисования представленных фигур

повтори 180 [вп 1 лв 1]
Задание 2. Инь-янь
повтори 180

[вп 2 пр 2] повтори 180 [вп 1 пр 1] повтори 180 [вп 1 лв 1]

Задание 3. Пузыри на воде
повтори 180 [вп 4 пр 1] пр 180 повтори 180 [вп 3 пр 1] пр 180 повтори 180 [вп 2 пр 1] пр 180 повтори 180 [вп 1 пр 1]

Задание 4. Бабочка
повтори 120 [вп 3 пр 3] повтори 120 [вп 2 пр 3] повтори 120 [вп 1 пр 3]
повтори 120 [вп 3 лв 3] повтори 120 [вп 2 лв 3] повтори 120 [вп 1 лв 3]

Задание 5. Спираль
повтори 180 [вп 5 пр 1] повтори 180 [вп 4 пр 1] повтори 180 [вп 3 пр 1]
повтори 180 [вп 2 лв 1]

Задание 6. Цветок1
повтори 4 [повтори 180 [вп 3 пр 1] пр 90]

пр 1] лв 90]
Задание 8. Мышка
повтори 90 [вп 4

пр 2] лв 90 нд 57 вп 57 лв 90 повтори 90 [вп 1 пр 2]
повтори 90 [вп 1 лв 2]

Задание 9. Секира
повтори 180 [вп 2 пр 1] пр 180 повтори 90 [вп 2 лв 1]

Задание 10. Спираль2
повтори 4 [повтори 180 [вп 3 пр 1] повтори 180 [вп 1 пр 1] ]

Задание 11. Перо
повтори 180 [вп 4 пр 1] повтори 180 [вп 2 пр 1] повтори 180 [вп 2 лв 1]

Задание 12. Зонтик
повтори 180 [вп 3 пр 1] повтори 180 [нд 2 лв 1] повтори 90 [вп 1 лв 1] лв 90
вп 100 повтори 180 [вп 1 пр 1] пр 1 повтори 180 [нд 1 лв 1] нд 100 лв 90
повтори 90 [вп 1 лв 1] повтори 180 [нд 4 лв 1]