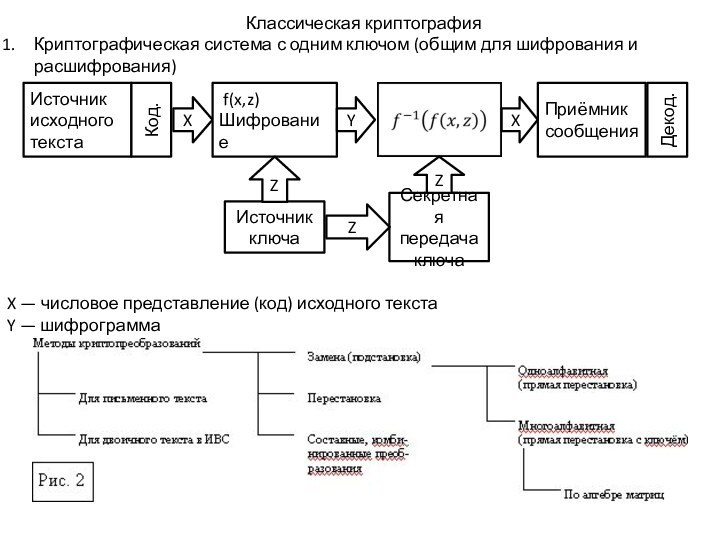
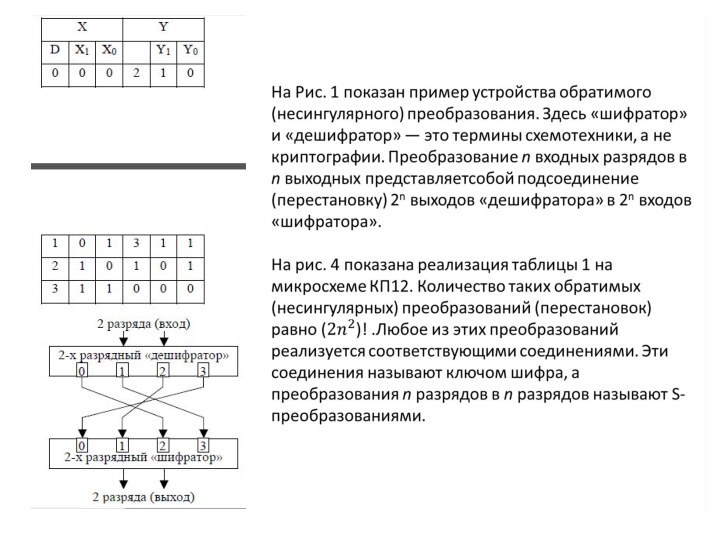
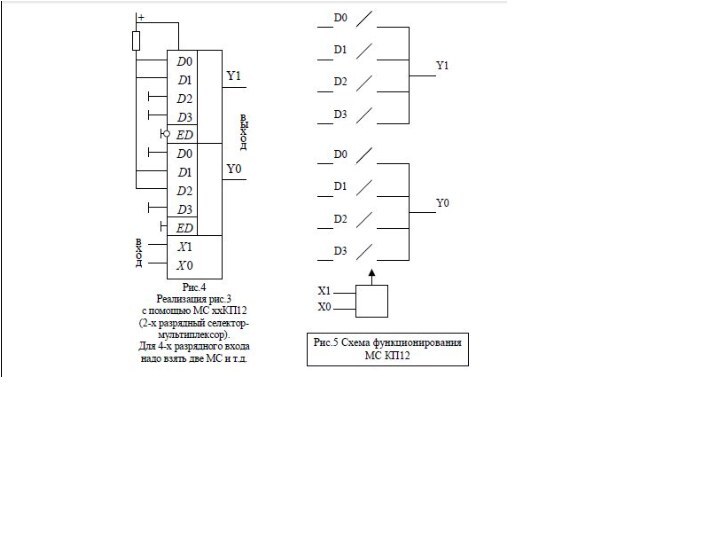
Слайд 2
Шифрование заменой (подстановками)
Моно(одно)алфавитная замена — самый простой способ

прямой замены. Составляется таблица прямой замены букв шифруемого текста
другими буквами данного алфавита.
Таблица замены
Знаки в таблице шифрования не должны повторяться, т.е. таблица замены должна представлять полную перестановку алфавита (когда все буквы подверглись перестановке). После замены шифротекст для удобства работы с ним разбивается на равновеликие группы. В шифре Цезаря таблица замены есть алфавит сдвинутый в кольцо на 3 позиции.
Одноалфавитный шифр имеет низкую стойкость. Сравнительно легко взламывается, т.к. имеет те же статистические характеристики частости букв в шифрограмме, что и в исходном (открытом) тексте. При достаточной длине шифротекста он раскрывается статистическим криптоанализом.
Многотабличная замена. Буквенная ключевая последовательность.
Многоалфавитный шифр более стойкий. Например, таблица Вижинера. Это квадратная матрица N*N, где N — количество символов алфавита.
Первая строка матрицы — исходный алфавит. Следующие — кольцевой сдвиг алфавита на одну букву. Для шифрования задаётся слово из K букв (буквенный ключ). Из таблицы Вижинера выписывается рабочая подтаблица (K+1)*N. Первая строка — исходный алфавит.
Следующие строки — алфавиты, начинающиеся с очередных букв ключа. Процедура шифрования:
Слайд 5
Если в многоалфавитной подстановке:
Число знаков в ключе больше

(или равно) числу шифруемых (исходных) знаков текста и знаки
в ключе распределены случайно
Ключ используется только один раз
Исходный текст (или его часть) неизвестен злоумышленнику (криптоаналитику), то зашифрованный текст будет нераскрываем и называется системой (схемой) Вернама.
Именно для этих условий Шеннон Э. и доказал нераскрываемость шифра.
Если криптоаналитику известен (или предполагается известным) отрезок исходного текста заведомо в несколько раз длиннее ключа, то ключ будет раскрыт вычитанием из шифрограммы известного отрезка текста
z = {у - x)mo6.N
перебором знакоместа шифрограммы для начала серии вычитаний. Появление периодической структуры результата и есть признак вскрытия ключа.
С этой позиции рассмотрим известное усовершенствование таблицы Вижинера. Во всех строках, кроме первой буквы алфавита располагаются в произвольном порядке (а не сдвигаются), т.е. используется множество перестановок букв алфавита. Число перестановок P(N) = N\, Р(27) = 1.088 -1028. Однако, из этого множества не так много подходящих, нужны только «полные» перестановки, т.е. такие которые затронули все буквы алфавита. Вот из этого множества и выбираем 10 (не считая первой) перестановок.
Слайд 6
Нумеруем их натуральными числами 0, 1, ..., 9.
В
качестве ключа берём случайный (практически псевдослучайный) ряд чисел бесконечной
длины или длины не меньшей, чем количество букв исходном тексте. Например: л =3.14159265358979323846..., е =2.71828182845904523536...
При длине ключа равной длине текста статистическая закономерность букв исходного алфавита, по - видимому, полностью маскируется.
Однако это всё таки всего 10-алфавитный ключ, правда алфавиты чередуются на всём протяжении текста в «случайном» порядке, а не повторяются группами по слову текстового ключа. Стойкость шифра несколько усиливается.
Формула (1) даст ещё лучшую стойкость, если в ней в качестве последовательности ключа взять «случайные» (например, по таблице случайных чисел 2-хразрядных десятичных) из множества 0, 1, 2, ..., (N -1).
В этом случае получим 27-алфавитную подстановку со «случайным» чередованием алфавитов на всём протяжении исходного текста.
Слайд 12
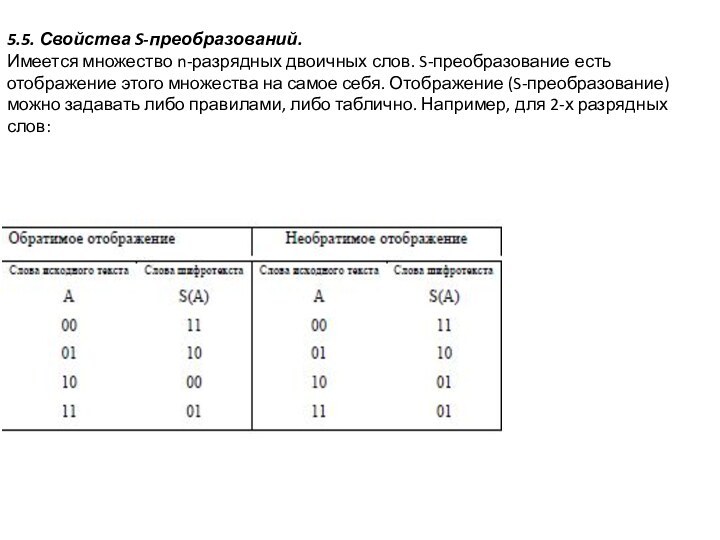
5.5. Свойства S-преобразований.
Имеется множество n-разрядных двоичных слов. S-преобразование
есть отображение этого множества на самое себя. Отображение (S-преобразование)
можно задавать либо правилами, либо таблично. Например, для 2-х разрядных слов:
Слайд 14
Метод перестановок (шифрование перестановками)
Исходный текст разбивается на ключевые
группы с равными количествами букв в группах. В каждой
группе по заданному правилу производится перестановка букв.
Табличный вариант
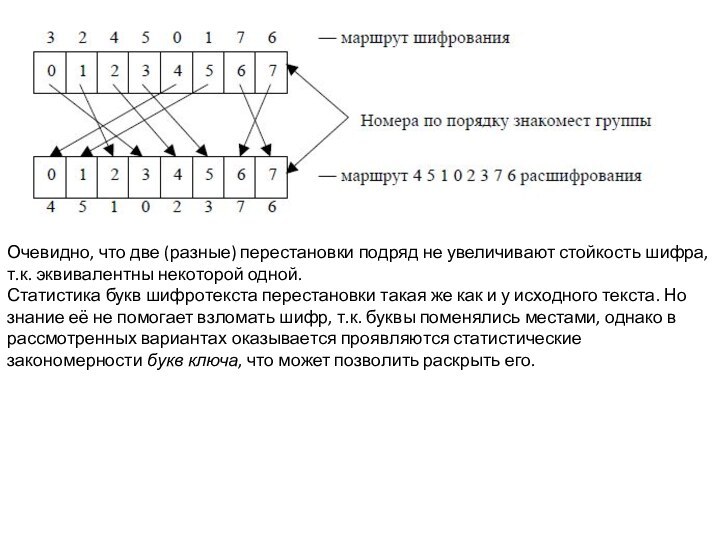
Записываем исходный текст по строкам в матрицу из N столбцов. Затем шифруем текст переставляя столбцы матрицы в заданном порядке перестановок. Этотпорядок перестановок есть ключ (и операция) перестановок. Заданный порядок перестановок можно выразить осмысленным словом (ключом) с неповторяющимися буквами и
производить шифрование, т.е. перестановку колонок таблицы в той последовательности, в которой располагаются в алфавите буквы ключевого слова.
Слайд 15
Получаем, читая по столбцам в порядке перестановок следующую
шифровку: РПАМУЕНИШТЕВИЕСКФЁТАЙРОЬ или группами по 6 букв:
РПАМУЕ
НИШТЕВ ИЕСКФЁ ТАЙРОЬ
Расшифровка
Определяем число колонок, деля количество знаков в шифрограмме на число букв в ключе 30/6 = 5.
Выписываем ключевое слово с обозначением последовательности букв ключа в алфавите и под ними в колонки с указанной последовательностью выписываем текст шифровки. Открытый текст читаем по строкам.
Усложнение табличного варианта.
Шифруемый текст вписываем в таблицу выбранной размерности по некоторому маршруту, например по спирали. Затем колонки выписываем либо подряд, либо переставляя по ключу. Расшифровываем в обратной последовательности.
Слайд 16
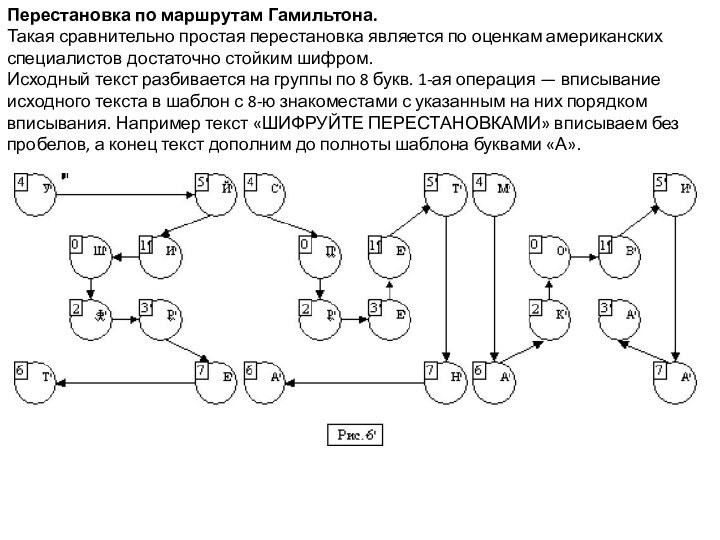
Перестановка по маршрутам Гамильтона.
Такая сравнительно простая перестановка является
по оценкам американских специалистов достаточно стойким шифром.
Исходный текст разбивается
на группы по 8 букв. 1-ая операция — вписывание исходного текста в шаблон с 8-ю знакоместами с указанным на них порядком вписывания. Например текст «ШИФРУЙТЕ ПЕРЕСТАНОВКАМИ» вписываем без пробелов, а конец текст дополним до полноты шаблона буквами «А».
Слайд 17
2-ая операция — последовательное повторение 5-ти разных маршрутов
Гамильтона. На рисунках нам хватило 3-х маршрутов. Выписываем по
этим маршрутам шифрограмму:
УЙИШФРЕТ СПРЕЕТНА МАКОВИАА
1-я перестановка 2-я перестановка 3-я перестановка
Для перестановки букв в группах по 8 количество разных перестановок (маршрутов) М= Р(8) = 8!=40320. Количество возможных перестановок быстро увеличивается с ростом длины группы перестановок.
Если злоумышленник угадает длину группы, то он может перебрать последовательно все возможные перестановки пока не найдёт осмысленную. Для малой длины группы это легко особенно с помощью ЭВМ. Посмотрим как усложняется этот пример с ростом длины группы.
Слайд 18
Количество M перестановок для группы из N букв
равно: М = P(N) = N! Перестановки удобно задавать
числовыми ключами (гаммами) Так перестановки Гамильтона будутиметь вид:
Расшифрование производится в обратном порядке (двигаться в направлении обратном стрелке перестановки), т.е. ключи перестановки для расшифрования будут: Перепишем ключи шифрования в виде