Презентация на тему Кодирование числовой информации. Системы счисления. Представление чисел в компьютере

посредством некоторого алфавита символов, называемых цифрами.

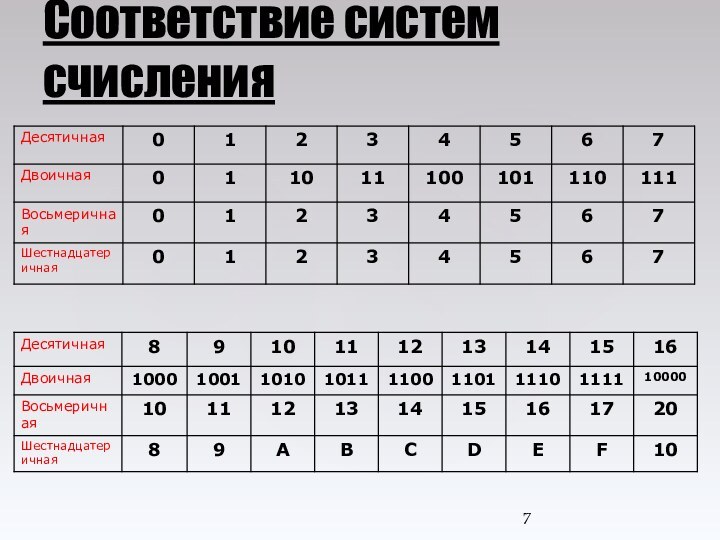
Как известно, системы счисления

(СС) бывают позиционные и непозиционные.

В позиционной системе счисления в зависимости от положения(разряда) в котором находится число оно имеет разное значение. Например: 123 (“1”- сотни,”2”- десятки,”3”-единицы)

В непозиционных системах счисления число не меняет своего значения в зависимости от позиции. Например: XXV, XVI, VII(V везде значит – 5)

Системы счисления, применяемые для представления числовых данных в ЭВМ

счисления. Числа хранятся в оперативной памяти в виде последовательностей

нулей и единиц, т.е. в двоичном коде.

последовательности цифр: А = аm-1 аm-2…а1 а0, а-1 а-2

а-3…а-n. (1) Записанную выше последовательность цифр (1), соответствующую числу А, можно представить в виде полинома (2) от основания q: A=am-1+qm-1+am-2*qm-2+…+a1*q1+a0*q0+a-1*q-1+a-2*q-2+…+a-n*q-n (2) Основание системы счисления определяет ее название, например, q = 10 – десятичная система счисления, а q = 2 – двоичная. В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.

Системы счисления, применяемые для представления числовых данных в ЭВМ

СС - (А)8, шестнадцатеричная СС - (А)16.
Системы счисления, применяемые

для представления числовых данных в ЭВМ

(знаков) в ее алфавите
Позиция цифры в числе называется

разрядом

с (1) и (2) может быть представлено последовательностью двоичных

цифр (3) или суммой степеней числа 2, взятых с указанными в ней коэффициентами (4). Х = аm-1 аm-2… а1 а0, а-1 а-2 а-3…, (3) где ai = {0,1};  X=am-1*2m-1+…+a1*21+a0*20+a-1*2-1+a-2*2-2+…+a-n*2-n (4) Например, двоичное число 1010,001 будет представлено следующим образом: (1110,001)2=1*23+1*22+1*21+0*20+0*2-1+0*2-2+1*2-3

Системы счисления, применяемые для представления числовых данных в ЭВМ

Любое число в восьмеричной системе может быть представлено последовательностью

цифр или суммой степеней числа 8.   . В шестнадцатеричной системе счисления для изображения чисел употребляются 16 цифр от 0 до 15. При этом, чтобы одну цифру не изображать двумя знаками, введены обозначения для цифр, больших девяти, латинскими буквами: десять – А, одиннадцать – В, двенадцать – С, тринадцать - D, четырнадцать – Е, пятнадцать – F.

Системы счисления, применяемые для представления числовых данных в ЭВМ

счисления с основанием q, в систему счисления с основанием

S необходимо данное число и получаемые частные последовательно делить на новое основание системы счисления до тех пор, пока последнее частное не будет меньше S. Число А в системе счисления с основанием S представится в виде упорядоченной последовательности остатков деления, причем старшую цифру дает последнее частное. (12)10 = (1100)2

Перевод целых чисел

на основание новой системы счисления, причем перемножению подвергаются только

дробные части результата. Дробь в новой системе счисления представляется в виде упорядоченной последовательности целых частей произведений, где старший разряд является первой цифрой произведения. (0,325)10 = (0,0101)2

Перевод дробных чисел

цифру числа заменить трехразрядным двоичным числом. При этом отбрасывают

нули, стоящие слева от старшей значащей цифры и справа от младшей значащей цифры двоичного кода. (175,6)8 = (125,75)10 , (1111101,11)2 = (125,75)10

ПЕРЕВОД (А)8 (А)2

каждую цифру числа четырехразрядным двоичным кодом. (2CF,5)16 = (1011001111,0101)2
ПЕРЕВОД

(А)16 (А)2

двоичного числа 111000110,101 в шестнадцатеричное
ПЕРЕВОД (А)2

(А)8 и (А)2 (А)16

(точки) фиксировано относительно разрядов числа и сохраняется неизменным для

всех чисел.
Запятая отделяет целую часть числа от дробной.
Если дробная часть отсутствует, то число – целое.

Для кодирования знака используется знаковый разряд
(«0» для положительных чисел и «1» – для отрицательных).

Представление двоичных чисел в форме с фиксированной запятой

в компьютере хранятся в памяти в формате с фиксированной запятой.

В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т.е. вне разрядной сетки.



Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 бит). Например, число A2 = 101010102  будет хранится в ячейке памяти следующим образом:
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно:
2n - 1

бит), причем старший (левый) разряд отводится под знак числа

(если число положительное, то в знаковый разряд записывается 0, если число отрицательное записывается 1).
Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа. Например, число 200210 = 111110100102 будет представлено в 16-ти разрядном представлении следующим образом:

довольно простой алгоритм:
1.        Модуль числа записать прямым кодом в n двоичных разрядах;
2.        Получить обратный код числа, для

этого значения всех бит инвертировать (все единицы заменить на нули и все нули заменить на единицы);
3.        К полученному обратному коду прибавить единицу.
Пример. Записать дополнительный код отрицательного числа –2002 для 16-ти разрядного компьютерного представления с использованием алгоритма.

для представления числа со знаком выделено n разрядов, то

диапазон представления целых двоичных чисел в этом случае определяется выражением


Диапазон представления в ЭВМ дробных двоичных чисел будет определяться неравенством



или приближенно

для представления соответственно целого двоичного числа ( = +11000)

и дробного числа ( = +0,11) в форме с фиксированной запятой:

Представление двоичных чисел в форме с фиксированной запятой

число (Х)2 в формате (n=7 со знаком):



Целое число

(Х)2 в формате (n=8 со знаком):



Дробное число (Х)2 в формате (n=8 со знаком):

Представление двоичных чисел в форме с фиксированной запятой

и обрабатываются в компьютере в формате с плавающей запятой. В

этом случае положение запятой в записи числа может изменяться.
Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любой число. Так число А может быть представлено в виде:
 
A = m×qn
где    m – мантисса числа
         q – основание системы счисления,
         n – порядок числа.
Для однозначности представления чисел c плавающей запятой  используется нормализованная форма, при которой мантисса  отвечает условию:
1/n ≤ |m| < 1.
Это означает,  что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.

Представление двоичных чисел в форме с плавающей запятой

разрядом. Порядок Р указывает положение запятой в числе, может

быть положительным или отрицательным целым числом или целым числом без знака (запятая при представлении порядка фиксируется после младшего разряда). Порядок Р и мантисса mn представляются в системе счисления с основанием q.

Представление двоичных чисел в форме с плавающей запятой

своим знаком:

А1 = +0,0101, [А1]пр = 00101;
А2 = – 0,0101, [А2]пр = 10101.

Для целых чисел в двоичной системе счисления:
А1 = + 1100, [А1]пр = 01100;
А2 = – 1100, [А2]пр = 11100.

Нуль в прямом коде имеет два изображения:
+ 0 = 000…00 = [0]пр,
– 0 = 100…00 = [0]пр

Кодирование отрицательных чисел в ЭВМ

обратном коде, нужно поставить в знаковый разряд единицу, а

все остальные разряды инвертировать:
А = – 0,1010. [А]обр = 10101.
Примеры обратного кода отрицательных дробного и целого чисел:

Aдр=-0,11001;
[Aдр]пр = 111001;
[Aдр]обр=100110;

Aц = -10101;
[Aц]пр = 110101;
[Aц]обр= 101010;

Кодирование отрицательных чисел в ЭВМ

коде нужно поставить единицу в знаковом разряде, затем найти

крайнюю правую единицу и заменить на противоположные разряды слева (до знака). Остальное не менять.
Примеры:

Кодирование отрицательных чисел в ЭВМ

дополнительный:
дополнительный код отрицательного числа может быть получен из

обратного путем прибавления к нему единицы младшего разряда.
Примеры:

[A]пр = 1.01010; [A]пр =1.11101;
[A]обр = 110101; [A]обр = 100010;
[A]доп = 110110, [A]доп =100011.


Отрицательный нуль изображается:
- в обратном коде [–0]обр = 1.11111…11;
- в дополнительном коде отрицательный нуль отсутствует, т.е. код нуля в дополнительном коде соответствует коду нуля положительного числа.

Кодирование отрицательных чисел в ЭВМ

обратном и дополнительных кодах имеют
одинаковую форму записи!!!