Презентация на тему Методы типа ветвей и границ

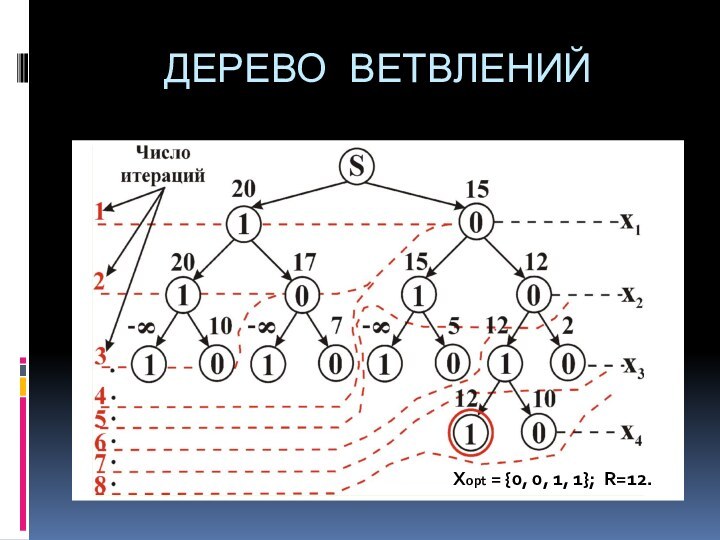
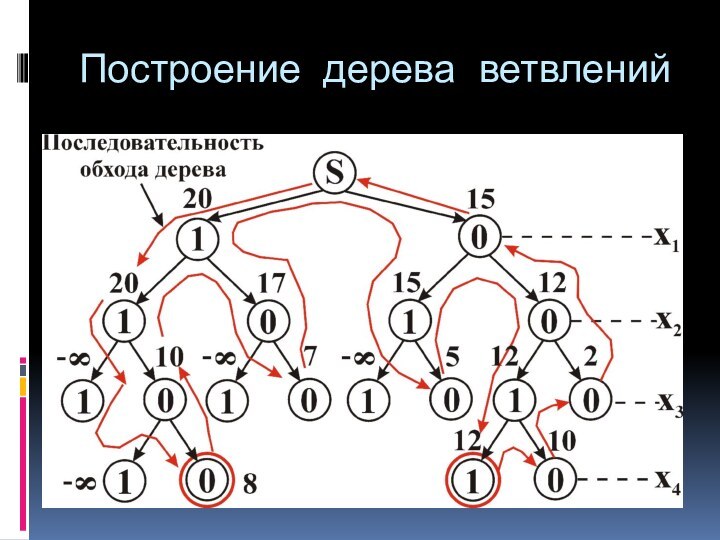
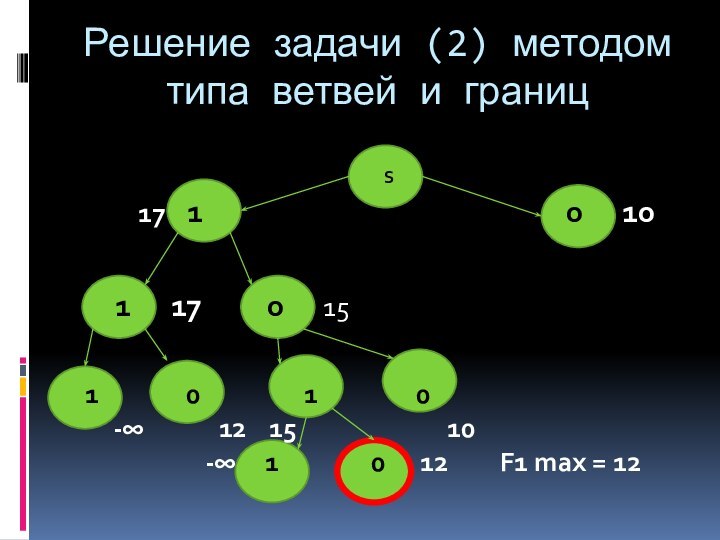
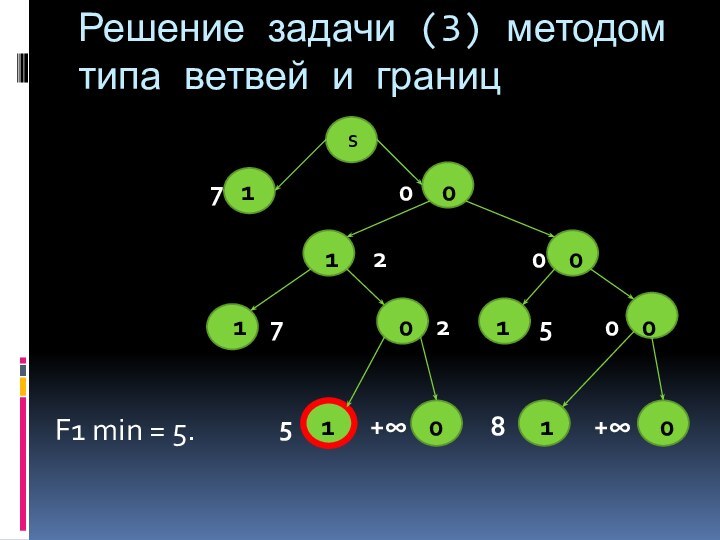
дереву ветвлений
1.2. Поиск с возвратом (алгоритм Балаша)
2. Многокритериальные задачи
 2.1.Поиск

величин эталонов методами типа ветвей и границ.
2.2. Формальная постановка задачи.
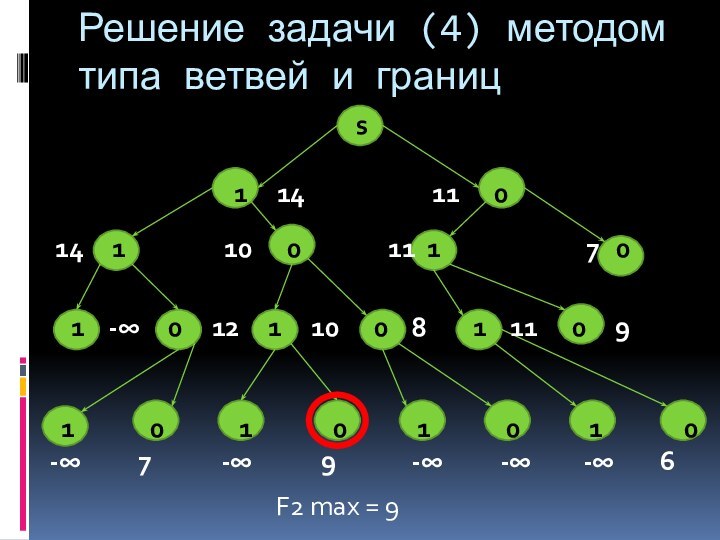
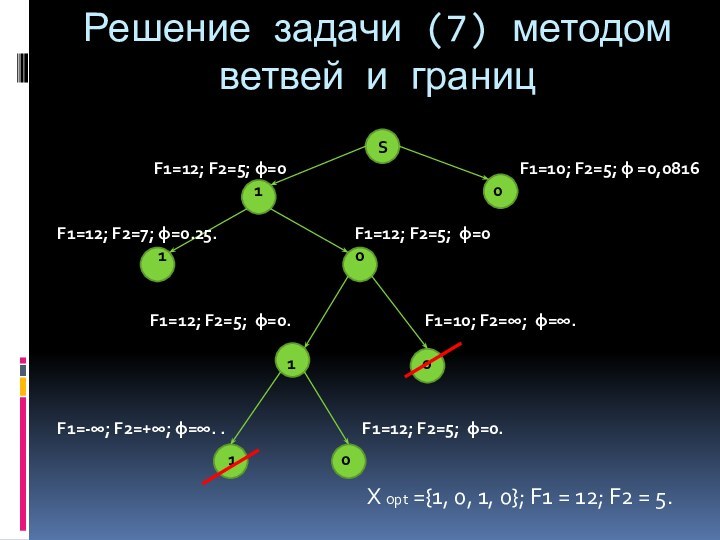
2.3. Решение многокритериальной задачи методом типа ветвей и границ.


 

вычисления оценки таков, что по мере спуска по дереву

ветвлений оценка не улучшается.
2. Спуск по дереву ветвлений прекращается, если выбранная вершина обладает следующими свойствами:
оценка этой вершины является наилучшей;
существует возможность определить значения всех переменных, причем оценка остается неизменной.

ветвлений выбирается вершина с наилучшей оценкой, принадлежащая i-у ярусу.
Шаг

2. Если i=n, где n – число переменных, то перейти к шагу , в противном случае – к шагу 3.
Шаг 3. В базис частичного плана, соответствующего выбранной вершине, вводится (i+1)-я переменная и вычисляются соответствующие оценки. Перейти к шагу 1.
Шаг 4. Конец алгоритма. Оценка выбранной на предыдущем шаге вершины является оптимальным значением целевой функции.

шанс на неполный перебор, первый же полный допустимый план

является глобально оптимальным.
Недостатки: по мере спуска по дереву ветвлений растет число оценок, хранимых в памяти и затраты времени на их сравнение при выборе направления спуска.
 

2. i = 1
Шаг 3. xi = 1
Шаг 4.

Вычисляется оценка рекорда F
Шаг 5. Если F R, то перейти к шагу 6, нет –
к шагу 9
Шаг 6. Если все ограничения удовлетворяют, то
перейти к шагу 7, нет к шагу 9
Шаг 7. Если i = n, то перейти к шагу 8, нет –
к шагу 13
Шаг 8. R = F, печать R и вектора
Шаг 9. Если xi = 1, то перейти к шагу 10, нет –
к шагу 13
Шаг 10. xi = 0, перейти к шагу 4
Шаг 11. Если i = 1, то перейти к шагу 14, нет к шагу 12.
Шаг 12. i = i - 1, перейти к шагу 9.
Шаг 13. i = i + 1, перейти к шагу 3.
Шаг 14. Конец алгоритма. Последние выданные на печать значения R и , оптимальны.

с возвратом, решить задачу вида:
 

границ

новую целевую функцию вида:





где Fi - i– я целевая

функция, zi = 1, если Fi max,
и zi = 0, если Fi min.

задачу с булевыми переменными вида:

задачу, следует определить максимальные и минимальные значения F1 и

F2.

S

17 1 0 10


1 17 0 15



1 0 1 0
-∞ 12 15 10
-∞ 1 0 12 F1 max = 12

(3):

S

7 1 0 0

1 2 0 0

1 7 0 2 1 5 0 0


5 1 +∞ 0 8 1 +∞ 0

F1 min = 5.

s

1 14 11 0

14 1 10 0 11 1 7 0


1 -∞ 0 12 1 10 0 8 1 11 0 9


1 0 1 0 1 0 1 0
-∞ 7 -∞ 9 -∞ -∞ -∞ 6

F2 max = 9

S

3 1 0 0

7 3 4 0

1 0 1 0

5 3 6 4 2 0

1 0 1 0 1 0



+∞ +∞ +∞ +∞ 7 + ∞ 5 +∞

1 0 1 0 1 0 1 0

F2 min = 5

S
F1=12; F2=5; φ=0 F1=10; F2=5; φ =0,0816
1 0

F1=12; F2=7; φ=0.25. F1=12; F2=5; φ=0
1 0


F1=12; F2=5; φ=0. F1=10; F2=∞; φ=∞.

1 0


F1=-∞; F2=+∞; φ=∞. . F1=12; F2=5; φ=0.

1 0

X opt ={1, 0, 1, 0}; F1 = 12; F2 = 5.