- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Моделирование фракталов в Maxima
Содержание
- 2. Что такое фракталы
- 3. Обладает сложной структурой при любом увеличении;Является (приближенно)
- 4. Обзор пакета fractalsтреугольник Серпинского, фракталы «Дерево», «Папоротник»;
- 5. Функции пакета fractals
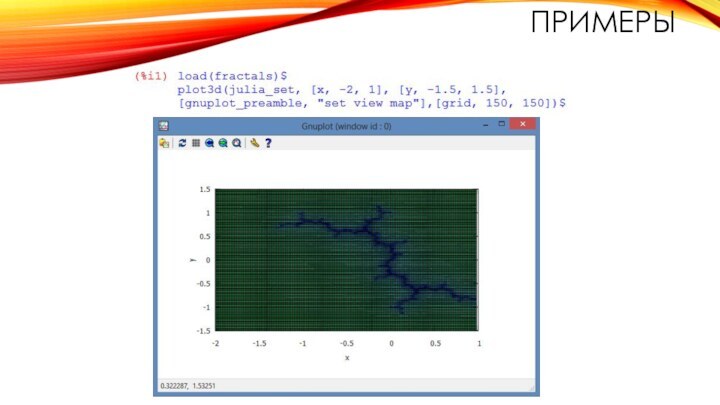
- 6. Примеры
- 7. Примеры
- 8. Примеры
- 9. Примеры
- 10. Обзор пакета dynamicsпаутинная диаграмма;бифуркационная диаграмма;эволюция орбиты одно-
- 11. Функции пакета dynamics
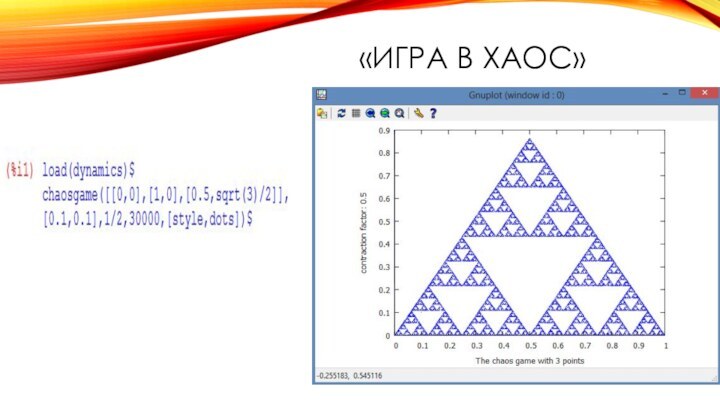
- 12. «игра в хаос»
- 13. Построение аттрактора системы итерированных функций
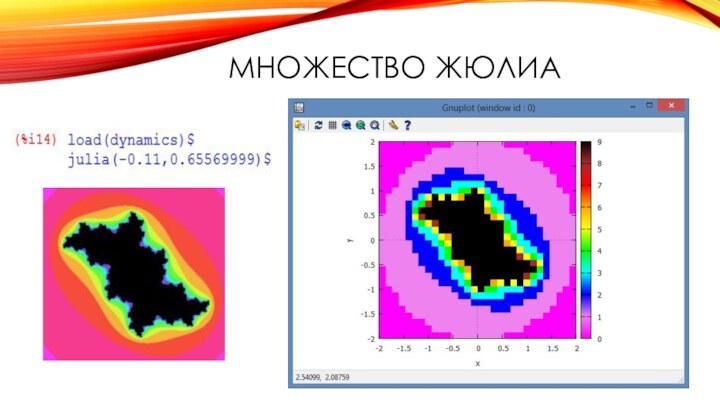
- 14. множествo Жюлиа
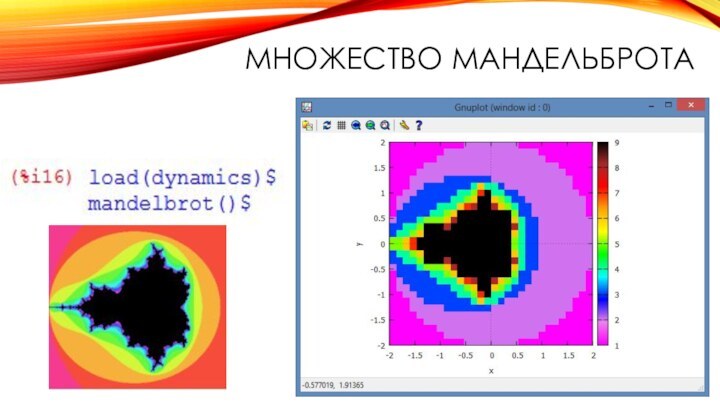
- 15. Множество Мандельброта
- 17. Скачать презентацию
- 18. Похожие презентации
Что такое фракталы









Слайд 3
Обладает сложной структурой при любом увеличении;
Является (приближенно) самоподобной;
Обладает
дробной хаусдорфовой(фрактальной) размерностью, которая больше топологической;
процедурами
Слайд 4
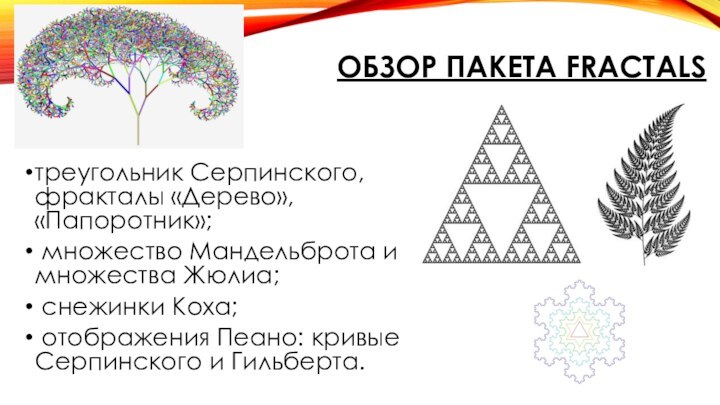
Обзор пакета fractals
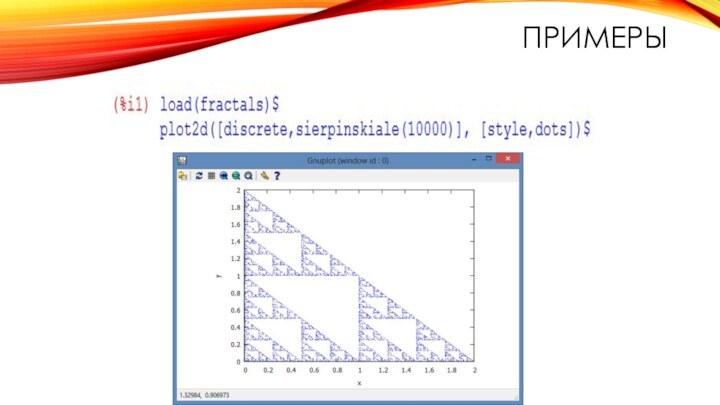
треугольник Серпинского, фракталы «Дерево», «Папоротник»;
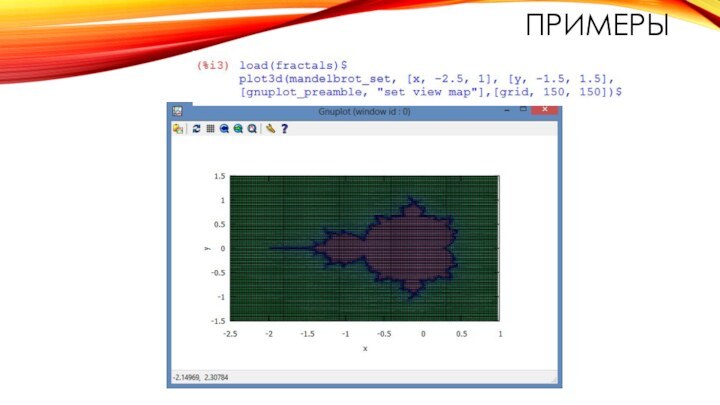
множество Мандельброта и множества Жюлиа;
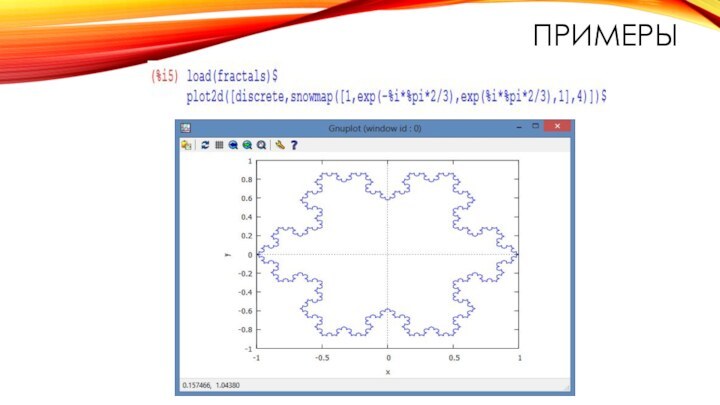
снежинки Коха;
отображения Пеано: кривые Серпинского и Гильберта.
Слайд 10
Обзор пакета dynamics
паутинная диаграмма;
бифуркационная диаграмма;
эволюция орбиты одно- и
двумерного отображений;
«игра в хаос»;
система итерированных функций, заданная
аффинными преобразованиями; множества Жюлиа, Мандельброта;





























