Презентация на тему Моделирование и формализация

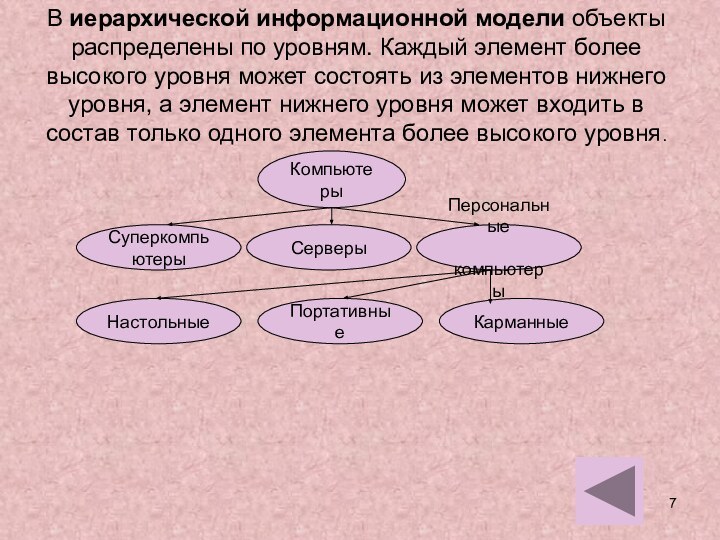
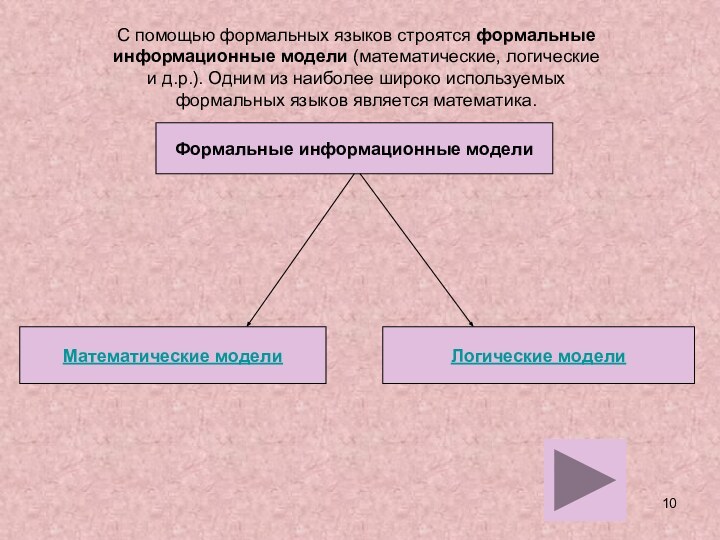
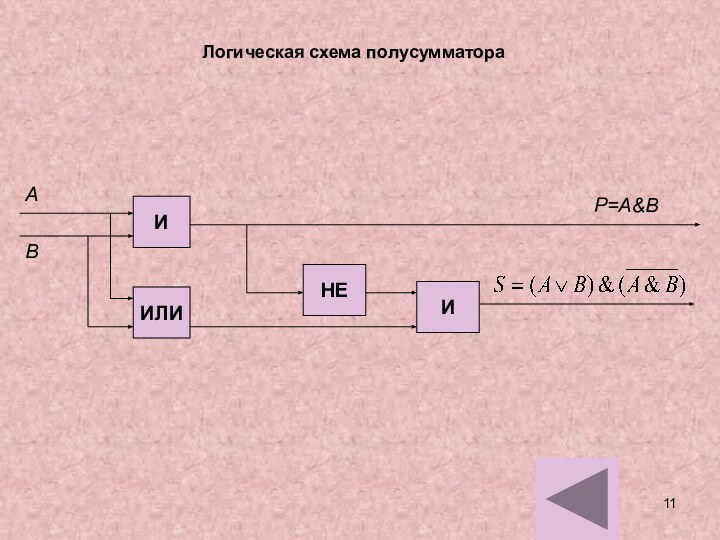
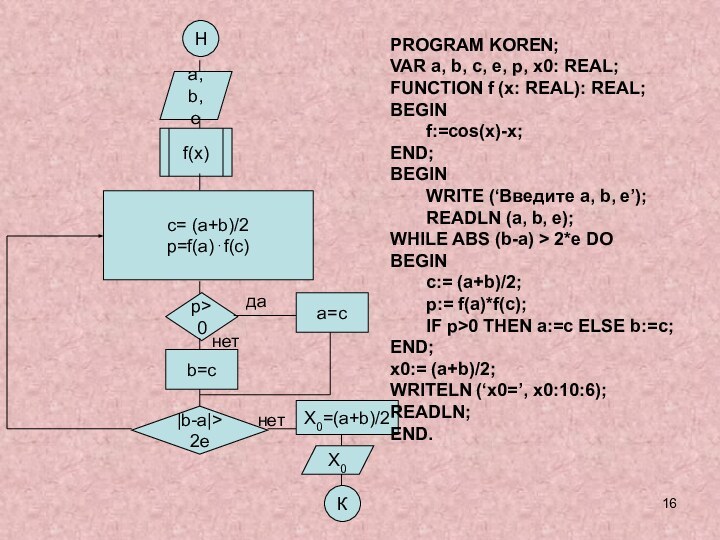
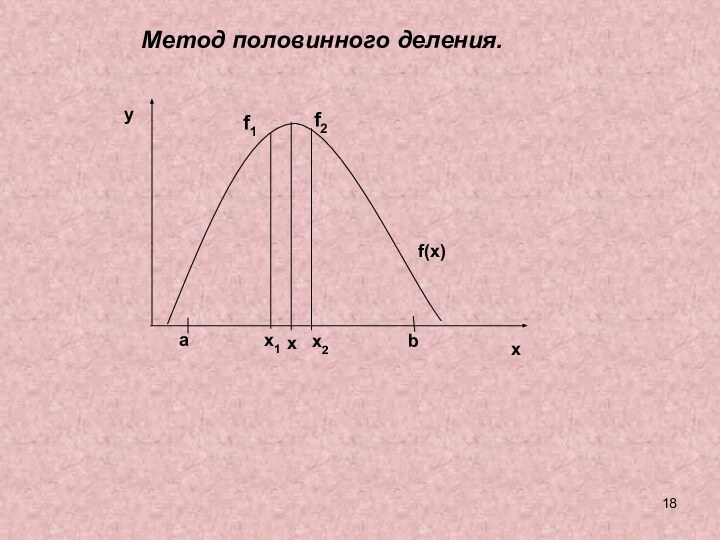
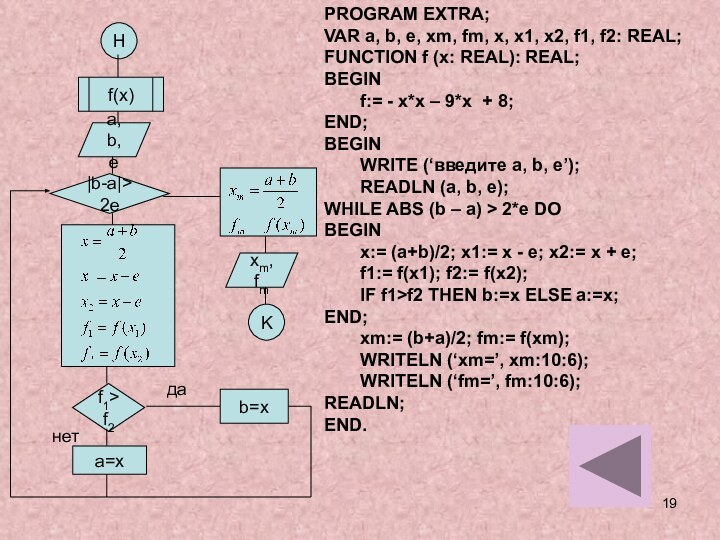
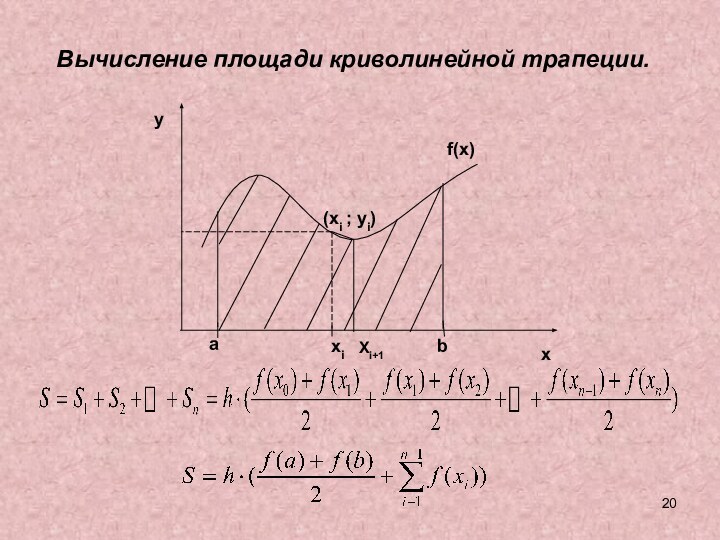
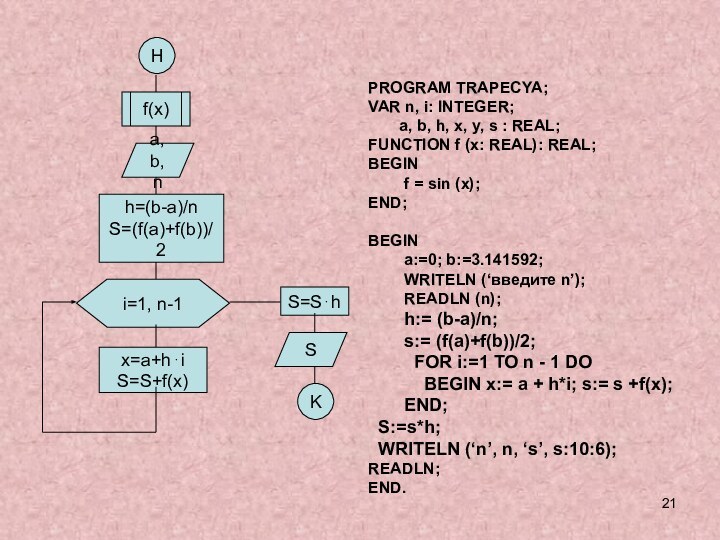
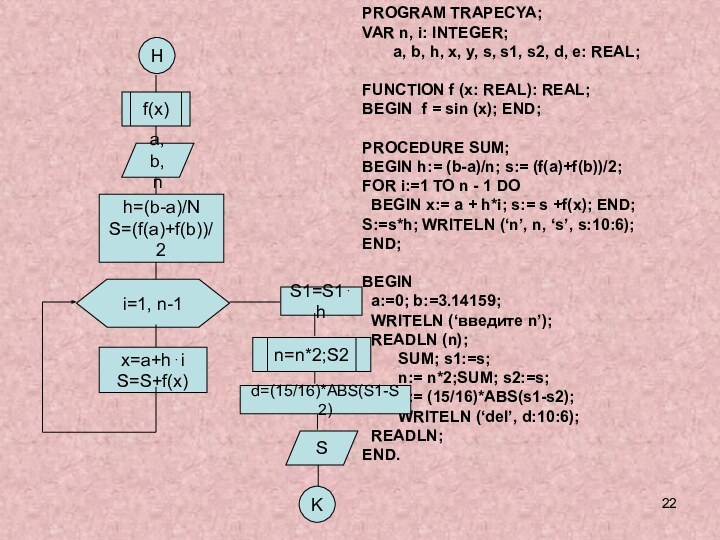
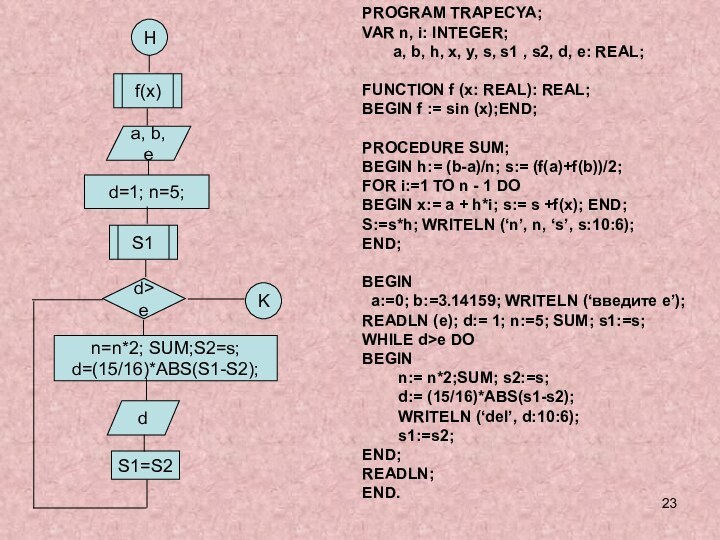
и исследовании моделей.

Модель – это некий новый объект, который

отражает существенные особенности изучаемого объекта, явления или процесса.

Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.

– замена натурального объекта его моделью

размещен в первом столбце (или строке) таблицы, а значения их свойств

размещаются в следующих столбцах (или строках) таблицы.

элемент более высокого уровня может состоять из элементов нижнего уровня, а

элемент нижнего уровня может входить в состав только одного элемента более высокого уровня.

Компьютеры

Суперкомпьютеры

Серверы

Персональные
компьютеры

Настольные

Портативные

Карманные

структурой, в которых связи между элементами имеют произвольный характер.

называются статическими информационными моделями.





Модели, описывающие процессы изменения и развития

систем, называются динамическими информационными моделями.

логические
и д.р.). Одним из наиболее широко используемых
формальных языков

является математика.

Формальные информационные модели

Математические модели

Логические модели

формул, уравнений, неравенств и т.д., отражающих существенные свойства
объекта

или явления.

описательной информационной модели.
Создание формализованной модели.
Преобразование формализованной модели в компьютерную

модель.
Проведение компьютерного эксперимента.
Анализ полученных результатов и коррекция исследуемой модели.

трапеции

e, p, x0: REAL;
FUNCTION f (x: REAL): REAL;
BEGIN
f:=cos(x)-x;
END;
BEGIN
WRITE

(‘Введите a, b, e’);
READLN (a, b, e);
WHILE ABS (b-a) > 2*e DO
BEGIN
c:= (a+b)/2;
p:= f(a)*f(с);
IF p>0 THEN a:=с ELSE b:=c;
END;
x0:= (a+b)/2;
WRITELN (‘x0=’, x0:10:6);
READLN;
END.

xm, fm, x, x1, x2, f1, f2: REAL;
FUNCTION f

(x: REAL): REAL;
BEGIN
f:= - x*x – 9*x + 8;
END;
BEGIN
WRITE (‘введите a, b, e’);
READLN (a, b, e);
WHILE ABS (b – a) > 2*e DO
BEGIN
x:= (a+b)/2; x1:= x - e; x2:= x + e;
f1:= f(x1); f2:= f(x2);
IF f1>f2 THEN b:=x ELSE a:=x;
END;
xm:= (b+a)/2; fm:= f(xm);
WRITELN (‘xm=’, xm:10:6);
WRITELN (‘fm=’, fm:10:6);
READLN;
END.

да

нет

a, b, h, x, y, s

: REAL;
FUNCTION f (x: REAL): REAL;
BEGIN
f = sin (x);
END;

BEGIN
a:=0; b:=3.141592;
WRITELN (‘введите n’);
READLN (n);
h:= (b-a)/n;
s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h;
WRITELN (‘n’, n, ‘s’, s:10:6);
READLN;
END.

a, b, h, x, y, s,

s1, s2, d, e: REAL;

FUNCTION f (x: REAL): REAL;
BEGIN f = sin (x); END;

PROCEDURE SUM;
BEGIN h:= (b-a)/n; s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h; WRITELN (‘n’, n, ‘s’, s:10:6);
END;

BEGIN
a:=0; b:=3.14159;
WRITELN (‘введите n’);
READLN (n);
SUM; s1:=s;
n:= n*2;SUM; s2:=s;
d:= (15/16)*ABS(s1-s2);
WRITELN (‘del’, d:10:6);
READLN;
END.

n=n*2;S2

d=(15/16)*ABS(S1-S2)

i: INTEGER;
a, b, h, x,

y, s, s1 , s2, d, e: REAL;

FUNCTION f (x: REAL): REAL;
BEGIN f := sin (x);END;

PROCEDURE SUM;
BEGIN h:= (b-a)/n; s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h; WRITELN (‘n’, n, ‘s’, s:10:6);
END;

BEGIN
a:=0; b:=3.14159; WRITELN (‘введите e’);
READLN (e); d:= 1; n:=5; SUM; s1:=s;
WHILE d>e DO
BEGIN
n:= n*2;SUM; s2:=s;
d:= (15/16)*ABS(s1-s2);
WRITELN (‘del’, d:10:6);
s1:=s2;
END;
READLN;
END.

S1

d>e