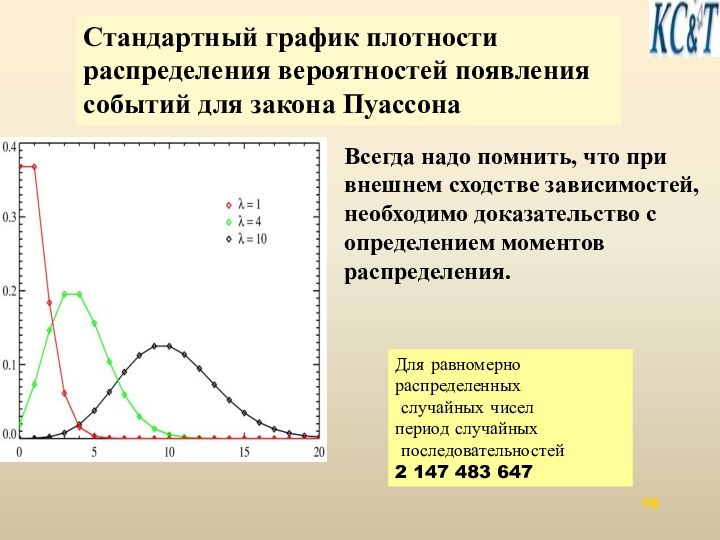
Описание потоков требований в
СМОТеорема о максимальном потоке
Максимальный поток равен минимальной пропускной способности по всем сечениям СМО.
Сечение - это множество каналов передачи требований, удаление которых приводит к разрыву всех возможных путей потоков от начальной до конечной точек пути.
СМО описывается марковскими процессами, в которых вероятность следующего значения Xn+1 зависит только от текущего состояния Xn и не зависит от предыдущих значений процесса. Формула m/m/1- означает, что поток требований и обработка их описываются марковскими процессами









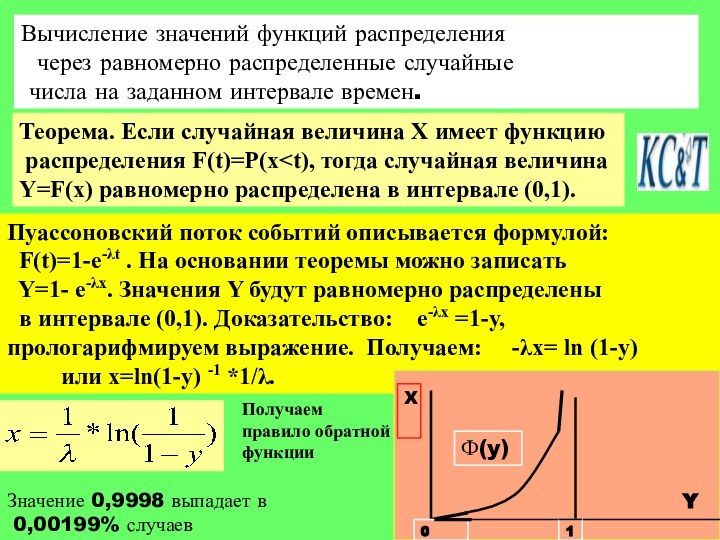

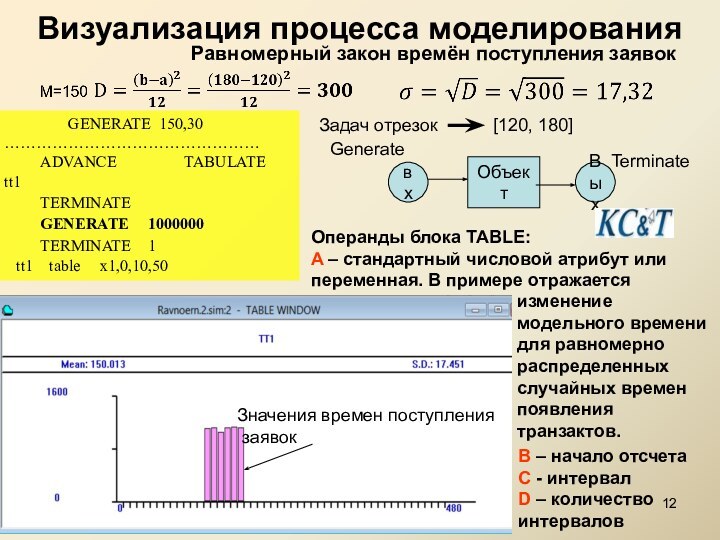

![Моделирование потоков заявок и функций распределения времен поступления и обработки заявок Моделирование экспоненциального распределениявремен поступления заявок для отрезка [120,180]В описании функции распределения времен](/img/tmb/15/1470007/f6e92b3e26680f451b558ff309ee5f86-720x.jpg)