Презентация на тему Моделирование. Решение популяционных задач

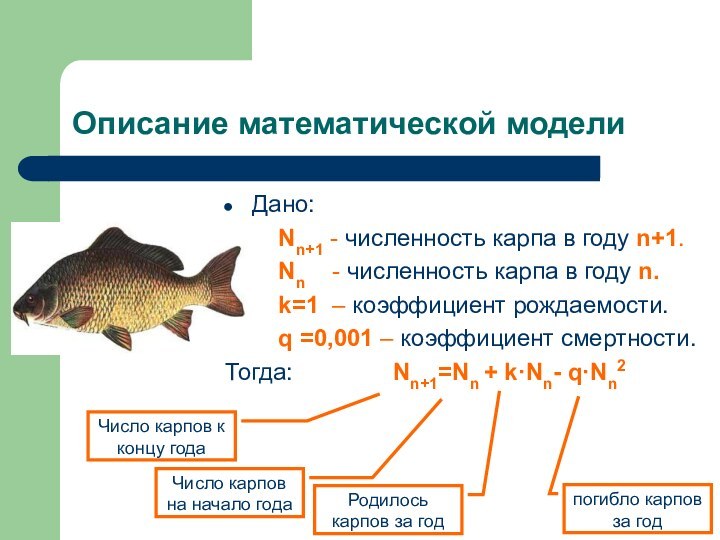
особей вида, входящая в состав биогеоценоза.
Популяционная динамика, - исследует

изменение численности популяции во времени.
Математическое моделирование помогает
формализовать знания об объекте,
дать описание процесса, предсказать его ход и эффективность,
дать рекомендации по управлению этим процессом.
Это крайне важно для биологических процессов, промышленного назначения - биотехнологических систем, продуктивность которых определяется ростом популяций живых организмов.

1798 г. в его работе "О росте народонаселения".


Где

- численность популяции в году n;
- численность в году n+1;
- коэффициент рождаемости.


Томас Роберт Мальтус (1766-1834) английский демограф и экономист.
Обнаружил, что численность популяций растет в геометрической прогрессии, а производство продуктов питания линейно (в арифметической прогрессии), из чего сделал вывод, что неизбежно наступит мировой голод.

Ферхюльст (1848) – в логистическом уравнении.

Это уравнение в дискретном

виде
Nn+1=Nn+kNn-qNn2
где Nn+1 численность популяции в году n+1;
Nn - численность популяции в году n;
k – коэффициент рождаемости;
q – коэффициент смертности.

важными свойствами:
при малых х численность х возрастает экспоненциально;

при больших х - приближается к определенному пределу К.
Величина К называется емкость популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования и многими другими факторами, которые могут быть разными для разных видов.

Динамика численности жука Rhizopertha dominica в 10-граммовой порции пшеничных зерен, пополняемых каждую неделю.

Динамика численности жука Rhizopertha dominica

возможность прогнозирования численности популяции обычными методами интерполяции.
Сделать выводы о

возможности применения этих методов в задачах о численности популяции.

Excel, не могут быть использованы для прогнозирования поведения модели

ограниченного роста популяции.

для разведения карпа.
Карпы питаются за счет ресурсов пруда.
Параметры

прудового хозяйства определены в рамках математической модели ограниченного роста популяции.

численность карпа в году n+1.
Nn

- численность карпа в году n.
k=1 – коэффициент рождаемости.
q =0,001 – коэффициент смертности.
Тогда: Nn+1=Nn + k·Nn- q·Nn2

Число карпов на начало года

Родилось карпов за год

погибло карпов за год

Число карпов к концу года

Nn+1 - численность карпа в году n+1;

Nn - численность карпа в году n;
k=1 – коэффициент рождаемости;
q =0,001 – коэффициент смертности;
U – ежегодный улов, заданный количеством особей

Тогда: Nn+1=Nn+k·Nn-q·Nn2-U

Число карпов на начало года

Родилось карпов за год

погибло карпов за год

Число карпов к концу года

отловлено карпов за год

после стабилизации популяции на уровне емкости популяции.
Определить с какого

года возможно отлавливать рыбу в максимальном размере.
Определить какое количество элитных мальков карпа надо запустить в пруд, чтобы начать отлов на максимальном уровне уже через год.
Определить через сколько лет окупятся затраты на приобретение элитных мальков. (Кредит 20% годовых)
Исследовать влияние коэффициента рождаемости на динамику популяции, дать своё обоснование каждому из полученных графиков.

«Название и автор».
2.Исследование возможности прогнозирования
3. Слайд «Математическая модель».
4.

Слайд «Реализация модели в Excel».
5-11. Слайды ответы на вопросы исследования.
12. Слайд «Направление дальнейших исследований».

улова (недолов)
Определение улова (перелов)
Определение улова (оптимально)

высоком коэффициенте рождаемости.

9-11 класс, Макарова Н.В., «Питер», 2008 год.
Избранные вопросы математического

моделирования и численных методов. Учебное пособие. Автор/создатель: Тарасевич Ю.Ю.,Год: 2004. (http://window.edu.ru/library/pdf2txt/936/38936/16634/page6).
Г.Ю.Ризниченко Популяционная динамика (http://www.library.biophys.msu.ru/MathMod/PD.HTML).
Видео ролик video.raid.ru/pages/video/58845/.
Динамика численности Lucilia cuprina http://www.slidefinder.net/l/lect_15_fert_human_pop_growth/32718196/p2.
festival.1september.ru/articles/571753/prez.ppt
kvlar.3dn.ru/dowl/dinamika_populiacii.ppt
http://www.metod-kopilka.ru/page-2-2-9-9.html