Слайд 3
Что такое флаттер?
Флаттер – это динамическая неустойчивость упругой
конструкции в потоке газа.
Неустойчивость конструкции проявляется в очень быстром
нарастании амплитуд колебаний, которое как правило приводит к разрушению элемента конструкции, подверженного флаттеру.
Каждый элемент упругой конструкции, обтекаемой потоком газа, совершает сложное колебательное движение. Эти движения часто не совпадают по фазе.
При неблагоприятном сдвиге фаз упругий элемент ЛА начинает получать из набегающего потока значительно большее количество энергии, чем то, которое рассеивается внутри элемента.
В результате амплитуды колебаний элемента быстро возрастают и в течение нескольких секунд наступает разрушение.
Слайд 4
Инженерный подход
К конструкции прикладывается искусственная нагрузка, вызывающая гармонические
колебания.
Система является стабильной, если энергия искусственной нагрузки рассеиватеся
в конструкции
Если конструкции сообщается большее количество энергии, чем может рассеится, то происходит флаттер
Слайд 5
Уравнение динамики
Уравнение динамики имеет вид
Из-за наличия волнового следа,
аэродинамическая нагрузка является зависимой от времени
Слайд 6
Аэродинамическая нагрузка при гармонических колебаниях
В случае установившихся
гармонических колебаний перемещения вычисляются:
Аэродинамическая нагрузка:
где
(следует помнить )
Слайд 7
Гармонические колебания
В случае установившейся гармонических колебаний уравнение динамики
имеет вид:
- матрица искусственной нагрузки, необходимой
для возбуждения гармонических колебаний.
Слайд 8
Работа искусственной нагрузки за один период времени Т
может быть выражена как
Пусть
.
Значить
что означает
Изменение энерии
Слайд 9
Уравнения флаттера
Уравнение флаттера имеет вид
Система устойчива если нет
действительных корней ω при
g > 0.
Флаттер получаем если
есть действительные корни ω при
g > 0.
Поиск области устойчивости, для каждого действительного корня существует значение g, которое является функцией от скорости.
Слайд 10
Обсуждение уравнения флаттера
Уравнение флаттера - нелинейная задача по
определению комплексных собственных значений.
Рассматриваются случаи, когда для комбинации параметров
ω, g, q, k и M существует нетривиальное решение Ua.
Однако, значения параметров должны соответствовать выражениям:
где V – скорость полета, h – высота.
Слайд 11
Точки согласования
Точки согласования – это такие комбинации скорости
полета V и высоты h, для которых
Справедливы вышеупомянутые уравнения
и
Существвует действительная ω, удовлетворяющая уравнению флаттера и
Для которой g = 0.
В диапазоне эксплуатационных режимов не должно существовать точек согласования.
Слайд 12
Модальное преобразование
По причине наибольшей эффективности, уравнение флаттера, после
решения, всегда преобразовывается в модальные координаты
Если требуется, то в
преобразованное уравнение могут быть введены дополнительные точки.
Слайд 13
Методы решения
В MSC.Nastran доступны четыре метода решения:
PK-метод –
вычисляются собственные значения и собственные вектора для значения скоростей,
определяемых пользователем.
PKNL-метод – похожий на PK-метод, но в этом расчете не используются все вариации плотности, чисел Маха и скорости. Расчет производится только для комбинаций параметров. Этот метод необходим для детального исследования точек флаттера.
K-метод – расчитываются собственные значения и собственные вектрора для заданной пользователем приведенной частоты.
KE-метод – более эффективный, чем K-метод, но в нем не учитывается вязкое демпфирование.
Слайд 14
K-метод: идея
В аэродинамический коэффициент входит эквивалентная масса :
Коэффициент
вязкого демпфирования вычисляется как
.
Следовательно, полученное уравнение эквивалентно исходному уравнению флаттера при g = 0 .
Слайд 15
K-метод: задача на собственные значения
Поделив на (1+ig) в
итоге получаем
где
Эта задача на собственные значения решается для
p при произвольных значениях M, k и ρ.
Слайд 16
K-метод: результаты вычисления
V и g могут быть получены
из p2:
Частота f может быть получена, если известны значения
V и k:
Слайд 17
K-метод: постпроцессинг
Построив график зависимости g от V можно
определить скорость при которой кривая g пересечет ось абсцисс,
значения g изменяются от отрицательных к положительным.
В конечном счете, этот метод позоляет проверить является ли высота h такой, что скорость V согласуется с заданными параметрами M и ρ.
Слайд 18
KE-метод
KE-метод – метод, аналогичный K-методу, но
Bhh не учитывается
Собственные вектора не вычисляются
Значения корней сортируются по скорости
Этот метод
лучше всего использовать когда нужен детальный анализ или если необходимо построить график V-g.
Слайд 19
PK-метод: идея
Действительная часть коэффициента аэродинамической жесткости содержит жесткость.
Мнимая
часть коэффициента аэродинамической жесткости содержит вязкое демпфирование.
Принимается g =
0.
Слайд 20
PK-метод: задача на собственные значения
где
Все матрицы в этой
задаче на собственные значения действительные.
Задача на собственные значения
решается для p при произвольных значениях M, V и ρ.
Для итераций необходимо согласование ω и k.
Слайд 21
PK-метод: результаты вычислений
ω и γ могут быть вычислены
из p.
Комплексный корень p:
Действительный корень p:
Слайд 22
PK-метод: постпроцессинг
График зависимости γ от V позволяет определить
скорость, при которой γ пересекает нуль, изменяя свои значения
с отрицательных на положительные.
Точка пересечения означает возможную скорость флаттера.
В заключение, этот метод позволяет проверить, является ли высота h, такой что скорость V, соответствует определенным значениям M и ρ.
Слайд 23
Демпфирование в задачах флаттера
K-метод учитывает все виды демпфирования.
KE-метод
учитывает только демпфирование конструкции :
GE в объекте MATi
PARAM,
G
Модальное демпфирование (TABDMP1) с PARAM, KDAMP, -1
PK-метод только вязкое демпфирование:
Демпфирующие элементы: VISC, CDAMPi
Прямой ввод матриц: B2GG, B2PP
Модальное демпфирование (TABDMP1) с PARAM, KDAMP, 1
Слайд 24
Решение задач на комплексные собственные значения
K-метод:
Могут быть использованы
все методы, реализованные в MSC.Nastran.
Для объекта EIGC из bulk
data необходимо выбрать в control command переменную CMETHOD.
Рекомендуется использовать метод Хезенберга (Hessenberg method).
KE-метод и PK-метод:
Используется метод Хезенберга.
Объект EIGC не требуется.
Слайд 25
Матричная интерполяция
Для обеспечения наибольшей эффективности, аэродинамические матрицы для
множества пар, заданных пользователем, (M, k) вычисляются заранее.
Эти (M,
k) пары определяются в объекте MKAEROi из bulk data.
В действительности матрицам необходима интерполяция.
В PK- и PKNL-методах не происходит интерполяции числа Маха.
Слайд 26
Объекты, задающие расчет флаттера
Объект FLUTTER из bulk data
entry:
Определяется метод расчета флаттера
Ссылается на множество объектов FLFACT
Если
выбран FMETHOD в case control command
Объект FLFACT из bulk data entries:
Для K- и KE-методов эти объекты определяют набор значений M, k и ρ.
Для PK- и PKNL-методов – набор значений M, V и ρ.
Слайд 27
Результаты расчета флаттера
Результаты:
Приведенная частота k и приведенная скорость
1/k
Плотность и число Маха
Скорость и демпфирование
Частоты и комплексные собственные
значения
Формы флаттера:
K-метод: DISPLACEMENT (перемещения), задается в case control command
PK- и PKNL-методы: DISPLACEMENT (перемещения), задается в case control command и отрицательная скорость в объекте FLFACT в bulk data entry
Графики:
Коэффициенты демпфирования и частоты, в зависимости от скорости
Слайд 28
Результаты вычислений
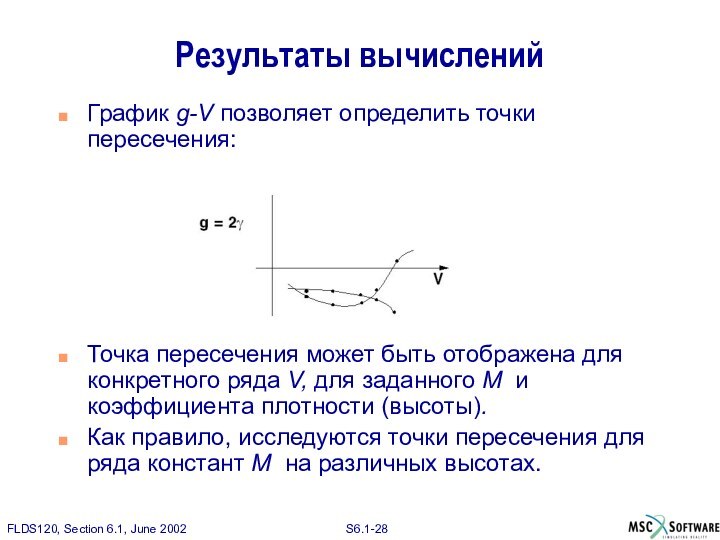
График g-V позволяет определить точки пересечения:
Точка пересечения
может быть отображена для конкретного ряда V, для заданного
M и коэффициента плотности (высоты).
Как правило, исследуются точки пересечения для ряда констант M на различных высотах.
Слайд 29
Поиск точек согласования
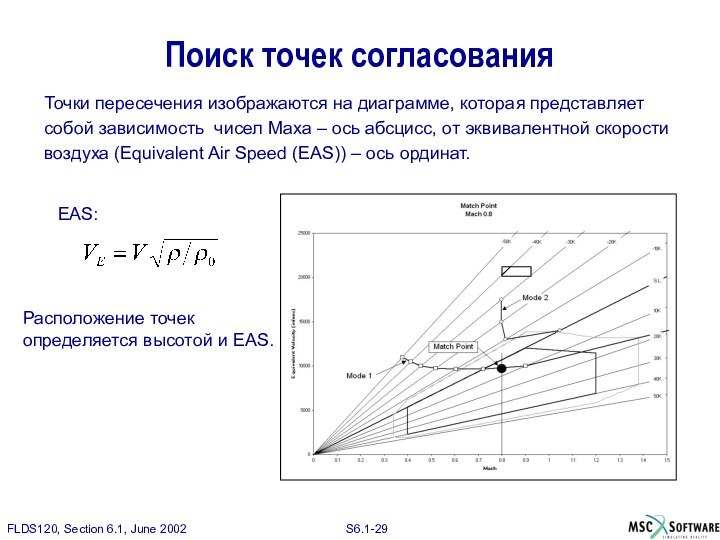
Точки пересечения изображаются на диаграмме, которая
представляет
собой зависимость чисел Маха – ось абсцисс, от эквивалентной
скорости
воздуха (Equivalent Air Speed (EAS)) – ось ординат.
EAS:
Расположение точек
определяется высотой и EAS.
Слайд 30
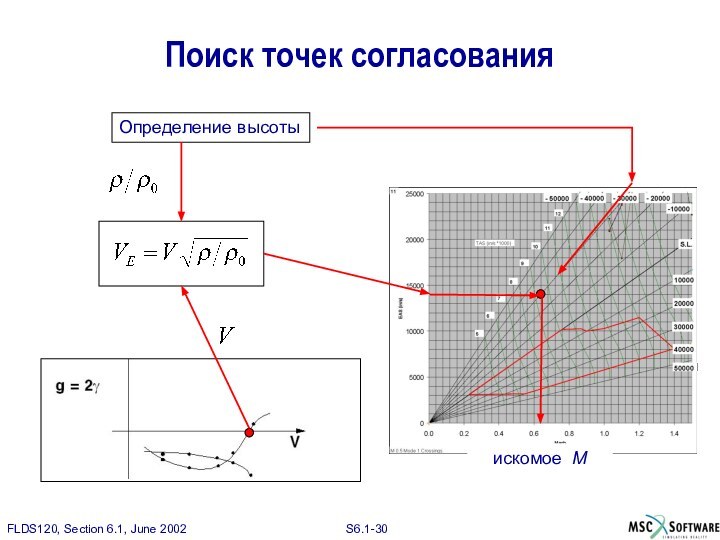
Поиск точек согласования
Определение высоты
искомое M
Слайд 31
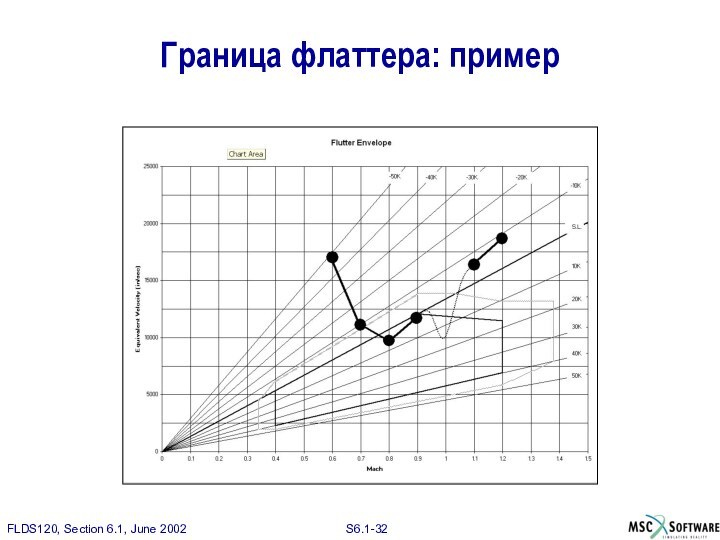
Граница флаттера
Множество точек согласования определяет границу флаттера.
Обычно рассматривается
15% запас в диапазоне эксплуатационных режимов
Слайд 33
Пример
На следующей странице представлен детальный пример расчета флаттера:
Отладка
модели
Оценка параметров флаттера
Стратегия исследования
Расчет
Интерпретация результатов
Используется модель TS1 – истребитель,
который использовался в статической аэроупругости.
Используется PK-метод.
Слайд 34
Отладка модели – собственные частоты
В начале мы проведем
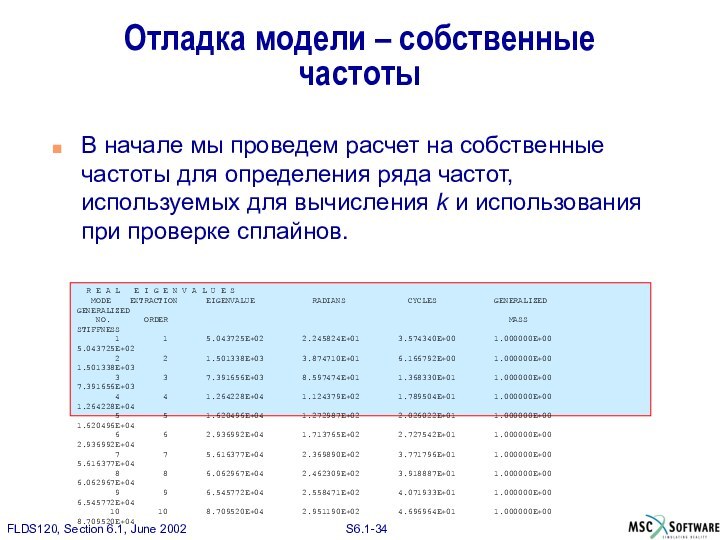
расчет на собственные частоты для определения ряда частот, используемых
для вычисления k и использования при проверке сплайнов.
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 5.043725E+02 2.245824E+01 3.574340E+00 1.000000E+00 5.043725E+02
2 2 1.501338E+03 3.874710E+01 6.166792E+00 1.000000E+00 1.501338E+03
3 3 7.391656E+03 8.597474E+01 1.368330E+01 1.000000E+00 7.391656E+03
4 4 1.264228E+04 1.124379E+02 1.789504E+01 1.000000E+00 1.264228E+04
5 5 1.620496E+04 1.272987E+02 2.026022E+01 1.000000E+00 1.620496E+04
6 6 2.936992E+04 1.713765E+02 2.727542E+01 1.000000E+00 2.936992E+04
7 7 5.616377E+04 2.369890E+02 3.771796E+01 1.000000E+00 5.616377E+04
8 8 6.062967E+04 2.462309E+02 3.918887E+01 1.000000E+00 6.062967E+04
9 9 6.545772E+04 2.558471E+02 4.071933E+01 1.000000E+00 6.545772E+04
10 10 8.709520E+04 2.951190E+02 4.696964E+01 1.000000E+00 8.709520E+04
Слайд 35
Отладка модели – расчет балансировки
Далее мы проведем расчет
статической аэроупругости для ряда значений числа Маха и высоты,
необходимый для проверки качества модели (смотри предыдущий раздел)
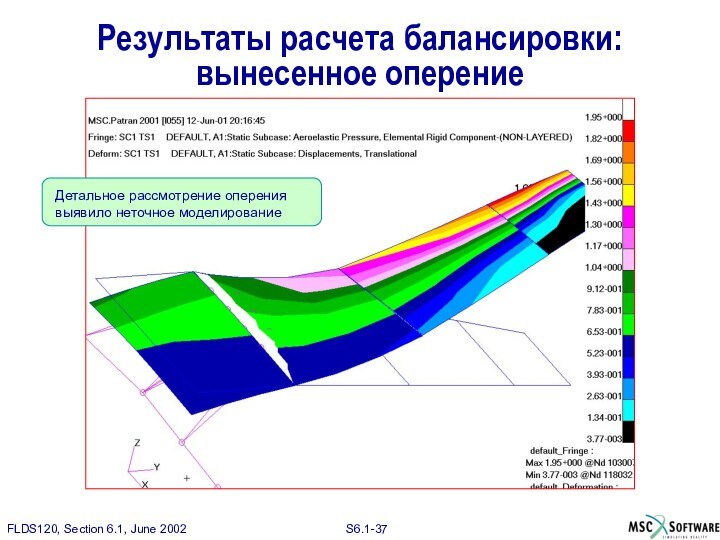
Результаты показывают, что в модели наблюдается отсутствие структурного определения сплайнов и «бедные» сплайны, расположенные на фюзеляжной части оперения.
Слайд 36
Результаты расчета балансировки
Распределение давления на «жеском» ЛА выглядит
нормально
Слайд 37
Результаты расчета балансировки: вынесенное оперение
Слайд 38
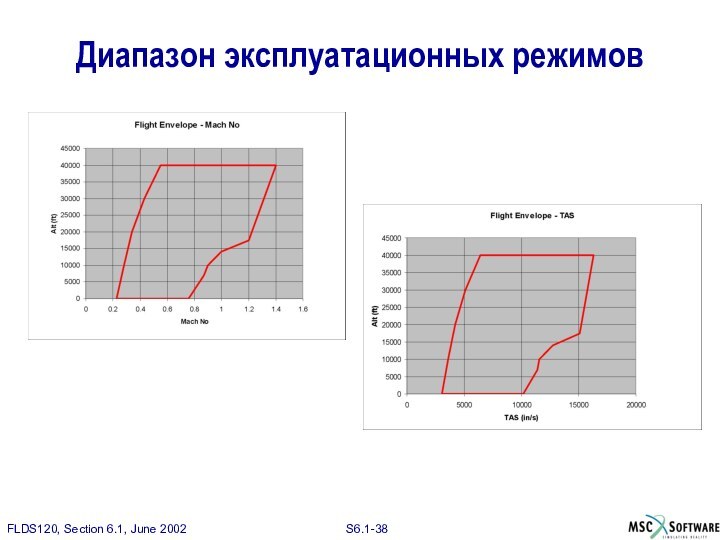
Диапазон эксплуатационных режимов
Слайд 39
Оценка ряда M, k и V
Исходя из данных
диапазона эксплуатационных параметров и собственных частот в неподвижном воздухе
мы можем оценить значения ряда чисел Маха, приведенной частоты и скорости
Скорости:
Минимальная скорость = 3080in/s (M = 0.23 на уровне моря)
Максимальная скорость = 16314in/s (M = 1.4 на высоте 40000ft)
Примечание: скорость требуется вводить в TAS (истинная скорость полета)
Частоты:
Минимальная частота = 3.57Hz ( 22.5rad/s)
Максимальная частота = 47.0Hz ( 295.1rad/s)
Длина хорды: c = 95in
Слайд 40
Проверка плотности аэродинамической сетки
Если эти параметры проверяются прямо
во FlightLoads, изображается картинка характеризующая параметр аэродинамических панелей к
длине волны (Aero Boxes per Wavelength) = V/f*c, где мы видим, что большая часть аэродинамической сетки не удовлетворяет критерию минимума = 15.
Это означает что расчет аэроупругости на этой части сетки будет давать неверные результаты
Следующая страница описывает как провести проверку в FlightLoads.
Слайд 41
Проверка плотности аэродинамической сетки
Слайд 42
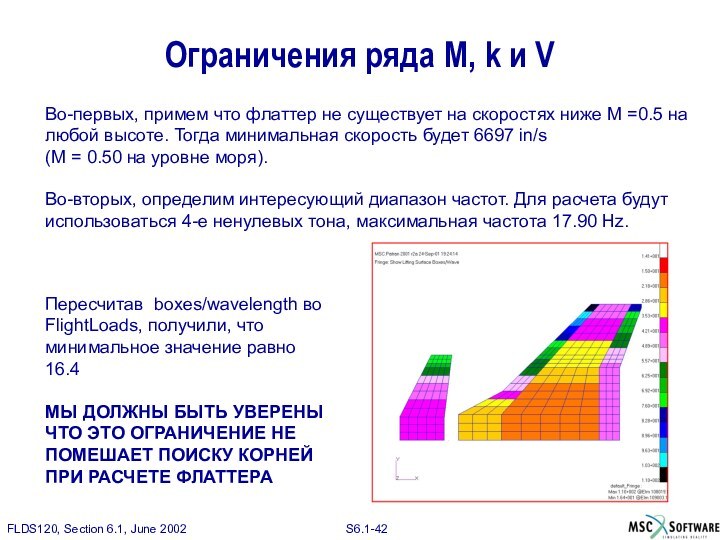
Ограничения ряда M, k и V
Во-первых, примем что
флаттер не существует на скоростях ниже M =0.5 на
любой высоте. Тогда минимальная скорость будет 6697 in/s
(M = 0.50 на уровне моря).
Во-вторых, определим интересующий диапазон частот. Для расчета будут использоваться 4-е ненулевых тона, максимальная частота 17.90 Hz.
Пересчитав boxes/wavelength во FlightLoads, получили, что минимальное значение равно 16.4
МЫ ДОЛЖНЫ БЫТЬ УВЕРЕНЫ ЧТО ЭТО ОГРАНИЧЕНИЕ НЕ ПОМЕШАЕТ ПОИСКУ КОРНЕЙ ПРИ РАСЧЕТЕ ФЛАТТЕРА
Слайд 43
Стратегия исследования
Эффективным путем поиска диапазона эксплуатационных режимов для
точек флаттера является полет при одном значении числа Маха
на различной высоте.
Из этого вытекает, что нужно задать множество пар (M, k) и ряд различных скоростей для каждой исследуемой области.
Рассмотрим исследуемые области:
Search 1: M = 0.5, 0.6, 0.7
Search 2: M = 0.8, 0.9, 0.97
Search 3: M = 1.03, 1.1, 1.2, 1.3, 1.4, 1.5
Слайд 44
Стратегия исследования
Для каждой исследуемой области выполняется один расчет.
В качестве альтернативы мы можем в одном расчете объединить
все исследуемые области.
Преимущество множественного расчета заключается в том что мы можем получить выигрыш при дальнейшем расчете, т.е. используя полученные значения V и k мы можем прогнозировать область следующего исследования.
В нашем случае, при первом расчете мы будем рассматривать значения чесел Маха от 0.5 до 0.7 и высоты от 50,000 ft до –50,000 ft с шагом 10000 ft.
Использование отрицательной высоты может показаться странной идеей, но с точки зрения математики эти коэффициенты плотности правомерны. Эти значения дополняют значения реальной картины и позволяют нам определить все границы.
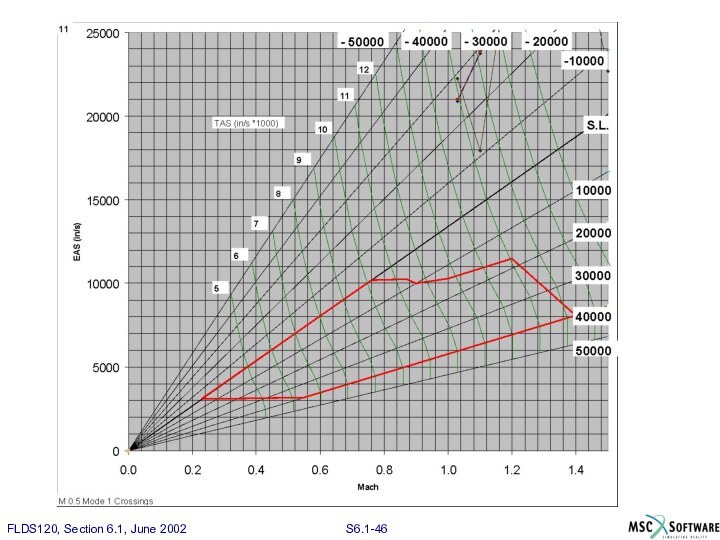
Слайд 45
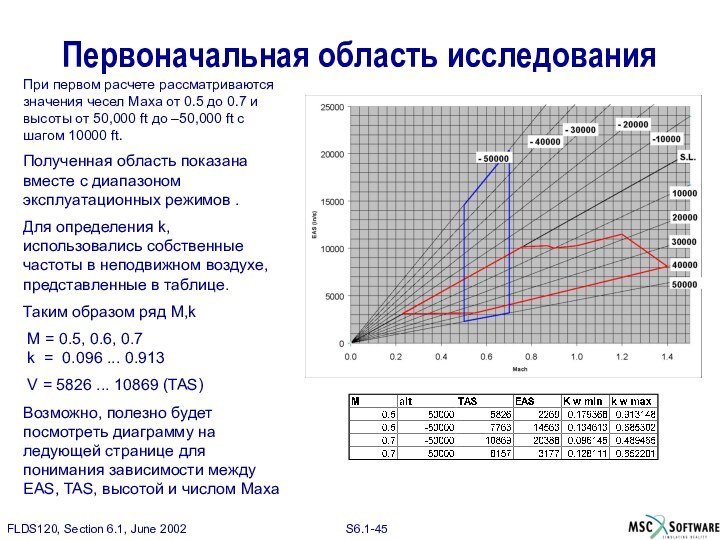
Первоначальная область исследования
При первом расчете рассматриваются значения чесел
Маха от 0.5 до 0.7 и высоты от 50,000
ft до –50,000 ft с шагом 10000 ft.
Полученная область показана вместе с диапазоном эксплуатационных режимов .
Для определения k, использовались собственные частоты в неподвижном воздухе, представленные в таблице.
Таким образом ряд M,k
M = 0.5, 0.6, 0.7
k = 0.096 ... 0.913
V = 5826 ... 10869 (TAS)
Возможно, полезно будет посмотреть диаграмму на ледующей странице для понимания зависимости между EAS, TAS, высотой и числом Маха
Слайд 47
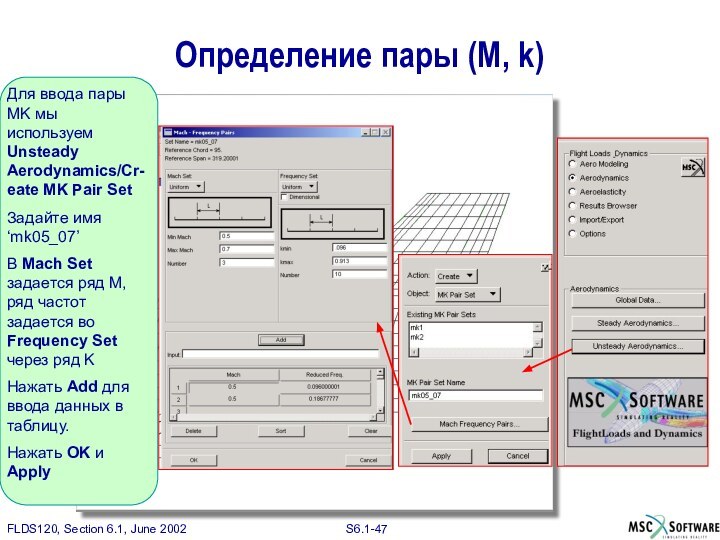
Для ввода пары MK мы используем Unsteady Aerodynamics/Cr-eate
MK Pair Set
Задайте имя ‘mk05_07’
В Mach Set задается ряд
М, ряд частот задается во Frequency Set через ряд K
Нажать Add для ввода данных в таблицу.
Нажать OK и Apply
Определение пары (M, k)
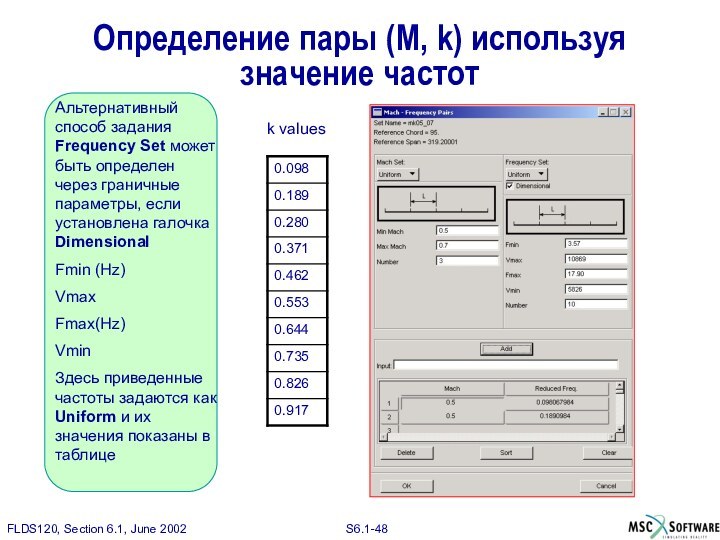
Слайд 48
Альтернативный способ задания Frequency Set может быть определен
через граничные параметры, если установлена галочка Dimensional
Fmin (Hz)
Vmax
Fmax(Hz)
Vmin
Здесь
приведенные частоты задаются как Uniform и их значения показаны в таблице
k values
Определение пары (M, k) используя значение частот
Слайд 49
k values
Для задани приведенных частот можно выбрать способ
Two Way Bias полученные значения приведены в таблице.
L1/L2 =
0.5 определяет концентрацию значений ряда относительно центра
Для расчетного случая мы будем использовать эти данные.
Определение «смещенных» приведенных частот
Слайд 50
Расчет флаттера для первой области исследований
Мы создадим расчетный
случай для каждого значения числа Маха : 0.5, 0.6
и 0.7
В настоящее время не все данные могут быть без труда установлены через графический интерфейс FlightLoads , исключая случая использования большого числа расчетных случаев.
Поэтому, для облегчения себе жизни, мы будем вручную править выходной .bdf файл FlightLoads Допустим, что аэродинамические плоскости и сплайны были созданы до расчена на статическую аэроупругость.
В этом расчетном случае мы будем повторно использовать данные из базы данных FLDS .
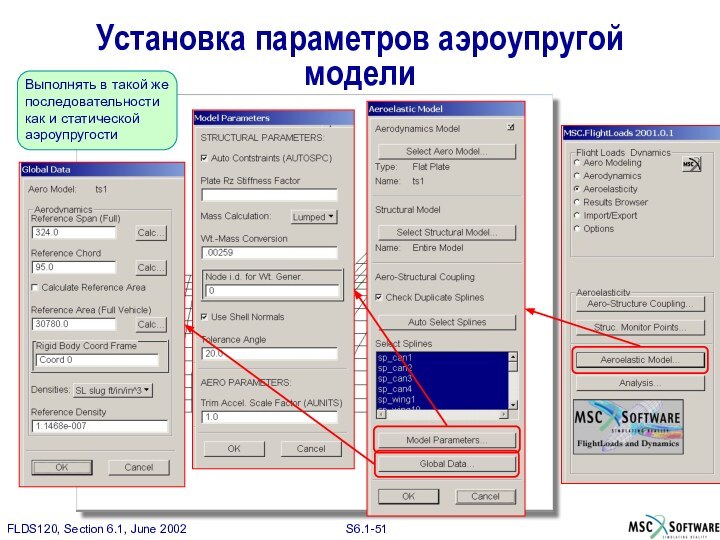
Слайд 51
Выполнять в такой же последовательности как и статической
аэроупругости
Установка параметров аэроупругой модели
Слайд 52
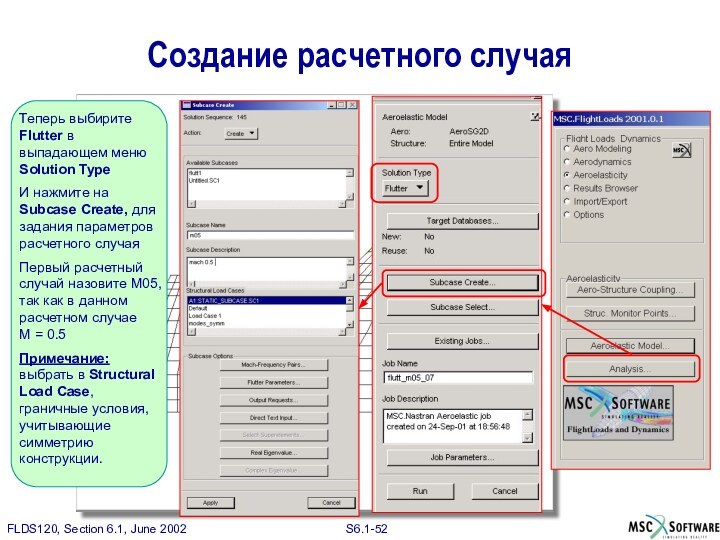
Теперь выбирите Flutter в выпадающем меню Solution Type
И
нажмите на Subcase Create, для задания параметров расчетного случая
Первый
расчетный случай назовите M05, так как в данном расчетном случае M = 0.5
Примечание: выбрать в Structural Load Case, граничные условия, учитывающие симметрию конструкции.
Создание расчетного случая
Слайд 53
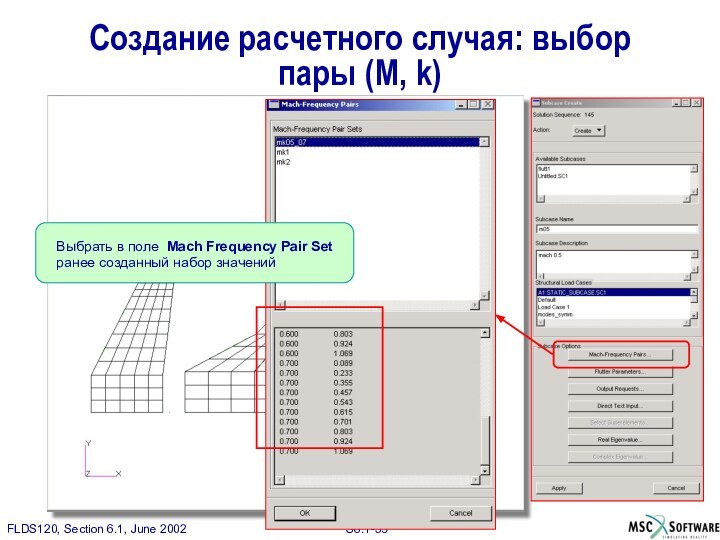
Выбрать в поле Mach Frequency Pair Set ранее
созданный набор значений
Создание расчетного случая: выбор пары (M, k)
Слайд 54
Создание расчетного случая: параметры расчета на флаттер
Слайд 55
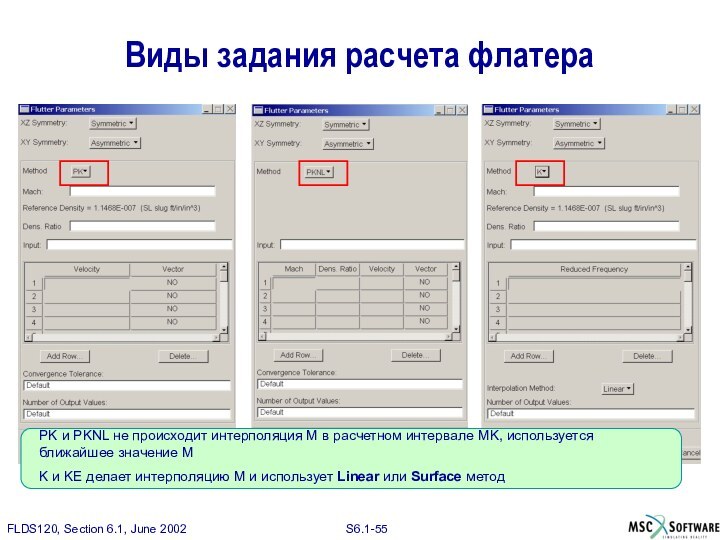
PK и PKNL не происходит интерполяция M в
расчетном интервале MK, используется ближайшее значение M
K и
KE делает интерполяцию M и использует Linear или Surface метод
Виды задания расчета флатера
Слайд 56
Выбор скоростей
Диапазон эксплуатационных режимов показывает что наименьшее значение
TAS получается на высоте –50,000ft при M = 0.5
и скорости 7763in/s.
Зхначения k-ряда от 0.089 ... 1.069. Соответствующий ряд скоростей от 1000in/s до 60,000in/s.
Рассмотрим ряд скоростей от 2000in/s до 15,000in/s с шагом 1000in/s.
Слайд 57
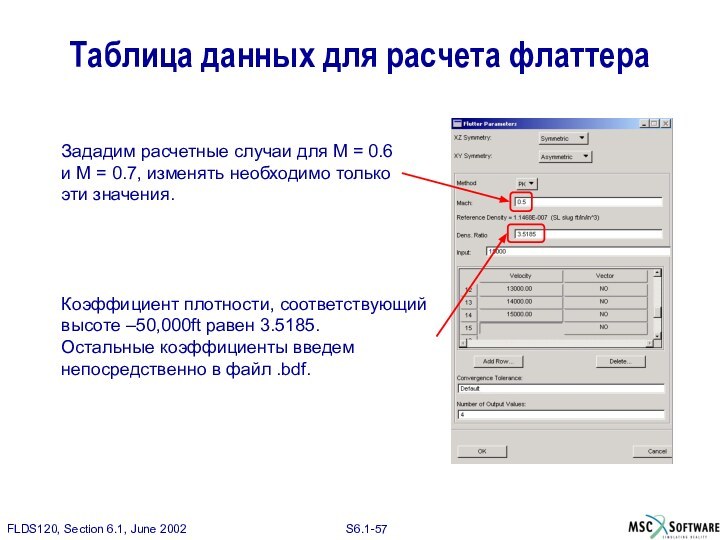
Таблица данных для расчета флаттера
Коэффициент плотности, соответствующий
высоте –50,000ft
равен 3.5185.
Остальные коэффициенты введем
непосредственно в файл .bdf.
Зададим расчетные
случаи для M = 0.6
и M = 0.7, изменять необходимо только
эти значения.
Слайд 58
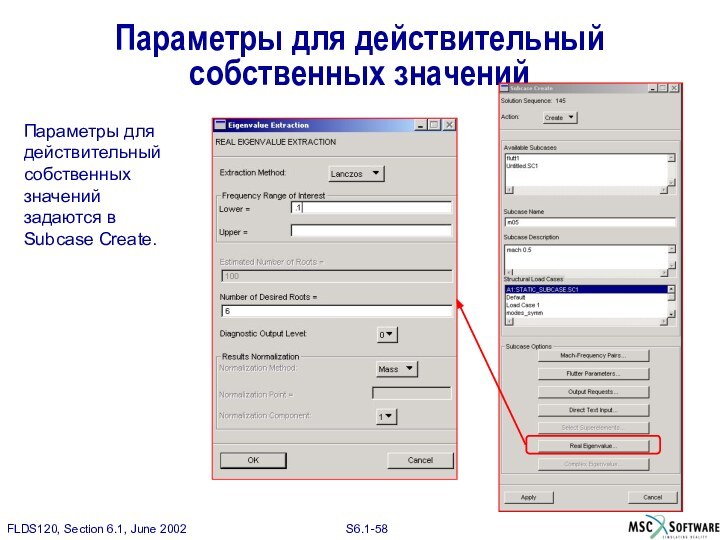
Параметры для действительный собственных значений
Параметры для действительный собственных
значений задаются в Subcase Creatе.
Слайд 59
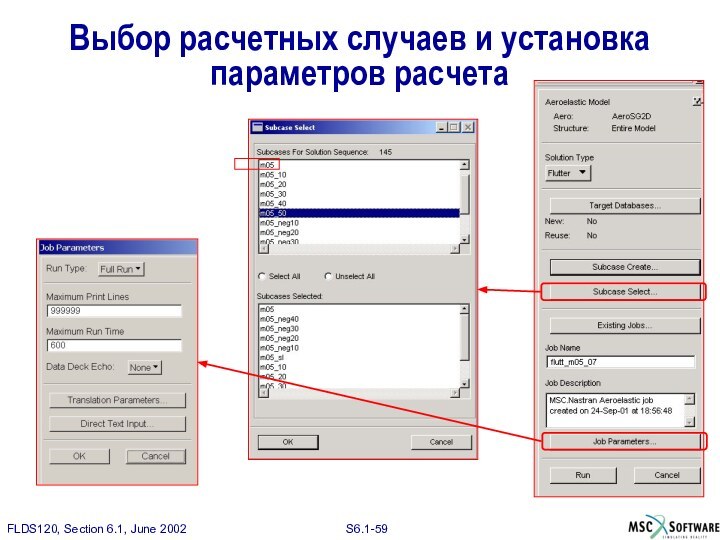
Выбор расчетных случаев и установка параметров расчета
Слайд 60
SOL 145
CEND
SEALL = ALL
SUPER = ALL
TITLE = MSC.Nastran
Aeroelastic job created on 25-Sep-01 at 15:25:36
ECHO = NONE
MAXLINES
= 999999
AECONFIG = AeroSG2D
SUBCASE 1
$ Subcase name : m05
SUBTITLE=A1:STATIC_SUBCASE.SC1
METHOD = 1
SPC = 2
VECTOR(SORT1,REAL)=ALL
SPCFORCES(SORT1,REAL)=ALL
FMETHOD = 1
AESYMXZ = Symmetric
AESYMXY = Asymmetric
SUBCASE 2
$ Subcase name : m06
SUBTITLE=A1:STATIC_SUBCASE.SC1
METHOD = 1
SPC = 2
VECTOR(SORT1,REAL)=ALL
SPCFORCES(SORT1,REAL)=ALL
FMETHOD = 2
AESYMXZ = Symmetric
AESYMXY = Asymmetric
SUBCASE 3
$ Subcase name : m07
SUBTITLE=A1:STATIC_SUBCASE.SC1
METHOD = 1
SPC = 2
VECTOR(SORT1,REAL)=ALL
SPCFORCES(SORT1,REAL)=ALL
FMETHOD = 3
AESYMXZ = Symmetric
AESYMXY = Asymmetric
Как вы видите в Case Control определены три расчетных случая.
Каждый управляется картой FMETHOD
Исполняемые команды и команды для Case Control
Слайд 61
$ MKAERO2 card
$
$ Mach-Frequency Pair .MRG_MK_7
MKAERO2 .5
.088825 .5 .233266 .5
.354726 .5 .456861
MKAERO2 .5 .542746 .5 .614966 .5 .700851 .5 .802986
MKAERO2 .5 .924446 .5 1.068887.6 .088825 .6 .233266
MKAERO2 .6 .354726 .6 .456861 .6 .542746 .6 .614966
MKAERO2 .6 .700851 .6 .802986 .6 .924446 .6 1.068887
MKAERO2 .7 .088825 .7 .233266 .7 .354726 .7 .456861
MKAERO2 .7 .542746 .7 .614966 .7 .700851 .7 .802986
MKAERO2 .7 .924446 .7 1.068887
$
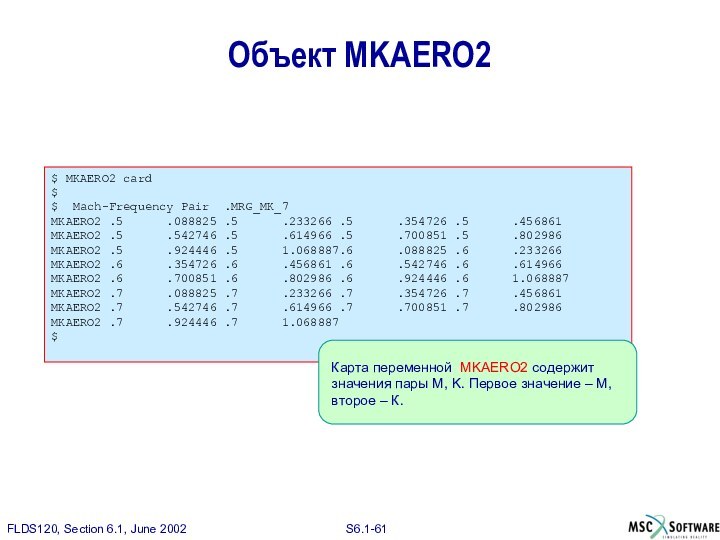
Карта переменной MKAERO2 содержит значения пары M, K. Первое значение – М, второе – К.
Объект MKAERO2
Слайд 62
$
$ Density Ratios
FLFACT 34 3.5185
$
$
Mach number sets
FLFACT 35 .5
$
$ Velocity sets
FLFACT
36 2000. 3000. 4000. 5000. 6000. 7000. 8000.
9000. 10000. 11000. 12000. 13000. 14000. 15000.
FLUTTER 1 PK 34 35 36 4 .001
$
$ Density Ratios
FLFACT 37 3.5185
$
$ Mach number sets
FLFACT 38 .6
$
$ Velocity sets
FLFACT 39 2000. 3000. 4000. 5000. 6000. 7000. 8000.
9000. 10000. 11000. 12000. 13000. 14000. 15000.
FLUTTER 2 PK 37 38 39 4 .001
$
$ Density Ratios
FLFACT 40 3.5185
$
$ Mach number sets
FLFACT 41 .7
$
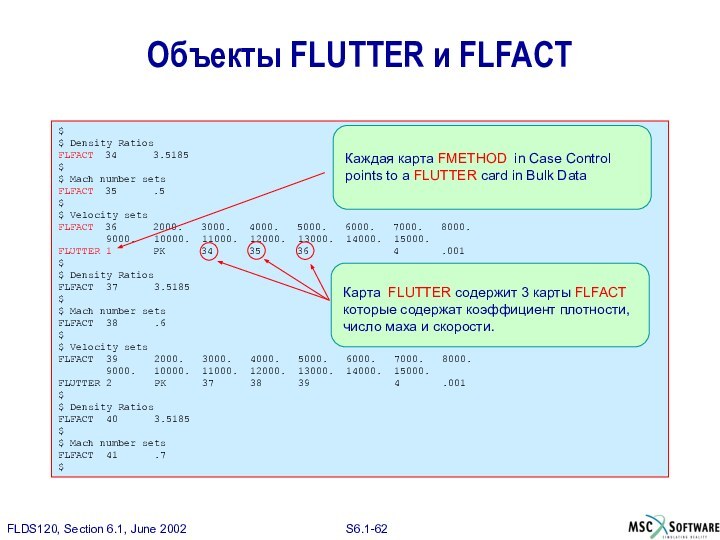
Каждая карта FMETHOD in Case Control points to a FLUTTER card in Bulk Data
Карта FLUTTER содержит 3 карты FLFACT которые содержат коэффициент плотности, число маха и скорости.
Объекты FLUTTER и FLFACT
Слайд 63
$
$ Density Ratios
FLFACT 34 3.5185 2.8135
2.2220 1.7308 1.3273 1.0 0.7384
0.5326 0.3739 0.2446 0.1517
$
$ Mach number sets
FLFACT 35 .5
$
$ Velocity sets
FLFACT 36 2000. 3000. 4000. 5000. 6000. 7000. 8000.
9000. 10000. 11000. 12000. 13000. 14000. 15000.
FLUTTER 1 PK 34 35 36 4 .001
$
$ Density Ratios
FLFACT 37 3.5185 2.8135 2.2220 1.7308 1.3273 1.0 0.7384
0.5326 0.3739 0.2446 0.1517
$
$ Mach number sets
FLFACT 38 .6
$
$ Velocity sets
FLFACT 39 2000. 3000. 4000. 5000. 6000. 7000. 8000.
9000. 10000. 11000. 12000. 13000. 14000. 15000.
FLUTTER 2 PK 37 38 39 4 .001
$
$ Density Ratios
FLFACT 40 3.5185 2.8135 2.2220 1.7308 1.3273 1.0 0.7384
0.5326 0.3739 0.2446 0.1517
$
Карта FLFACT может также содержать и список значений плотности.
Внимание: проверте правильность ваших коэффициентов на соответствие параметрам атмосферы, данные значения приведены в качесве примера.
Редактирование коэффициентов плотности
Слайд 64
Результаты
На следующей странице обсуждаются результаты, выводимые в файл
.f06.
Графики V-g и V-f могут быть получены с помощью
функций Nastran.
Альтернативный метод предусматривает создание файла .pch для постпроцессинга в ином програмном обеспечении.
Значения комплексных собственных векторов для полученных корней уравнения флаттера могут быть записаны в файл .xdb. В Patran можно произвести анимацию этих векторов на соответствующих отрицательных скоростях.
Слайд 65
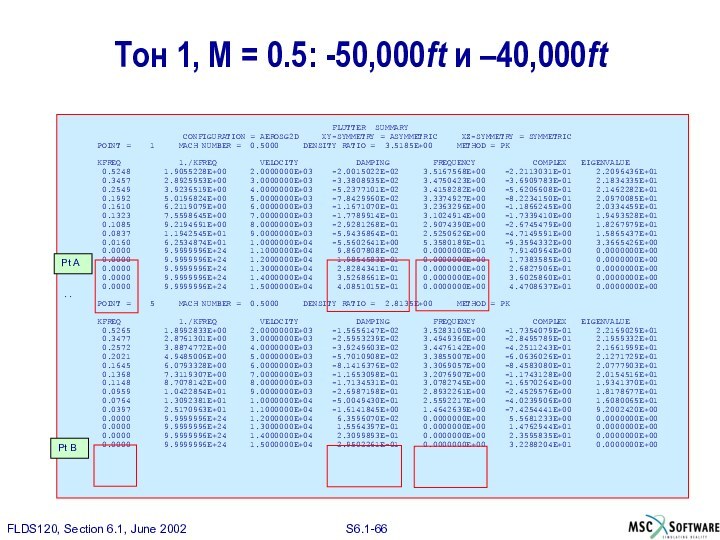
Результаты представленные в файле .f06
Ниже представлены результаты полученые
при M = 0.5 и изменении высоты от –50000ft
до -10000ft, для первого тона. При этом числе Маха не были найдены точки пересечения, соответствующие высоте равной уровню моря
Результаты, аналогичные, полученным для первого тона, были получены и для всего исследуемого ряда (M = 0.5 ... M = 0.7).
Точки пересечения выделены и обозначены как Point A ... Point E.
Для второго тона тоже были найдены точки пересечения, но они не представлены здесь.
FLUTTER SUMMARY
CONFIGURATION = AEROSG2D XY-SYMMETRY = ASYMMETRIC XZ-SYMMETRY = SYMMETRIC
POINT = 1 MACH NUMBER = 0.5000 DENSITY RATIO = 3.5185E+00 METHOD = PK
KFREQ 1./KFREQ VELOCITY DAMPING FREQUENCY COMPLEX EIGENVALUE
0.5248 1.9055228E+00 2.0000000E+03 -2.0015022E-02 3.5167568E+00 -2.2113031E-01 2.2096436E+01
0.3457 2.8925953E+00 3.0000000E+03 -3.3808935E-02 3.4750423E+00 -3.6909783E-01 2.1834335E+01
0.2549 3.9236519E+00 4.0000000E+03 -5.2377101E-02 3.4158282E+00 -5.6206608E-01 2.1462282E+01
0.1992 5.0196824E+00 5.0000000E+03 -7.8429960E-02 3.3374927E+00 -8.2234150E-01 2.0970085E+01
0.1610 6.2119079E+00 6.0000000E+03 -1.1671070E-01 3.2363296E+00 -1.1866245E+00 2.0334459E+01
0.1323 7.5598645E+00 7.0000000E+03 -1.7789914E-01 3.1024914E+00 -1.7339410E+00 1.9493528E+01
0.1085 9.2194691E+00 8.0000000E+03 -2.9281268E-01 2.9074390E+00 -2.6745479E+00 1.8267979E+01
0.0837 1.1942545E+01 9.0000000E+03 -5.9436864E-01 2.5250626E+00 -4.7149591E+00 1.5865437E+01
0.0160 6.2534874E+01 1.0000000E+04 -5.5602641E+00 5.3580189E-01 -9.3594332E+00 3.3665426E+00
0.0000 9.9999996E+24 1.1000000E+04 9.8607808E-02 0.0000000E+00 7.9140964E+00 0.0000000E+00
0.0000 9.9999996E+24 1.2000000E+04 1.9854583E-01 0.0000000E+00 1.7383585E+01 0.0000000E+00
0.0000 9.9999996E+24 1.3000000E+04 2.8284341E-01 0.0000000E+00 2.6827906E+01 0.0000000E+00
0.0000 9.9999996E+24 1.4000000E+04 3.5268661E-01 0.0000000E+00 3.6025860E+01 0.0000000E+00
0.0000 9.9999996E+24 1.5000000E+04 4.0851015E-01 0.0000000E+00 4.4708637E+01 0.0000000E+00
..
POINT = 5 MACH NUMBER = 0.5000 DENSITY RATIO = 2.8135E+00 METHOD = PK
KFREQ 1./KFREQ VELOCITY DAMPING FREQUENCY COMPLEX EIGENVALUE
0.5265 1.8992833E+00 2.0000000E+03 -1.5656147E-02 3.5283105E+00 -1.7354079E-01 2.2169029E+01
0.3477 2.8761301E+00 3.0000000E+03 -2.5953239E-02 3.4949360E+00 -2.8495789E-01 2.1959332E+01
0.2572 3.8874772E+00 4.0000000E+03 -3.9249603E-02 3.4476142E+00 -4.2511243E-01 2.1661999E+01
0.2021 4.9485006E+00 5.0000000E+03 -5.7010908E-02 3.3855007E+00 -6.0636026E-01 2.1271729E+01
0.1645 6.0793328E+00 6.0000000E+03 -8.1416376E-02 3.3069057E+00 -8.4583080E-01 2.0777903E+01
0.1368 7.3119307E+00 7.0000000E+03 -1.1653098E-01 3.2076907E+00 -1.1743128E+00 2.0154516E+01
0.1148 8.7078142E+00 8.0000000E+03 -1.7134531E-01 3.0782745E+00 -1.6570264E+00 1.9341370E+01
0.0959 1.0422854E+01 9.0000000E+03 -2.6987198E-01 2.8932261E+00 -2.4529576E+00 1.8178677E+01
0.0764 1.3092381E+01 1.0000000E+04 -5.0049430E-01 2.5592217E+00 -4.0239906E+00 1.6080065E+01
0.0397 2.5170963E+01 1.1000000E+04 -1.6141845E+00 1.4642639E+00 -7.4254441E+00 9.2002420E+00
0.0000 9.9999996E+24 1.2000000E+04 6.3596070E-02 0.0000000E+00 5.5681233E+00 0.0000000E+00
0.0000 9.9999996E+24 1.3000000E+04 1.5564397E-01 0.0000000E+00 1.4762944E+01 0.0000000E+00
0.0000 9.9999996E+24 1.4000000E+04 2.3099893E-01 0.0000000E+00 2.3595835E+01 0.0000000E+00
0.0000 9.9999996E+24 1.5000000E+04 2.9502261E-01 0.0000000E+00 3.2288204E+01 0.0000000E+00
Тон 1, M = 0.5: -50,000ft и –40,000ft
Pt A
Pt B
Слайд 67
Тон 1, M = 0.5: -30,000ft и –20,000ft
.....

POINT = 9 MACH NUMBER =
0.5000 DENSITY RATIO = 2.2220E+00 METHOD = PK
KFREQ 1./KFREQ VELOCITY DAMPING FREQUENCY COMPLEX EIGENVALUE
0.5280 1.8940805E+00 2.0000000E+03 -1.2134661E-02 3.5380020E+00 -1.3487630E-01 2.2229923E+01
0.3494 2.8624496E+00 3.0000000E+03 -1.9787800E-02 3.5116396E+00 -2.1830180E-01 2.2064283E+01
0.2592 3.8576853E+00 4.0000000E+03 -2.9299384E-02 3.4742391E+00 -3.1979236E-01 2.1829288E+01
0.2045 4.8907447E+00 5.0000000E+03 -4.1477069E-02 3.4254808E+00 -4.4635406E-01 2.1522932E+01
0.1674 5.9752741E+00 6.0000000E+03 -5.7352629E-02 3.3644955E+00 -6.0621011E-01 2.1139750E+01
0.1403 7.1300001E+00 7.0000000E+03 -7.8594670E-02 3.2895389E+00 -8.1222808E-01 2.0668783E+01
0.1193 8.3846073E+00 8.0000000E+03 -1.0829032E-01 3.1969349E+00 -1.0876104E+00 2.0086935E+01
0.1021 9.7943335E+00 9.0000000E+03 -1.5276782E-01 3.0788898E+00 -1.4776648E+00 1.9345236E+01
0.0871 1.1486335E+01 1.0000000E+04 -2.2715050E-01 2.9170580E+00 -2.0816545E+00 1.8328417E+01
0.0721 1.3869401E+01 1.1000000E+04 -3.7700710E-01 2.6574280E+00 -3.1474650E+00 1.6697113E+01
0.0514 1.9460722E+01 1.2000000E+04 -8.1357807E-01 2.0660880E+00 -5.2807784E+00 1.2981614E+01
0.0000 9.9999996E+24 1.3000000E+04 2.3165774E-03 0.0000000E+00 2.1972905E-01 0.0000000E+00
0.0000 9.9999996E+24 1.4000000E+04 1.0236141E-01 0.0000000E+00 1.0455905E+01 0.0000000E+00
0.0000 9.9999996E+24 1.5000000E+04 1.7129967E-01 0.0000000E+00 1.8747576E+01 0.0000000E+00
.....
POINT = 13 MACH NUMBER = 0.5000 DENSITY RATIO = 1.7308E+00 METHOD = PK
KFREQ 1./KFREQ VELOCITY DAMPING FREQUENCY COMPLEX EIGENVALUE
0.5292 1.8897933E+00 2.0000000E+03 -9.3038883E-03 3.5460286E+00 -1.0364697E-01 2.2280355E+01
0.3507 2.8511844E+00 3.0000000E+03 -1.4958534E-02 3.5255141E+00 -1.6567668E-01 2.2151459E+01
0.2609 3.8332427E+00 4.0000000E+03 -2.1747116E-02 3.4963925E+00 -2.3887558E-01 2.1968483E+01
0.2064 4.8440061E+00 5.0000000E+03 -3.0113488E-02 3.4585323E+00 -3.2719210E-01 2.1730600E+01
0.1697 5.8928776E+00 6.0000000E+03 -4.0556781E-02 3.4115388E+00 -4.3467402E-01 2.1435331E+01
0.1430 6.9915576E+00 7.0000000E+03 -5.3794511E-02 3.3546765E+00 -5.6694180E-01 2.1078054E+01
0.1226 8.1561832E+00 8.0000000E+03 -7.0996225E-02 3.2864690E+00 -7.3301810E-01 2.0649494E+01
0.1063 9.4115114E+00 9.0000000E+03 -9.4169609E-02 3.2041266E+00 -9.4791704E-01 2.0132122E+01
0.0926 1.0800510E+01 1.0000000E+04 -1.2707970E-01 3.1022887E+00 -1.2385350E+00 1.9492256E+01
0.0806 1.2410323E+01 1.1000000E+04 -1.7764316E-01 2.9698608E+00 -1.6574273E+00 1.8660187E+01
0.0692 1.4461029E+01 1.2000000E+04 -2.6533854E-01 2.7804081E+00 -2.3177083E+00 1.7469820E+01
0.0563 1.7746962E+01 1.3000000E+04 -4.5110229E-01 2.4544027E+00 -3.4783297E+00 1.5421468E+01
0.0353 2.8367121E+01 1.4000000E+04 -1.0730885E+00 1.6536337E+00 -5.5747414E+00 1.0390087E+01
0.0000 9.9999996E+24 1.5000000E+04 3.2813221E-02 0.0000000E+00 3.5911825E+00 0.0000000E+00
Pt C
Pt D
Слайд 68
Тон 1, M = 0.5: -10,000ft
.....
CONFIGURATION =

AEROSG2D XY-SYMMETRY = ASYMMETRIC XZ-SYMMETRY
= SYMMETRIC
POINT = 17 MACH NUMBER = 0.5000 DENSITY RATIO = 1.3273E+00 METHOD = PK
KFREQ 1./KFREQ VELOCITY DAMPING FREQUENCY COMPLEX EIGENVALUE
0.5301 1.8862758E+00 2.0000000E+03 -7.0417374E-03 3.5526409E+00 -7.8592487E-02 2.2321901E+01
0.3519 2.8420136E+00 3.0000000E+03 -1.1186195E-02 3.5368907E+00 -1.2429507E-01 2.2222940E+01
0.2622 3.8134005E+00 4.0000000E+03 -1.6010020E-02 3.5145853E+00 -1.7677295E-01 2.2082790E+01
0.2081 4.8063788E+00 5.0000000E+03 -2.1754004E-02 3.4856079E+00 -2.3821418E-01 2.1900721E+01
0.1716 5.8275118E+00 6.0000000E+03 -2.8659945E-02 3.4498055E+00 -3.1061316E-01 2.1675768E+01
0.1453 6.8844190E+00 7.0000000E+03 -3.7044190E-02 3.4068835E+00 -3.9648545E-01 2.1406080E+01
0.1252 7.9866099E+00 8.0000000E+03 -4.7379721E-02 3.3562479E+00 -4.9957010E-01 2.1087929E+01
0.1093 9.1468325E+00 9.0000000E+03 -6.0378928E-02 3.2968433E+00 -6.2536502E-01 2.0714678E+01
0.0963 1.0383610E+01 1.0000000E+04 -7.7175222E-02 3.2268453E+00 -7.8235871E-01 2.0274868E+01
0.0853 1.1726433E+01 1.1000000E+04 -9.9699713E-02 3.1430643E+00 -9.8445767E-01 1.9748455E+01
0.0756 1.3227665E+01 1.2000000E+04 -1.3152270E-01 3.0396569E+00 -1.2559582E+00 1.9098728E+01
0.0667 1.4994147E+01 1.3000000E+04 -1.7995365E-01 2.9050128E+00 -1.6423231E+00 1.8252735E+01
0.0578 1.7290926E+01 1.4000000E+04 -2.6216343E-01 2.7129159E+00 -2.2343867E+00 1.7045753E+01
0.0476 2.1013844E+01 1.5000000E+04 -4.2792672E-01 2.3917305E+00 -3.2153745E+00 1.5027687E+01
Pt D
Слайд 69
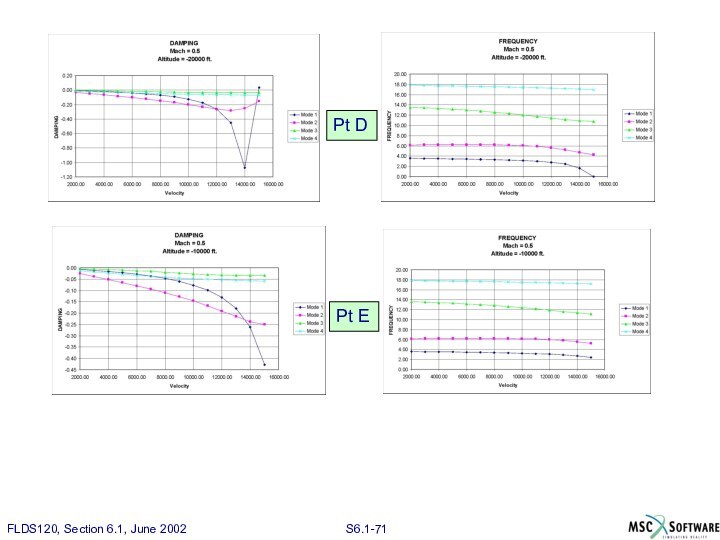
Графики V-g и V-f
На следующей странице представлены графики
V-g и V-f, на которых изображены точки пересечения A
... E.
Слайд 72
Пояснения к графикам V-g и V-f
Как видно из
графиков для точек A ... D, для первого тона
наблюдается сначала быстрый спад демпфирования, а потом резкий рост до положительных значений.
Из графиков для точек A ... D видно, что частота, при пересечении значений демпфирования нуля, падает до нуля. Это означает статическую дивергенцию.
В точке E наблюдается такая же тенденция, однако расчет ограничивается скоростью 15000ft/s, что приводит к неполному отображению характера изменения кривых.
Слайд 73
Пояснения к графикам V-g и V-f
Для других тонов,
для первых нескольких графиков V-g, наблюдается аналогичная картина, но
для построения остальных графиков картина немного изменяется из-за ограниченного числа значений скоростей.
Сопоставьте все полученные результаты с приведенными графиками.
Слайд 74
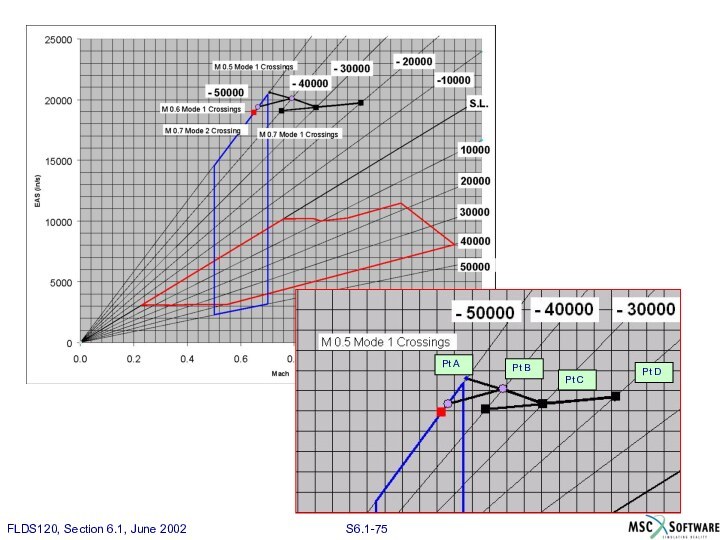
Проверка точек согласования
Точки перечесения A ... D первого
тона, изображенные на диаграмме M-EAS, размещены по высоте и
TAS.
Кривые, соединяющие точки не должны пересекать линию M = 0.5.
Таким образом, первый тон не имеет точки согласования в рассмотренной области исследования.
Слайд 76
Расчет флаттера во второй области исследования
Теперь мы исследуем
диапазон эксплуатационных режимов для чисел Маха 0.8 ... 0.97.
Посчитанные
значения kmin и kmax представлены в таблице. Мы выбрали ряд значений от .05 до 1.0 со смещением относительно центра.
Ряд скоростей выбран от 4000in/s до 21000in/s
Слайд 77
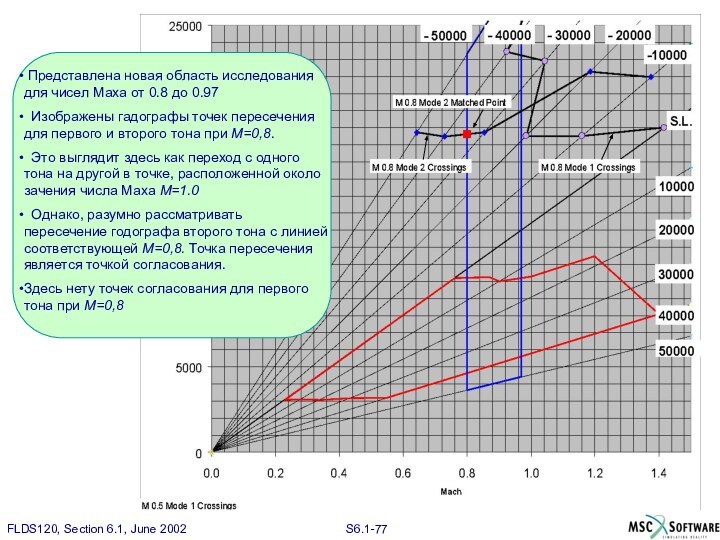
Представлена новая область исследования для чисел Маха
от 0.8 до 0.97
Изображены гадографы точек пересечения для
первого и второго тона при М=0,8.
Это выглядит здесь как переход с одного тона на другой в точке, расположенной около зачения числа Маха М=1.0
Однако, разумно рассматривать пересечение годографа второго тона с линией соответствующей М=0,8. Точка пересечения является точкой согласования.
Здесь нету точек согласования для первого тона при М=0,8
Слайд 78
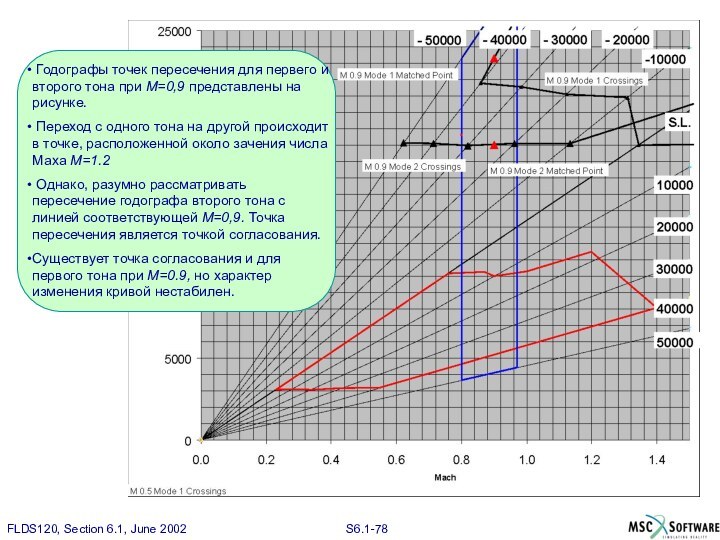
Годографы точек пересечения для первего и второго
тона при М=0,9 представлены на рисунке.
Переход с одного
тона на другой происходит в точке, расположенной около зачения числа Маха М=1.2
Однако, разумно рассматривать пересечение годографа второго тона с линией соответствующей М=0,9. Точка пересечения является точкой согласования.
Существует точка согласования и для первого тона при М=0.9, но характер изменения кривой нестабилен.
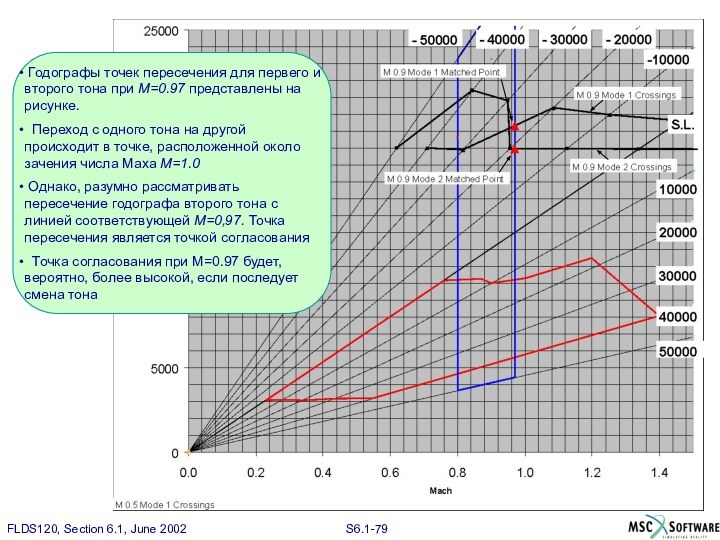
Слайд 79
Годографы точек пересечения для первего и второго
тона при М=0.97 представлены на рисунке.
Переход с одного
тона на другой происходит в точке, расположенной около зачения числа Маха М=1.0
Однако, разумно рассматривать пересечение годографа второго тона с линией соответствующей М=0,97. Точка пересечения является точкой согласования
Точка согласования при М=0.97 будет, вероятно, более высокой, если последует смена тона
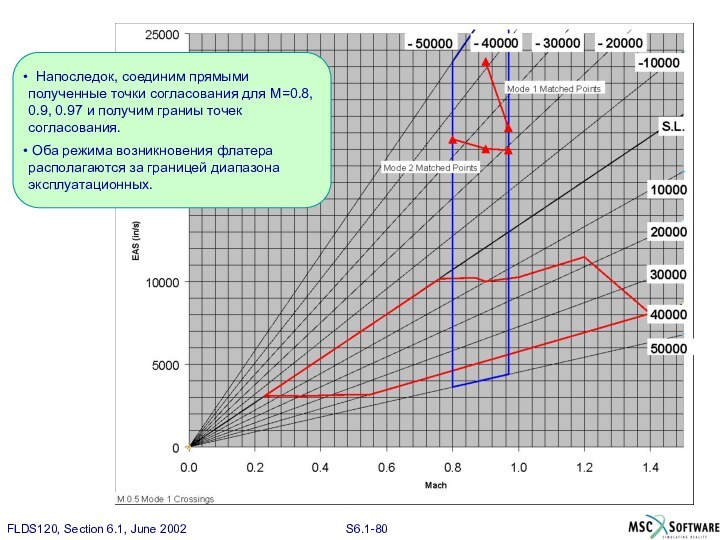
Слайд 80
Напоследок, соединим прямыми полученные точки согласования для
М=0.8, 0.9, 0.97 и получим граниы точек согласования.
Оба
режима возникновения флатера располагаются за границей диапазона эксплуатационных.
Слайд 81
Расчет флаттера в третьей области исследования
Теперь мы исследуем
диапазон эксплуатационных режимов для чисел Маха 1.03 ... 1.5.
Посчитанные
значения kmin и kmax представлены в таблице. Мы выбрали ряд значений от .02 до 1.0 со смещением относительно центра.
Ряд скоростей выбран от 6000in/s до 30000in/s
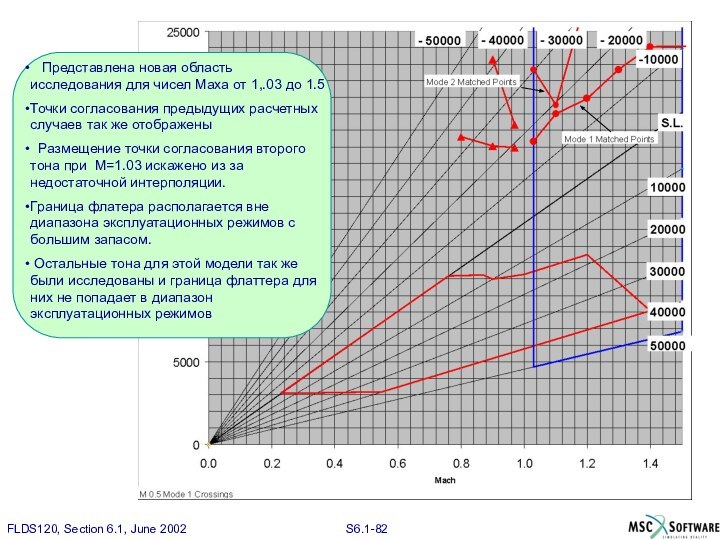
Слайд 82
Представлена новая область исследования для чисел
Маха от 1,.03 до 1.5
Точки согласования предыдущих расчетных случаев
так же отображены
Размещение точки согласования второго тона при M=1.03 искажено из за недостаточной интерполяции.
Граница флатера располагается вне диапазона эксплуатационных режимов с большим запасом.
Остальные тона для этой модели так же были исследованы и граница флаттера для них не попадает в диапазон эксплуатационных режимов
Слайд 83
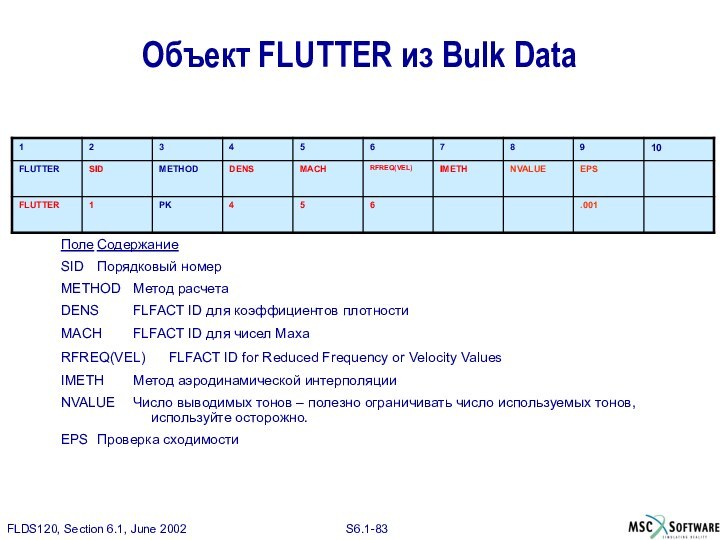
Объект FLUTTER из Bulk Data
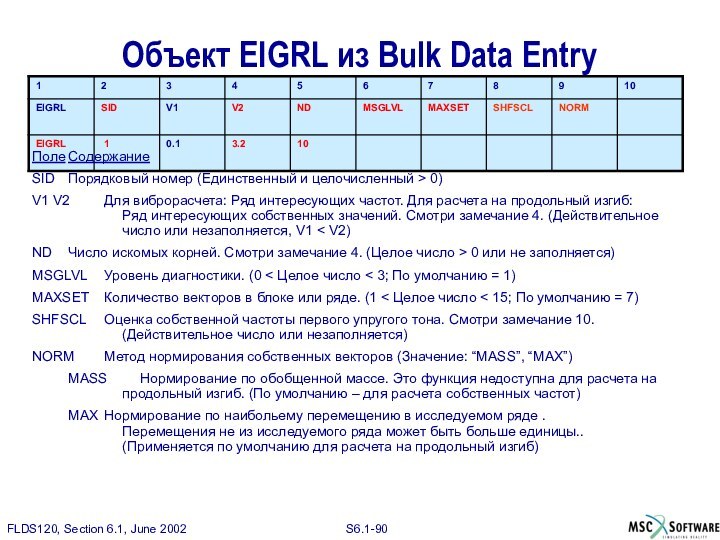
Поле Содержание
SID Порядковый номер
METHOD Метод расчета
DENS FLFACT ID
для коэффициентов плотности
MACH FLFACT ID для чисел Маха
RFREQ(VEL) FLFACT ID
for Reduced Frequency or Velocity Values
IMETH Метод аэродинамической интерполяции
NVALUE Число выводимых тонов – полезно ограничивать число используемых тонов, используйте осторожно.
EPS Проверка сходимости
Слайд 84
Объект FLUTTER из Bulk Data
SID ссылается на FMETHOD
из Case Control FMETHOD = SID
Расчетная плотность = RHOREF*плотность
из объекта FLFACT ссылающегося на DENS
RHOREF задается в объекте AERO из bulk data.
Слайд 85
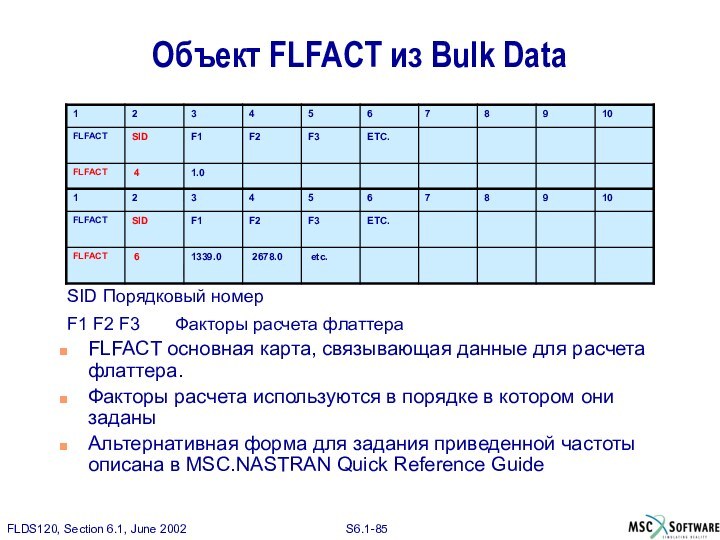
Объект FLFACT из Bulk Data
FLFACT основная карта, связывающая
данные для расчета флаттера.
Факторы расчета используются в порядке в
котором они заданы
Альтернативная форма для задания приведенной частоты описана в MSC.NASTRAN Quick Reference Guide
Поле Содержание
SID Порядковый номер
F1 F2 F3 Факторы расчета флаттера
Слайд 86
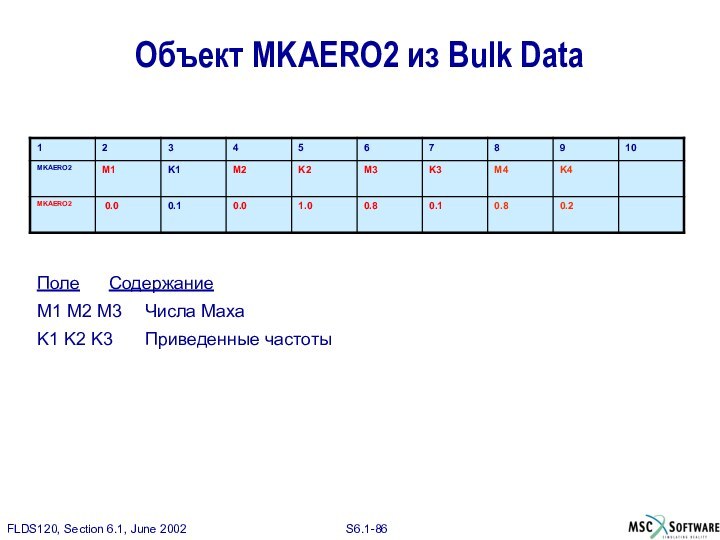
Поле Содержание
M1 M2 M3 Числа Маха
K1 K2 K3 Приведенные частоты
Объект
MKAERO2 из Bulk Data
Слайд 87
Объект MKAERO2 из Bulk Data
Часла Маха могут только
быть ≥ 0.0,
Сверхзвуковые значения чисел Маха и активируют метод
Зона51 (если включена опция Aero II)
Дозвуковые – метод дипольных решеток
Приведенная частота должна быть > 0.0
Перенос не допускается. Дополнительные данные могут быть заданы с использование дополнительных объектов.
Все значения M и K будут использоваться при вычислении аэродинамических матриц
Слайд 88
Объект MKAERO1 из Bulk Data
Поле Содержание
M1 M2 M3 Числа Маха
K1
K2 K3 Приведенная частота
Альтернативная форма ввода, не поддерживается в
FLDS
Слайд 89
Объект MKAERO1 из Bulk Data
Часла Маха могут только
быть ≥ 0.0,
Сверхзвуковые значения чисел Маха и активируют метод
Зона51 (если включена опция Aero II)
Дозвуковые – метод дипольных решеток
Приведенная частота должна быть > 0.0
Требуется один и только один перенос. Дополнительные данные могут быть заданы с использование дополнительных объектов.
Все значения M и K будут использоваться при вычислении аэродинамических матриц