lagrange1.dat
$
SOL 105
CEND
TITLE = BUCKLING ANALYSIS - RBAR
SUBTI =
LAGRANGE ELIMINATION METHOD
DISP = ALL
SPC = 10
RIGID = LGELIM
SUBCASE 1
LABEL=STATIC PRELOAD CASE
LOAD = 100
SUBCASE 2
LABEL = BUCKLING CASE
METHOD = 10
BEGIN BULK
EIGRL,10,,,10
FORCE,100,4 ,0,-100.0,1.0,0.0,0.0
CELAS2,101,100.0,3,5
CELAS2,102,120.0,3,6
GRID, 3 ,,2.0,0.0,0.0
GRID, 4 ,,4.0,0.0,0.0
RBAR, 3,3,4,123456, , ,123456
SPC1,10,1234,3
ENDDATA
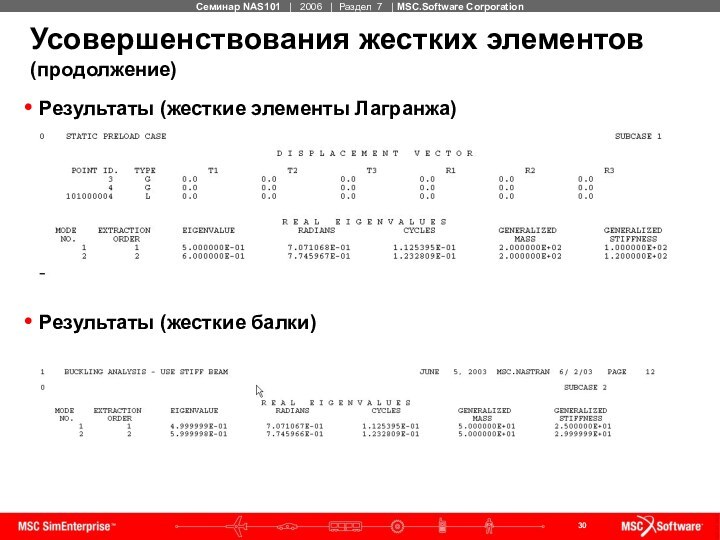
Входной файл (жесткие балки)
$
$ lagrange2.dat
$
SOL 105
CEND
TITLE = BUCKLING ANALYSIS - USE STIFF BEAM
DISP = ALL
SPC = 10
SUBCASE 1
LABEL=STATIC PRELOAD CASE
LOAD = 100
SUBCASE 2
LABEL = BUCKLING CASE
METHOD = 10
BEGIN BULK
EIGRL,10,,,10
FORCE,100,4 ,0,-100.0,1.0,0.0,0.0
CELAS2,101,100.0,3,5
CELAS2,102,120.0,3,6
CBEAM,100,100,3,4,0.,0.,1.
PBEAM,100,1,100.,100.,100.,,100.
MAT1,1,1.E7,,.32
GRID, 3 ,,2.0,0.0,0.0
GRID, 4 ,,4.0,0.0,0.0
SPC1,10,1234,3
ENDDATA



![MSC.Nastran 101 2006 - 7 Решение задачи на собственные значения [ K – λKd ] {φ} = 0 (1) Решение](/img/tmb/11/1040348/4c3647b46ff3cea1d4b363d240245363-720x.jpg)