Слайд 2
Раздел 1. Обзор основ динамического анализа
ПРОЦЕСС ДИНАМИЧЕСКОГО АНАЛИЗА……………………………………..…………
1 - 4
СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ…………………….……………………
1 - 5
СИСТЕМА ЕДИНИЦ…...……………………………………………………….……………. 1 - 6
НЕЗАТУХАЮЩИЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (СС)..………………………………………………………………... 1 - 9
ЗАТУХАЮЩИЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ……………………………………………………..………………..……………….. 1- 11
СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - ПОДКРИТИЧЕСКОЕ ДЕМПФИРОВАНИЕ………………………………………………………………………….…. 1 - 13
СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ – НЕЗАТУХАЮЩИЕ СИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ…………………………………………………..…….. 1 - 14
ДИНАМИЧЕСКИЙ ФАКТОР………………………………………………..…………………. 1 - 16
СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ – ЗАТУХАЮЩИЕ СИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ…………..………………….………..……………..…. 1 - 17
ДИНАМИЧЕСКИЙ ФАКТОР.…………………………………...……………………………… 1 -19
Слайд 3
Обзор основ динамического анализа (продолж.)
СИСТЕМА С МНОГИМИ СТЕПЕНЯМИ
СВОБОДЫ.……………….……………………. 1 - 20
ТИПЫ КОЛЕБАНИЙ…………………………..………………………………………………. 1 - 21
ВИДЫ
ДИНАМИЧЕСКОГО ВОЗДЕЙСТВИЯ ……………………………...……………… 1 - 22
ВОПРОСЫ МОДЕЛИРОВАНИЯ ДИНАМИКИ МЕТОДОМ КЭ……….…………………. 1 - 23
ДОКУМЕНТАЦИЯ ПО СИСТЕМЕ MSC.Nastran ...…...………………..…………………...1 - 24
ЛИТЕРАТУРА ПО ДИНАМИЧЕСКОМУ АНАЛИЗУ…………………...…………………….1 - 26
Слайд 4
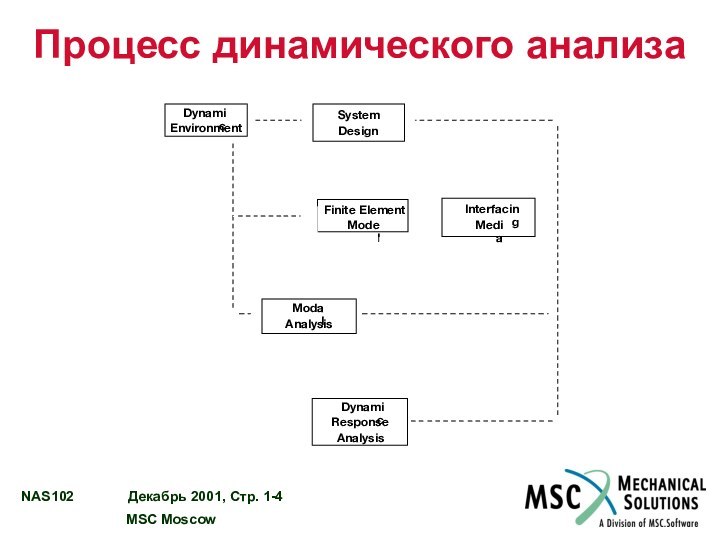
Процесс динамического анализа
Слайд 5
Система с одной степенью свободы
Уравнение движения:
mu(t) + bu(t)
+ ku(t) = p(t) + n(u,u)
m = масса
b =
демпфирование
k = жесткость
n = нелинейная восстанавливающая сила
p = внешняя сила
u = перемещение
u = скорость
u = ускорение
u, u, u и p зависят от времени.
m, b и k - константы.
n – нелинейная функция u, u.
.
..
..
..
.
.
.
.
.
.
Слайд 6
Система единиц
Основные единицы
Основные и производные единицы
Длина L (дюйм, метр)
Масса
M (слаг,килограмм)
Время T (секунда)
Длина L (метр, миллиметр)
Сила F (Ньютон)
Время T (секунда)
m M
b MT -1
k MT -2
p MLT -2
u L
u LT
-1
u LT -2
m FT2/L = F/(LT –2)
b FT/L = F/(T/L)
k F/L
p F
u L
u LT -1
u LT -2
.
.
..
..
Слайд 7
Система единиц
Техническая система единиц.
*L размерность длины
M размерность
массы
T размерность времени
- безразмерная величина
Слайд 8
Система единиц
Используйте согласованную систему единиц!
Ошибки в выборе системы
единиц – причина №1 при подготовке модели для динамического
анализа!
Наиболее частые ошибки – при выборе единиц для параметров массы и демпфирования.
В MSC.Nastran нет “встроенной” системы единиц. Пользователь сам должен проверять согласованность единиц измерения величин.
Согласованные единицы: Н, тм, мм, с или Н, кг, м, с
Слайд 9
Незатухающие свободные колебания системы с одной СС
Уравнение колебаний
Общее
решение
Начальные условия
Результат
u(0) и u(0) - известны.
.
Слайд 10
Незатухающие свободные колебания системы с одной СС
Слайд 11
Затухающие свободные колебания системы с одной СС
Уравнение колебаний
Критическое
демпфирование
Коэффициент апериодичности
Влияние величины демпфирования на тип решения.
Подкритическое демпфирование
Частота колебаний
системы с демпфированием
Слайд 12
Затухающие свободные колебания системы с одной СС
Критическое демпфирование
b
= bc
Колебания отсутствуют.
u(t) = (A + Bt) e-bt/2m
Надкритическое демпфирование
b
> bc
Колебания отсутствуют. Система постепенно возвращается в положение равновесия.
Обычно исследуются колебания с подкритическим демпфированием.
Для конструкций характерно вязкое демпфирование в диапазоне 0 – 0,1.
Слайд 13
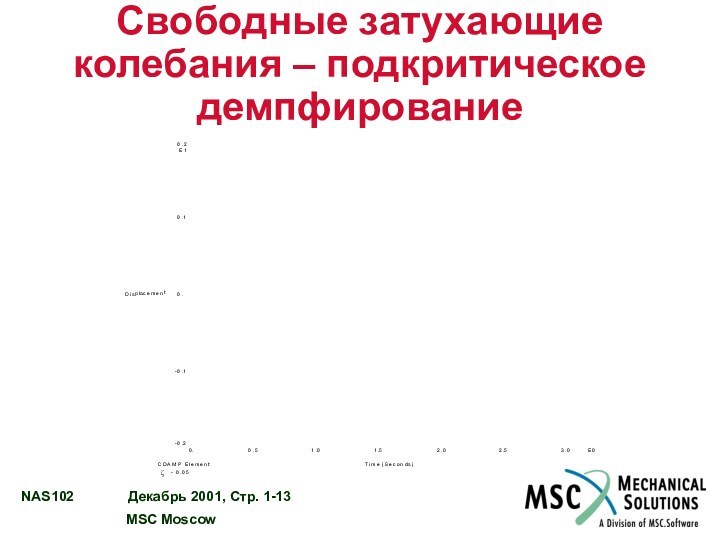
Свободные затухающие колебания – подкритическое демпфирование
Слайд 14
Система с одной СС – незатухающие синусоидальные колебания
Уравнение
колебаний
где ω = частота внешней силы
Решение
где
Слайд 15
Система с одной СС – незатухающие синусоидальные колебания
Установившиеся
колебания
P/k – статическая деформация (перемещение).
-
динамический фактор.
Слайд 17
Система с одной СС – затухающие синусоидальные колебания
Уравнение
колебаний
Переходный процесс быстро затухает и не представляет интереса.
Установившиеся
колебания
θ – сдвиг (запаздывание) фазы
Слайд 18
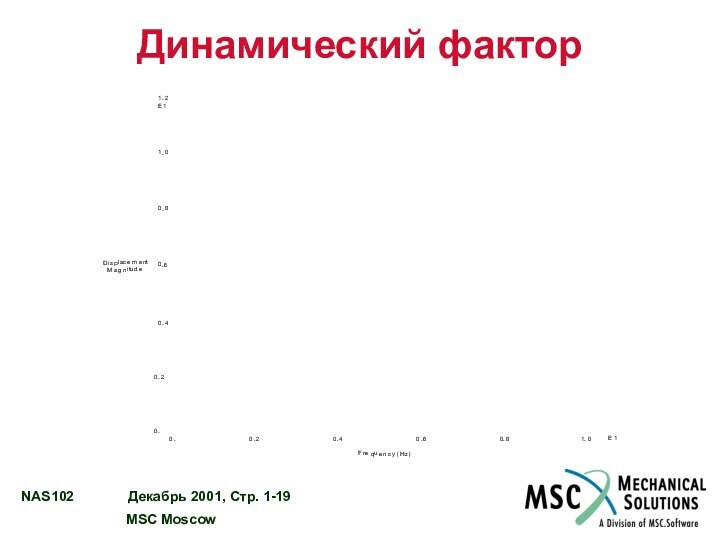
Система с одной СС – затухающие синусоидальные колебания
Для
Динамический
фактор 1 (статическое решение)
Фазовый угол
360° (отклик синфазен возмущению)
Для
Динамический фактор 0 (отклик ноль)
Фазовый угол 180° (отклик противофазен возмущению)
Для
Динамический фактор
Фазовый угол ≈ 270°
Слайд 20
Система с многими степенями свободы
Уравнение колебаний преобразуется к
виду
где
{u} = вектор перемещений
{M}= матрица масс
{B}= матрица демпфирования
{K}= матрица
жесткости
{P}= вектор внешнего воздействия
{N}= вектор нелинейных сил
Слайд 23
Вопросы моделирования динамики методом КЭ
Частотный диапазон
Узлы/закрепления/элементы
Линейное и нелинейное
решение
“Полная” модель и модель с суперэлементами
Взаимодействие с внешней средой
Сравнительный/совместный
анализ расчетных и экспериментальных результатов
Демпфирование
Слайд 24
Документация по системе MSC.Nastran
Документация
MSC.Nastran Quick Reference Guide
MSC.Nastran Reference
Manual
Руководства пользователя
Getting Started with MSC.Nastran
MSC.Nastran Linear Static Analysis
MSC.Nastran Basic
Dynamic Analysis
MSC.Nastran Advanced Dynamic Analysis
MSC.Nastran Design Sensitivity and Optimization
MSC.Nastran DMAP Module Dictionary
MSC.Nastran Numerical Methods
MSC.Nastran Aeroelastic Analysis
MSC.Nastran Thermal Analysis
Слайд 25
Документация по системе MSC.Nastran
Другая документация
MSC.Nastran Common Questions and
Answers
MSC.Nastran Bibliography
Документация в электронной форме (для рабочих станций и
персональных компьютеров)
Слайд 26
Литература по динамическому анализу
W. C. Hurty and M.
F. Rubinstein, Dynamics of Structures, Prentice-Hall, 1964.
R. W. Clough
and J. Penzien, Dynamics of Structures, McGraw-Hill, 1975.
S. Timoshenko, D. H. Young, and W. Weaver, Jr., Vibration Problems in Engineering, 4th Ed., John Wiley & Sons, 1974.
K. J. Bathe and E. L. Wilson, Numerical Methods in Finite Element Analysis, Prentice-Hall, 1976.
J. S. Przemieniecki, Theory of Matrix Structural Analysis, McGraw-Hill, 1968.
C. M. Harris and C. E. Crede, Shock and Vibration Handbook, 2nd Ed., McGraw-Hill, 1976.
L. Meirovitch, Analytical Methods in Vibrations, MacMillan, 1967.
L. Meirovitch, Elements of Vibration Analysis, McGraw-Hill, 1975.
M. Paz, Structural Dynamics Theory and Computation, Prentice-Hall, 1981.
Слайд 27
Литература по динамическому анализу
W. T. Thomson, Theory of
Vibrations with Applications, Prentice-Hall, 1981.
R. R. Craig, Structural Dynamics:
An Introduction to Computer Methods, John Wiley & Sons, 1981.
S. H. Crandall and W. D. Mark, Random Vibration in Mechanical Systems, Academic Press, 1963.
J. S. Bendat and A. G. Piersol, Random Data Analysis and Measurement Techniques, 2nd Ed., John Wiley & Sons, 1986.