Слайд 2
Раздел 5.
Бездеформационные моды колебаний
БЕЗДЕФОРМАЦИОННЫЕ МОДЫ И ВЕКТОРЫ.
АСПЕКТЫ ТЕОРИИ……………… 5 - 3
ВЫЧИСЛЕНИЕ БЕЗДЕФОРМАЦИОННЫХ МОД.……………………………………….
5 - 5
ВЫБОР СТЕПЕНЕЙ СВОБОДЫ ДЛЯ ОПЕРАТОРА SUPORT… ...………………….. 5 - 8
ПРОВЕРКА СТЕПЕНЕЙ СВОБОДЫ, УКАЗАННЫХ В ОПЕРАТОРЕ SUPORT…..… 5 - 9
БЕЗДЕФОРМАЦИОННЫЕ МОДЫ И ВЕКТОРЫ ………………………..…………….. 5 - 11
Слайд 3
Бездеформационные моды и векторы. Аспекты теории
Незакрепленная конструкция может
перемещаться без возникновения в ней внутренних сил и напряжений.
Например:
В случаях (a) и (b) конструкция может перемещаться как жесткое тело.
Слайд 4
Бездеформационные моды и векторы. Аспекты теории
Присутствие жестких тел
и/или механизмов обнаруживается по наличию нулевых собственных частот.
В предположении
положительной определенности матрицы масс [M], нулевые собственные значения являются результатов положительной полу-определенности матрицы жесткости, т.е.
Оператор SUPORT не закрепляет конструкцию. С помощью его определяются компоненты набора R-set. При модальном анализе R-set определяет системы координат, в которых вычисляются бездеформационные моды.
Слайд 5
Вычисление бездеформационных мод
Если определен R-set, MSC.Nastran вычисляет бездеформационные
моды следующим методом:
Шаг 1: разделение A-set
ul
ua =
ur
Шаг 2: решение для ul через ur .
Замечание: нагрузка Pr в действительности не прикладывается!
Слайд 6
Вычисление бездеформационных мод
ul
= Dm ur
где
Это используется для формирования совокупности бездеформационных мод.
Слайд 7
Вычисление бездеформационных мод
Шаг 3: Преобразования матриц
где [Mr] –
в общем случае недиагональная матрица
Методом Грама-Шмидта (Gram-Schmidt) (в модуле
READ), матрица [Mr] преобразуется к ортогональному виду с использованием вектора [φro]
Шаг 4: Вычисляются бездеформационные моды
со следующими свойствами:
Слайд 8
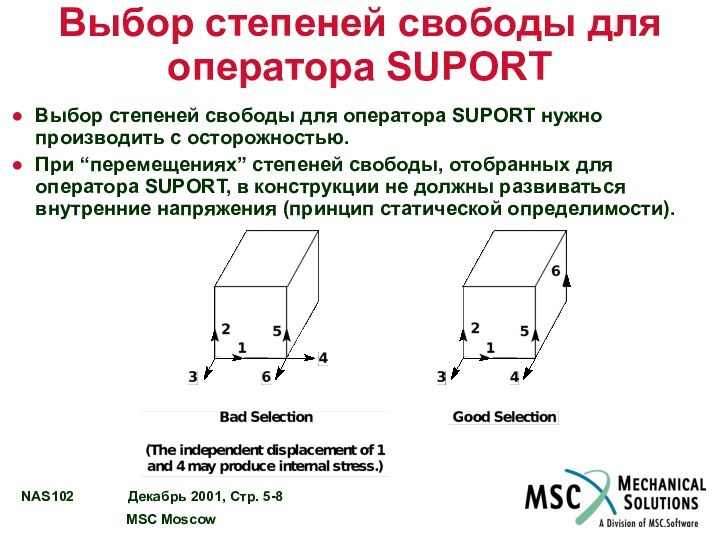
Выбор степеней свободы для оператора SUPORT
Выбор степеней свободы
для оператора SUPORT нужно производить с осторожностью.
При “перемещениях” степеней
свободы, отобранных для оператора SUPORT, в конструкции не должны развиваться внутренние напряжения (принцип статической определимости).
Слайд 9
Проверка степеней свободы, указанных в операторе SUPORT
MSC.Nastran вычисляет
энергию деформаций (работу) для каждой бездеформационной моды.
Для бездеформационной моды
энергия ≈ 0.
Заметим, что вектор [X] также является результатом преобразования матрицы жесткости [Kaa] в R-set координаты, который, по определению бездеформационных мод (нулевая собственная частота), должен быть нулевым.
MSC.Nastran также вычисляет коэффициент погрешности бездеформационной моды
где - Эйлерова норма матрицы
Замечание: для всех СС, указанных в операторе SUPORT, на основе [X] и [Krr] вычисляется только одно значение ε.
Слайд 10
Проверка степеней свободы, указанных в операторе SUPORT
Если не
принимать во внимание ошибки округления, коэффициент погрешности бездеформационной моды
и энергия деформаций должны быть равны нулю (при правильном выборе СС для оператора SUPORT). Эти величины м.б. не нулевыми по следующим причинам:
Накопление ошибок округления
“Переопределенность” ur-set (высокая энергия деформации).
“Недоопределенность” u- set – сингулярность матрицы жесткости (большое значение коэффициента погрешности).
Несовместимость межузловых связей MPC (высокая энергия деформации и большое значение коэффициента погрешности).
Излишнее количество граничных условий (высокая энергия деформации и большое значение коэффициента погрешности).
Матрица Krr нулевая (коэффициент погрешности равен 1, а энергия деформаций – низкая). Это, однако, приемлемо и может иметь место при использовании обобщенного динамического редуцирования.
Слайд 11
Бездеформационные моды и векторы
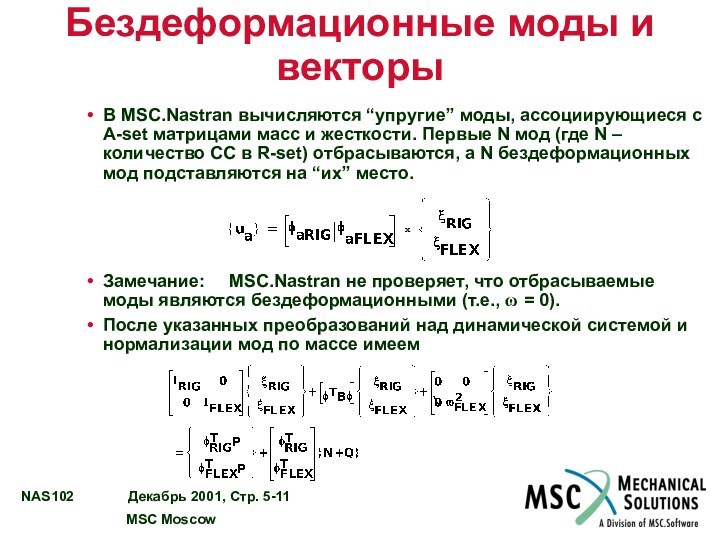
В MSC.Nastran вычисляются “упругие” моды,
ассоциирующиеся с A-set матрицами масс и жесткости. Первые N
мод (где N – количество СС в R-set) отбрасываются, а N бездеформационных мод подставляются на “их” место.
Замечание: MSC.Nastran не проверяет, что отбрасываемые моды являются бездеформационными (т.е., ω = 0).
После указанных преобразований над динамической системой и нормализации мод по массе имеем
Слайд 12
Бездеформационные моды и векторы
В результате преобразований имеем:
Усилия закреплений
отсутствуют, т.е.
Если элементы демпфирования не сопрягаются с неподвижным основанием,
то
Таким образом,
Слайд 13
Бездеформационные моды и векторы
Если демпфирование “пропорциональное”, тогда
Уравнения динамики
при модальном анализе полностью несвязанные.






![MSC.Nastran 102 2001 - 05 Вычисление бездеформационных модШаг 3: Преобразования матрицгде [Mr] – в общем случае недиагональная](/img/tmb/11/1042083/40714f4af7a1ebf6c535c71490f05e78-720x.jpg)