- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нечеткая логика
Содержание
- 2. Плохая формализуемость ОУ* Наиболее
- 3. Немного теорииНечеткая логика основана на использовании оборотов
- 4. Впервые термин нечеткая логика (fuzzy logic) был
- 5. Термин "нечеткая логика"В узком смысле, нечеткая логика
- 6. Примеры применения нечеткой логики Автоматическое управление воротами
- 7. Оптимизированное планирование автобусных расписаний (Toshiba). Системы архивации
- 8. Распознавание рукописных символов в карманных компьютерах (записных
- 9. Управление метрополитенами для повышения удобства вождения, точности
- 10. Определение. Пусть X – универсальное множество. Тогда
- 11. Определение. Нечеткое множество называется пустым, если μ
- 12. В феврале 1991 года была сконструирована первая
- 13. Бурный рост рынка нечетких системЕсли рассматривать финансово-экономический
- 14. Пример Прогноз погоды на завтра температура
- 15. Недостатки нечетких системотсутствие стандартной методики конструирования нечетких
- 16. Области эффективного применения современных технологий управления Как
- 17. БАЗОВЫЕ ПОНЯТИЯ НЕЧЕТКОЙ ЛОГИКИОпределение µА(x) – характеристическая
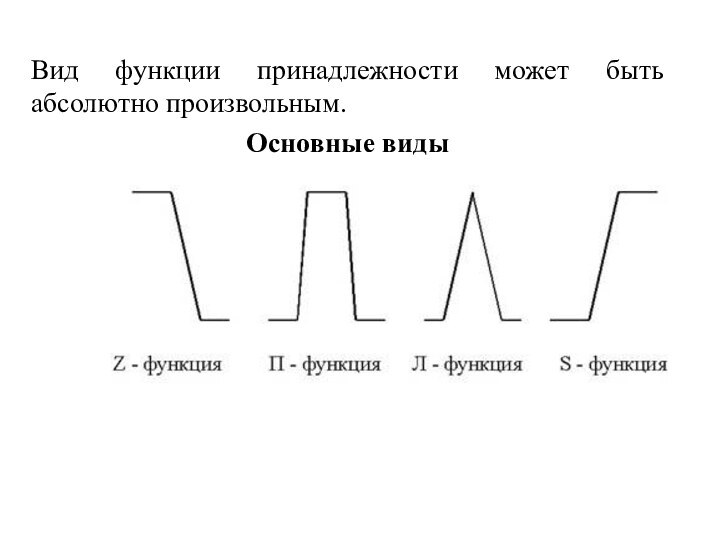
- 18. Вид функции принадлежности может быть абсолютно произвольным.Основные виды
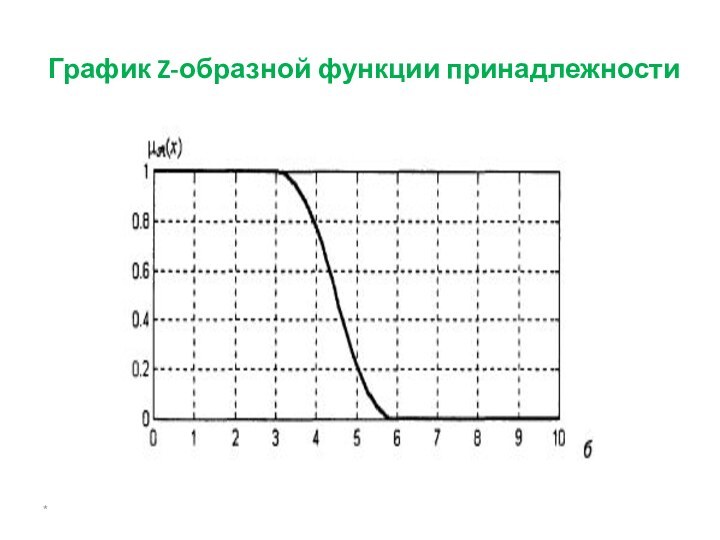
- 19. Z-образная функция принадлежности*
- 20. График Z-образной функции принадлежности*
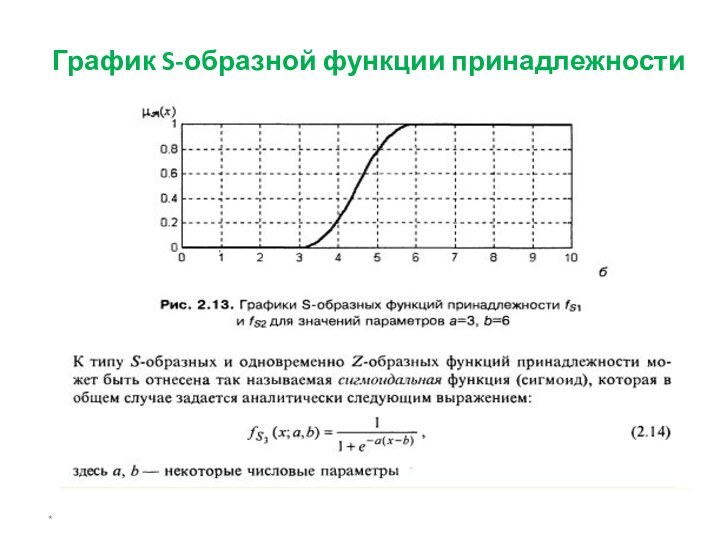
- 21. S-образная функция принадлежности*
- 22. График S-образной функции принадлежности*
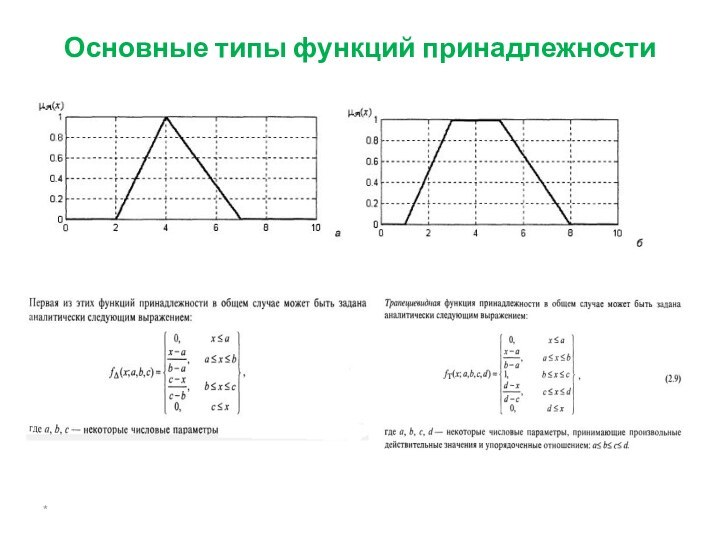
- 23. Основные типы функций принадлежности*
- 24. Гауссова функция принадлежности *Функция принадлежности гауссова типа
- 25. Примеры лингвистических переменных*Рис.3. Описание лингвистической переменной 'Цена
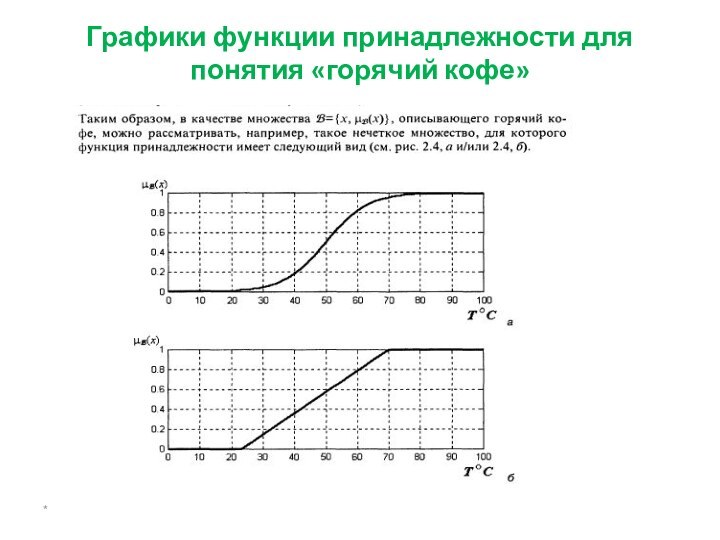
- 26. Графики функции принадлежности для понятия «горячий кофе»*
- 27. Основные характеристики нечетких множеств 1. Величина µА(х)
- 29. Операции с нечеткими множествами *К нечетким множествам
- 30. Операции над нечеткими множествами*
- 31. Пример 1. Нечеткое множество для термина
- 32. Функция принадлежности нечеткого множества “Оптимальный возраст работающих”
- 33. Принципы работы систем с нечеткой логикойФаззификация:
- 34. Определение. Фаззификация - сопоставление множества значений х
- 35. Понятие лингвистической переменной Определение. Лингвистическая переменная -
- 36. Определение числа термов Исходите из стоящей перед
- 37. Лингвистическая переменнаяОпределяете необходимое число термов и каждому
- 38. Пример1. Лингвистическая переменная ВОЗРАСТ для нее термы
- 39. Правило продукцийСостоит из посылок и заключения. Возможно
- 40. ПримерМожно задать степень принадлежности к терму ОЧЕНЬ БЛИЗКО равную 0.7, а к терму БЛИЗКО – 0.3.
- 41. Алгоритм по формализации задачи в терминах нечеткой
- 42. Алгоритмы нечеткого вывода*Среди других алгоритмов нечеткого вывода,
- 43. Алгоритм Сугэно*Исходный набор правил представляется в виде
- 44. Алгоритм Сугэно*Алгоритм Сугэно (0-го порядка). Исходный набор
- 45. *Метод выбора тестов при помощи алгоритма Сугено
- 46. *Результаты выбора тестов по алгоритму Сугено
- 47. Операции нечеткого вывода*Фаззификация (переход к нечеткости)Точные значения
- 48. Структура системы нечеткого управления *
- 49. Моделирование работы светофора с нечеткой логикой
- 50. В нечетком светофоре время цикла остается постоянным,
- 51. Светофор использует разности показаний четырех пар датчиков:
- 52. Показатель эффективности - число машин, не проехавших
- 53. Для переменной время зеленого света предлагается три терма: малое (10-25сек.); среднее(20-40сек.); большое(35-50сек.).
- 54. Функция принадлежности первой входной переменной
- 55. Термы для двух оставшихся переменных :очень малое
- 56. В качестве выходного параметра – время зеленого светофора.Термы: уменьшить (-20-0сек.); не изменять (-15-15сек.); увеличить (0-20сек.).
- 57. Таблица правил на основе условных высказываний формирует
- 58. Результаты моделирования работы светофора с нечеткой логикой
- 59. Результат работы
- 60. Скачать презентацию
- 61. Похожие презентации
Плохая формализуемость ОУ* Наиболее продвинутые на сегодня методы построения автоматических систем управления основаны на использовании строгих математических моделей объектов. Однако, для подавляющего большинства как искусственных, так и естественных объектов управления (ОУ), которыми необходимо












































Слайд 3
Немного теории
Нечеткая логика основана на использовании оборотов естественного
языка - «далеко», «близко», «холодно», «горячо».
Диапазон ее применения
- от бытовых приборов до управления сложными промышленными процессами. Многие задачи управления просто не могут быть решены классическими методами из-за очень большой сложности математических моделей.
Слайд 4 Впервые термин нечеткая логика (fuzzy logic) был введен
амерканским профессором Лотфи Заде в 1965 году в работе
“Нечеткие множества” в журнале “Информатика и управление”.Побудительным мотивом представления Л. Заде идеи и теории нечетких множеств стала необходимость описания таких явлений и понятий, которые имеют многозначный и неточный характер. Известные до этого математические методы, использовавшие классическую теорию множеств и двузначную логику, не позволяли решать проблемы этого типа.
Родился в БакуРодился в Баку, Азербайджан как Лотфи Алескерзаде (или Аскер Заде) от русской матери и отца азербайджанца иранского происхождения; с 1932) от русской матери и отца азербайджанца иранского происхождения; с 1932 года жил в Иране) от русской матери и отца азербайджанца иранского происхождения; с 1932 года жил в Иране, учился Тегеранском университете; с 1944 в Соединенных Штатах; работает в Калифорнийском университете (Беркли).
Слайд 5
Термин "нечеткая логика"
В узком смысле,
нечеткая логика —
это логическое исчисление, являющееся расширением многозначной логики.
В широком
смысленечеткая логика равнозначна теории нечетких множеств.
Нечеткая логика в узком смысле является разделом нечеткой логики в широком смысле.
Слайд 6
Примеры применения нечеткой логики
Автоматическое управление воротами плотины
на гидроэлектростанциях.
Упрощенное управление роботами.
Наведение телекамер при трансляции спортивных
событий.Эффективное и стабильное управление автомобильными двигателями.
Управление экономичной скоростью автомобилей (Nissan, Subaru).
Слайд 7
Оптимизированное планирование автобусных расписаний (Toshiba).
Системы архивации документов
(Mitsubishi Elec.).
Системы прогнозирования землетрясений (Japan).
Диагностика рака (Kawasaki
Medical School).Финансисты, задачи которых требуют ежедневного принятия правильных решений в сложных условиях непредвиденного рынка (FujiBankпо).
Промышленные гиганты США. Motorola, General Electric, OtisElevator, PacificGas&Electric, Ford и другие.
Слайд 8 Распознавание рукописных символов в карманных компьютерах (записных книжках)
(Sony).
Однокнопочное управление стиральными машинами (Matsushita, Hitatchi).
Распознавание
рукописных текстов, объектов, голоса (CSK, Hitachi, Hosai Univ., Ricoh). Слайд 9 Управление метрополитенами для повышения удобства вождения, точности остановки
и экономии энергии (Hitachi).
Оптимизация потребления бензина в автомобилях
(NOK, Nippon Denki Tools). Повышение чувствительности и эффективности управления лифтами (Fujitec, Hitachi, Toshiba).
Слайд 10 Определение. Пусть X – универсальное множество. Тогда подмножество
A в X есть совокупность пар A={x,μA(x)}, где, μA(x)
– функция, определяющая степень принадлежности элемента x к A; область ее значений лежит в интервале (μA(x)/X)∈[0,1].Для обычного четкого множества A можно положить
Слайд 11 Определение. Нечеткое множество называется пустым, если μ A(x)
= 0 для всех x∈X.
Пример
Пусть
X – множество студентов, А - множество пожилых людей. Нечеткое множество А – пустое, μ A(x) = 0 для всех x∈X, так как пожилых студентов, вообще говоря, не бывает.
Слайд 12 В феврале 1991 года была сконструирована первая
стиральная машина, в системе управления которой сочетались нечеткая логика.
Автоматически определяя нечеткие входные факторы:
объем и качество белья,
уровень загрязненности,
тип порошка и т.д.,
Стиральная машина выбирала оптимальный режим стирки из 3800 возможных.
Слайд 13
Бурный рост рынка нечетких систем
Если рассматривать финансово-экономический сектор,
то по мнению А.О. Недосекина, сотрудника компании Siemens Business
Services Russia, доктора экономических наук: «Поток публикаций по применению нечетких множеств в экономическом и финансовом анализе растет лавинообразно. Международная ассоциация International Association for Fuzzy-Set Management & Economy (SIGEF) регулярно апробирует новые результаты в области нечетко-множественных экономических исследований. Исследователями написано несколько сотен монографий по этой проблематике. В России этот процесс тоже набирает обороты.
Слайд 14
Пример
Прогноз погоды на завтра
температура воздуха
+10 градусов С, возможен дождь.
Это и есть проявление
нечеткой логики: погода завтра может быть в данном случае как просто пасмурной, так и дождливой: события здесь предсказываются с некоторой долей уверенности (рангом).
Слайд 15
Недостатки нечетких систем
отсутствие стандартной методики конструирования нечетких систем;
невозможность математического анализа нечетких систем существующими методами;
применение нечеткого
подхода по сравнению с вероятностным не приводит к повышению точности вычислений.
Слайд 16
Области эффективного применения современных технологий управления
Как видно,
классические методы управления хорошо работают при полностью детерминированном объекте
управления и детерминированной среде, а для систем с неполной информацией и высокой сложностью объекта управления оптимальными являются нечеткие методы управления.
Слайд 17
БАЗОВЫЕ ПОНЯТИЯ НЕЧЕТКОЙ ЛОГИКИ
Определение µА(x) – характеристическая функция
принадлежности (функция принадлежности) - функция указывает степень (уровень) принадлежности
элемента х подмножеству А.Замечание Обычное множество - частный случай нечеткого множества.
Функцию принадлежности, как и всякую функцию, можно задавать таблично или аналитически.
Слайд 24
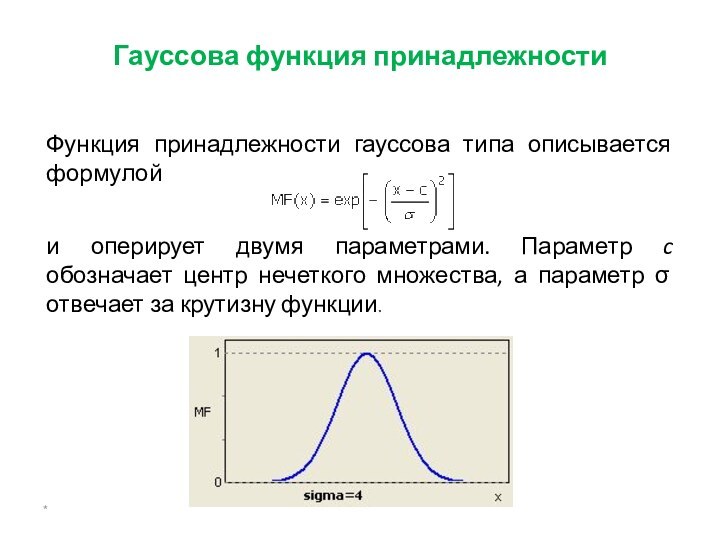
Гауссова функция принадлежности
*
Функция принадлежности гауссова типа описывается
формулой
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого
множества, а параметр σ отвечает за крутизну функции.
Слайд 25
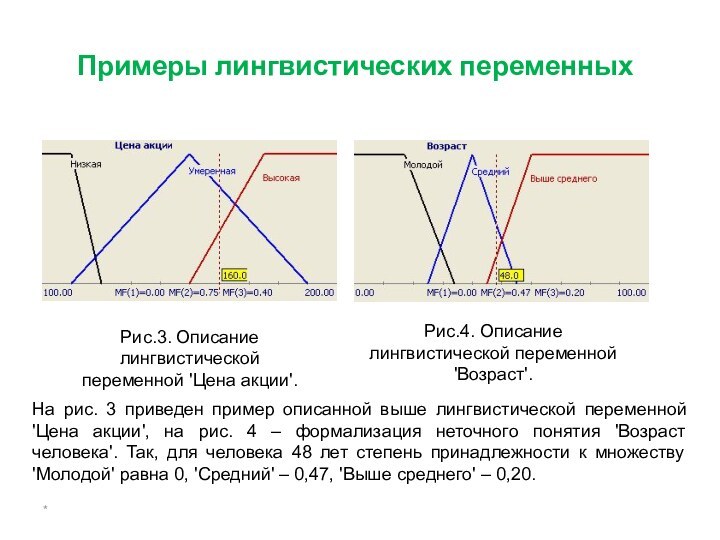
Примеры лингвистических переменных
*
Рис.3. Описание лингвистической переменной 'Цена акции'.
Рис.4. Описание лингвистической переменной 'Возраст'.
На рис. 3 приведен
пример описанной выше лингвистической переменной 'Цена акции', на рис. 4 – формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности к множеству 'Молодой' равна 0, 'Средний' – 0,47, 'Выше среднего' – 0,20.
Слайд 27
Основные характеристики нечетких множеств
1. Величина µА(х) называется высотой
нечеткого множеcтва А.
Нечеткое множество А нормально, если его
высота равна 1 , в противном случае нечеткое множество называется субнормальным.Нечеткое множество унимодально , если функция принадлежности =1 только для одного элемента.
Элементы х Є E , для которых µА(х)= 0,5, называются точками перехода множества.
Слайд 29
Операции с нечеткими множествами
*
К нечетким множествам можно применять
следующие операции:
1.объединение
2.пересечение 3.дополнение 4.концентрация 5.размывание (или размытие)
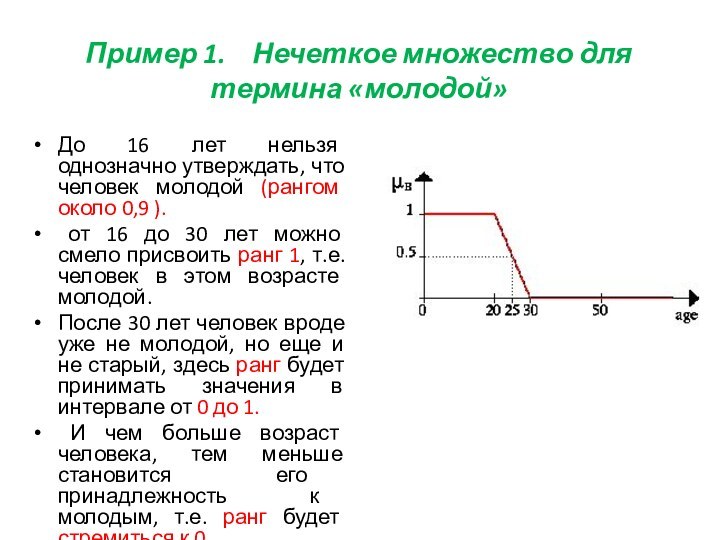
Слайд 31 Пример 1. Нечеткое множество для термина «молодой»
До 16 лет нельзя однозначно утверждать, что человек молодой
(рангом около 0,9 ). от 16 до 30 лет можно смело присвоить ранг 1, т.е. человек в этом возрасте молодой.
После 30 лет человек вроде уже не молодой, но еще и не старый, здесь ранг будет принимать значения в интервале от 0 до 1.
И чем больше возраст человека, тем меньше становится его принадлежность к молодым, т.е. ранг будет стремиться к 0.
Слайд 32
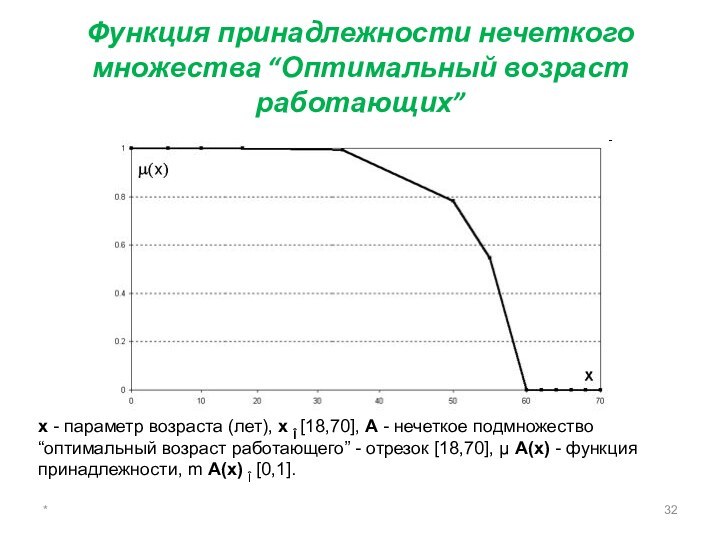
Функция принадлежности нечеткого множества “Оптимальный возраст работающих”
*
х
- параметр возраста (лет), х Î [18,70], А -
нечеткое подмножество “оптимальный возраст работающего” - отрезок [18,70], μ А(х) - функция принадлежности, m А(х) Î [0,1].
Слайд 33
Принципы работы систем с нечеткой логикой
Фаззификация:
(измерительные приборы фаззифицируются (переводятся в нечеткий формат),
Разработка нечетких правил Дефаззификация виде привычных сигналов подаются на исполнительные устройства.
Слайд 34 Определение. Фаззификация - сопоставление множества значений х ее
функции принадлежности М(х), т.е. перевод значений х в нечеткий
формат Дефаззификация - процесс, обратный фаззификации.Значения функции принадлежности μ(x) могут быть взяты только из априорных знаний, интуиции (опыта), опроса экспертов.
Слайд 35
Понятие лингвистической переменной
Определение. Лингвистическая переменная - переменная, значениями
которой являются не числа, а слова естественного языка, называемые
термами.Для большинства приложений достаточно 3-7 термов на каждую переменную. (минимальное, максимальное, среднее).
Максимальное количество термов не ограничено и зависит целиком от приложения.
Слайд 36
Определение числа термов
Исходите из стоящей перед вами
задачи и необходимой точности описания, помните, что для большинства
приложений вполне достаточно трех термов в переменной;нечеткие правила функционирования системы должны быть понятны.
Слайд 37
Лингвистическая переменная
Определяете необходимое число термов и каждому из
них ставите в соответствие некоторое значение описываемой физической величины.
Для
этого значения степень принадлежности физической величины к терму будет равна единице, а для всех остальных значений - в зависимости от выбранной функции принадлежности.
Слайд 38
Пример
1. Лингвистическая переменная ВОЗРАСТ для нее термы ЮНОШЕСКИЙ,
СРЕДНИЙ и ПРЕКЛОННЫЙ.
2. Лингвистической переменной ДИСТАНЦИЯ принадлежат термы
ДАЛЕКО, БЛИЗКО.Нечеткие системы основаны на правилах продукционного типа, в качестве посылки и заключения в правиле используются лингвистические переменные.
Слайд 39
Правило продукций
Состоит из посылок и заключения.
Возможно наличие
нескольких посылок в правиле,
они объединяются посредством логических связок
И, ИЛИ. Продукционное правило записывается в виде:
«ЕСЛИ (посылка) (связка) (посылка)… (посылка) ТО (заключение)».
Слайд 40
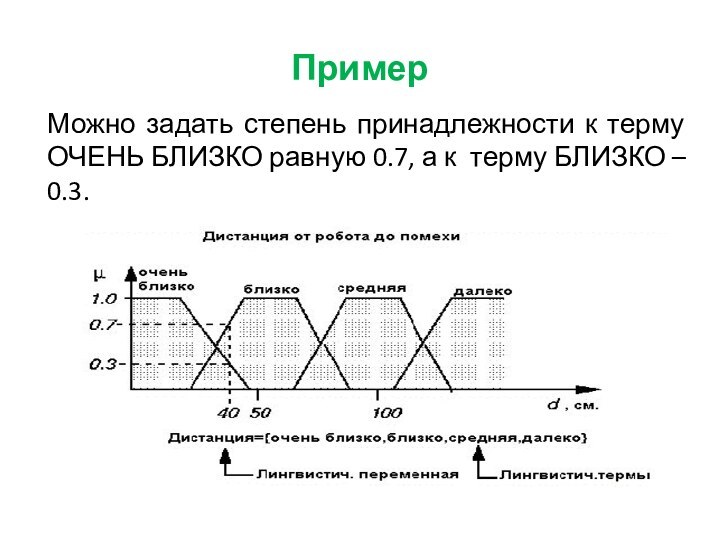
Пример
Можно задать степень принадлежности к терму ОЧЕНЬ БЛИЗКО
равную 0.7, а к терму БЛИЗКО – 0.3.
Слайд 41
Алгоритм по формализации задачи в терминах нечеткой логики
Шаг
1. Для каждого терма взятой лингвистической переменной найти числовое
значение или диапазон значений, наилучшим образом характеризующих данный терм.Шаг 2. После определения значений с единичной принадлежностью необходимо определить значение параметра с принадлежностью «0» к данному терму.
Шаг 3. Для определения промежуточных значений выбираются П- или Л-функции из числа стандартных функций принадлежности.
Для значений, соответствующих экстремальным значениям параметра, выбираются S- или Z-функции принадлежности.
Слайд 42
Алгоритмы нечеткого вывода
*
Среди других алгоритмов нечеткого вывода, пожалуй,
наиболее известными и популярными являются алгоритмы Мамдани (Mamdani) и
Сугэно (Sugeno).Алгоритм Мамдани. Отметим вначале, что используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:
П1: если x есть A1, тогда z есть B1,
П2: если x есть A2, тогда z есть B2,
. . . . . . . . . .
Пn: если x есть An, тогда z есть Bn,
где x - входная переменная (имя для известных значений данных), z - переменная вывода (имя для значения данных, которое будет вычислено); Аi и Вi - нечеткие множества.
Слайд 43
Алгоритм Сугэно
*
Исходный набор правил представляется в виде
Пi: если
x есть Ai, тогда z есть zi, i =
1,2,…,n,где zi = z(xi).
Приведем пример двух правил:
П1: если х есть А1 и y есть В1, то z1=a1x+b1y,
П2: если х есть А2 и y есть В2, то z2=a2x+b2y.
Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний. В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных.
Слайд 44
Алгоритм Сугэно
*
Алгоритм Сугэно (0-го порядка). Исходный набор правил
представляется в виде
Пi: если x есть Ai, тогда z
есть zi, i = 1,2,…,n, где zi = z(xi).
Алгоритм Сугэно с вычислительной точки зрения реализуется значительно проще, чем алгоритм Мамдани, а время счета для него меньше, чем для алгоритма Мамдани в 50-100 раз.
Общий вывод: если нет каких-либо особенных доводов в пользу алгоритма Мамдани, то лучше использовать не его, а алгоритм Сугэно.
Слайд 45
*
Метод выбора тестов при помощи алгоритма Сугено
mf1
= 25f+25d+50; mf2 = 22.5f+22.5d+45; mf3 = 20f+20d+40;
mf4 =
12.5f+12.5d+25; mf5 = 5f+5d+10; mf6 = 2.5f+2.5d+5; mf7 = 0;где f – вероятность проявления неисправности;
d – вероятность покрытия неисправности исследуемым тестом.
Слайд 46
*
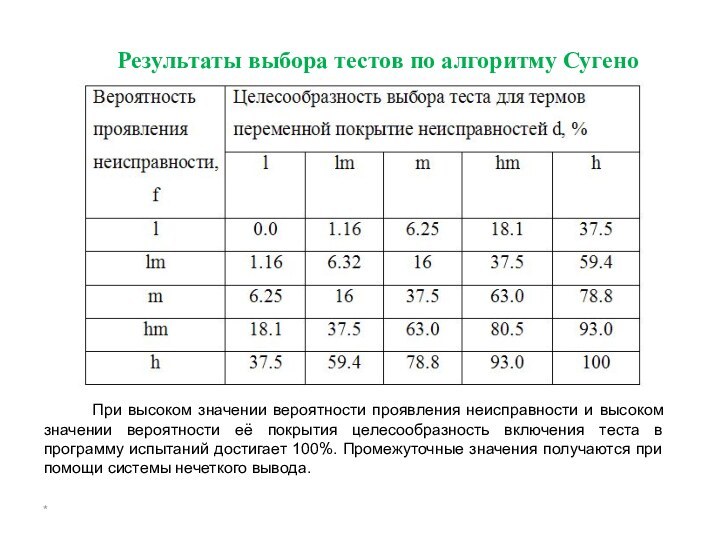
Результаты выбора тестов по алгоритму Сугено
При высоком значении вероятности проявления неисправности и
высоком значении вероятности её покрытия целесообразность включения теста в программу испытаний достигает 100%. Промежуточные значения получаются при помощи системы нечеткого вывода.
Слайд 47
Операции нечеткого вывода
*
Фаззификация (переход к нечеткости)
Точные значения входных
переменных преобразуются в значения лингвистических переменных посредством применения некоторых
положений теории нечетких множеств, а именно - при помощи определенных функций принадлежности.Дефаззификация (устранение нечеткости)
На этом этапе осуществляется переход от нечетких значений величин к определенным физическим параметрам, которые могут служить командами исполнительному устройству.
Слайд 49
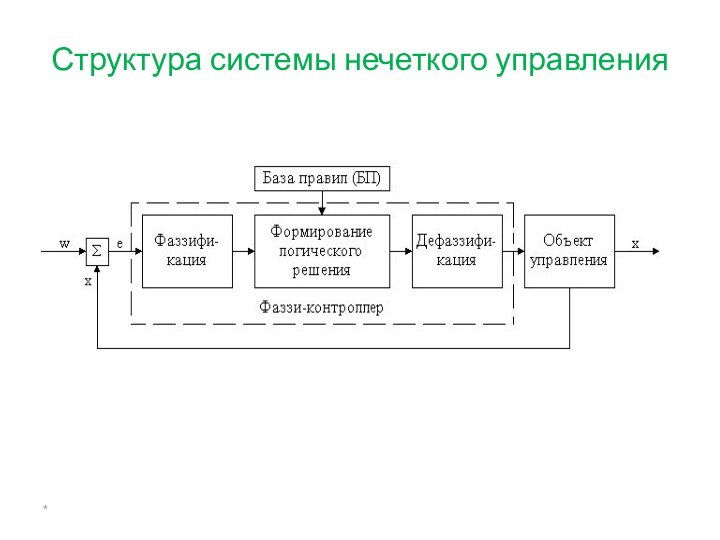
Моделирование работы светофора с нечеткой логикой
ПОСТАНОВКА:
В обычном светофоре время работы зеленого и красного света,
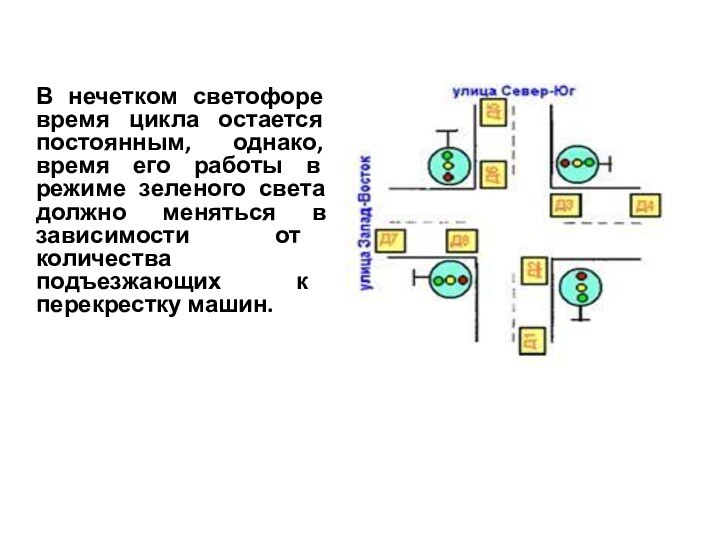
а также время цикла фиксированы. Это создает некоторые трудности в движении машин, особенно, при изменении их потоков в часы пик, что довольно часто приводит к появлению автомобильных пробок. Слайд 50 В нечетком светофоре время цикла остается постоянным, однако,
время его работы в режиме зеленого света должно меняться
в зависимости от количества подъезжающих к перекрестку машин.
Слайд 51
Светофор использует разности показаний четырех пар датчиков:
(Д1-Д2), (Д3-Д4), (Д5-Д6) и (Д7-Д8).
если
для улицы СЮ горит зеленый свет, машины проезжают перекресток и показания двух пар датчиков равны: Д1=Д2, Д5=Д6,
а, следовательно, их разность равна нулю.
В это же время на улице ЗВ перед светофором останавливаются машины, которые успели проехать только Д4 и Д7.
Суммарное количество автомобилей на этой улице :
(Д4-Д3)+(Д7-Д8)=(Д4-0)+(Д7-0)=Д4+Д7
Слайд 52 Показатель эффективности - число машин, не проехавших перекресток
за один цикл светофора.
Для каждой переменной надо задать лингвистические
термы, соответствующие некоторым диапазонам четких значений. Слайд 53 Для переменной время зеленого света предлагается три терма:
малое (10-25сек.);
среднее(20-40сек.);
большое(35-50сек.).
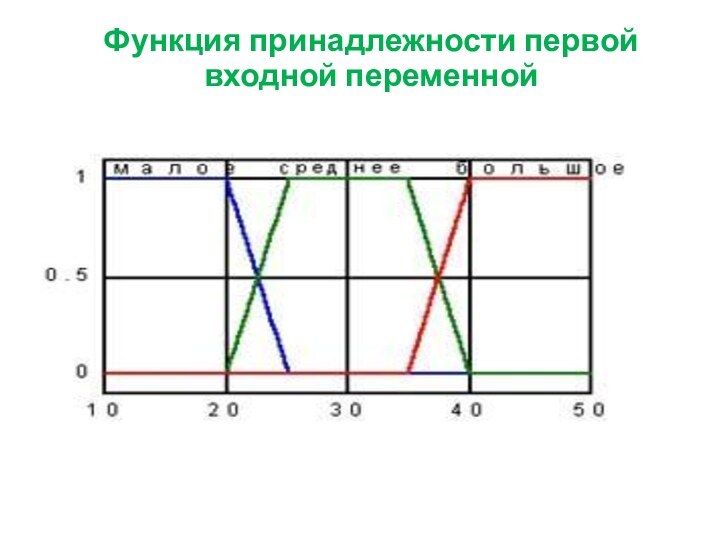
Слайд 55
Термы для двух оставшихся переменных :
очень малое (0-18);
малое (16-36);
среднее (34-56);
большое (54-76);
очень большое (72-90).
Слайд 56
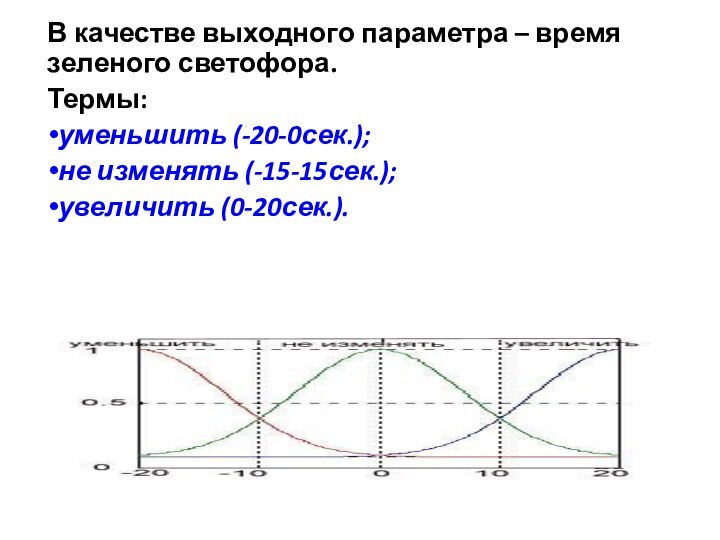
В качестве выходного параметра – время зеленого светофора.
Термы:
уменьшить (-20-0сек.);
не изменять (-15-15сек.);
увеличить (0-20сек.).
Слайд 57 Таблица правил на основе условных высказываний формирует выходное
значение:
Если (число машин на улице СЮ=малое)@(число машин на улице
ЗВ=большое)@ (время зеленого света на улице СЮ=большое), то (время зеленого света=уменьшить).
Слайд 58
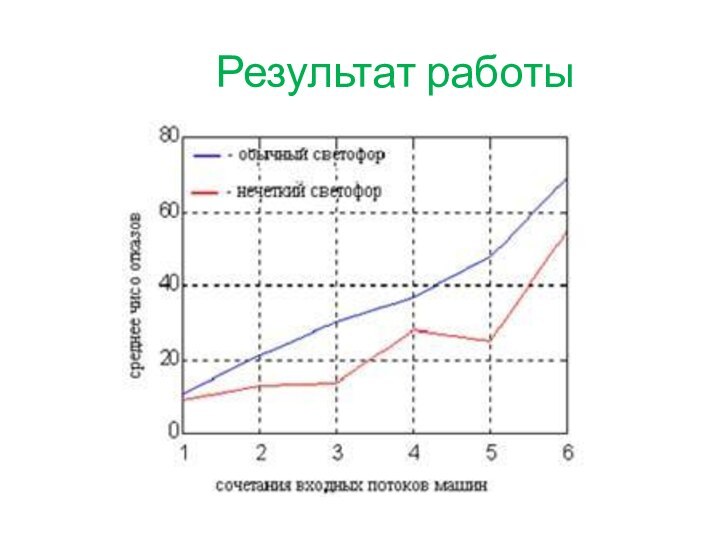
Результаты моделирования работы светофора с нечеткой логикой
На
светофор с датчиков поступает информация о количестве автомобилей на
двух улицах.Эти данные переводятся в нечеткий формат согласно заданным функциям принадлежности.
происходит их обработка, значение изменения времени зеленого света дефаззифицируется (т.е. переводится обратно в четкий формат) и поступает в виде управляющего сигнала на светофор.
В соответствии с этим сигналом время зеленого света светофора в следующем цикле будет другим.