Слайд 2
Определения
Для оценки сложности алгоритма используется O-символика.
На основе этой оценки можно привести следующую классификацию
алгоритмов, при размере входных данных, равном n:
постоянные – сложность не зависит от n: O(1);
линейные – сложность: O(n);
полиномиальные – сложность: O(nm), где m - константа;
экспоненциальные – сложность: O(tf(n)), где t – константа > 1, а f(n) – полиномиальная функция;
суперполиномиальные – сложность: O(сf(n)), где с – константа, а f(n) – функция, возрастающая быстрее постоянной, но медленнее линейной.
Слайд 3
Определения
Простые задачи (решаемые) – это задачи,
решаемые за полиномиальное время.
Труднорешаемые задачи –
это задачи, которые не решаются за полиномиальное время, либо алгоритм решения за полиномиальное время не найден.
Кроме того, как было доказано А. Тьюрингом, существуют принципиально неразрешимые задачи.
Сложность задач не определяется по сложности наилучшего алгоритма, её решающего. Для оценки сложности вводится классификация функций, вычисление которых возможно при задаваемых ограничениях на потребляемые ресурсы.
Слайд 4
Классификация задач
1. P-задачей (полиномиальной задачей) называется
задача, которую можно решить за полиномиальное (от длинны входа)
время.
2. NP-задачей (недетерминированно полиномиальной задачей) называется задача, которую можно решить только на недетерминированной машине Тьюринга, которая в отличие от обычной машины Тьюринга может делать предположения. Это задачи, у которых есть ответ, найти который трудно, но проверить можно за полиномиальное время.
Слайд 5
Классификация задач
3. NP-полной называется задача из
класса NP, к которой можно свести любую другую задачу
из класса NP за полиномиальное время. Таким образом, NP-полные задачи образуют в некотором смысле подмножество «самых сложных» задач в классе NP.
И если для какой-то из них будет найден «быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
Нахождение алгоритма, решающего какую-либо NP-полную задачу за полиномиальное время позволит находить решения NP-задач за полиномиальное время, то есть позволит считать их P-задачами.
Слайд 6
Классификация задач
4. Класс EXPTIME – класс
задач, решаемых за экспоненциальное время.
5. Класс
EXPTIME-полных задач – класс задач, которые не решаются за детерминированное полиномиальное время. Известно, что P <> EXPTIME.
Класс P входит в NP, но проверить, что
P ≠ NP или P = NP до сих пор не удалось. Примеры NP-полных задач
Задача коммивояжёра
Кратчайшее решение “пятнашек” размера nxn
Проблема раскраски графа
и др.
Слайд 7
Задача коммивояжера
Имеется n пунктов, расстояния между
которыми известны. Требуется объехать все пункты, посетив каждый по
одному разу и возвратиться в исходный пункт, при этом длина маршрута была бы наименьшей.
Общее число обходов n пунктов = (n-1)!/2. Решая эту задачу методом перебора всех возможных кольцевых маршрутов и выбора из них самого короткого, нужно выполнить столько же итераций. Данный метод решения делает задачу коммивояжера NP-полной задачей.
Примем n=100. Для решения задачи потребуется выполнить не менее 1021 операций. Учитывая скорость современных компьютеров, на это потребуется около 30 лет.
В настоящее время полиномиальное решение задачи коммивояжера неизвестно.
Слайд 8
Методы разработки алгоритмов
Рассмотрим несколько методов:
Метод декомпозиции (пример: игра
“Ханойская башня”).
Динамическое программирование.
Поиск с возвратом (пример: расстановка ферзей на
шахматной доске, обход конём шахматной доски).
Метод ветвей и границ.
Метод альфа-бета отсечения.
и др.
Слайд 9
Метод декомпозиции
Этот метод имеет также название
«разделяй и властвуй» или метод разбиения. Этот метод наиболее
применим для проектирования эффективных алгоритмов.
Он предлагает такую декомпозицию (разбиение) задач размера n на более мелкие задачи, что на основе решения этих более мелких задач можно получить решение исходной задачи.
Примеры: сортировка слиянием или применение деревьев двоичного поиска.
Рассмотрим игру «Ханойская башня».
А
В
С
Слайд 10
Ханойская башня
Даны три стержня, на один
из которых нанизаны n колец, причем кольца отличаются размером
и лежат меньшее на большем. Задача состоит в том, чтобы перенести пирамиду из n колец за наименьшее число ходов со стержня А на В. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее. Стержень С можно использовать для временного хранения дисков. Эту известную игру придумал французский математик Эдуард Люка, в 1883 году.
Количество перекладываний в зависимости от количества колец (n) вычисляется по формуле
Задачу перемещения n дисков со стержня А на стержень В можно разбить на две подзадачи размера n-1. Сначала нужно переместить n-1 наименьших дисков со стержня А на стержень С, оставив на стержне А n-й наибольший диск. Затем этот диск перекладываем с А на В. Потом перемещаем n-1 диск с С на В и т.д.
Слайд 11
Динамическое программирование
Идея: чтобы решить поставленную задачу,
требуется решить отдельные части задачи (подзадачи), после чего объединить
решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
Рассмотрим пример чисел Фибоначчи: 1,1,2,3,5,8,11… При вычислении 6-7 десятка чисел современным вычислительным машинам не хватает временных ресурсов.
Формулы вычисления: и т.д.
содержат вычисления одних и тех же значений многократно, т.е. решаются подзадачи, которые уже были решены.
Слайд 12
Динамическое программирование
Формулы вычисления:
и т.д.
содержат вычисления одних и тех же значений многократно, т.е. решаются подзадачи, которые уже были решены.
Чтобы исключить повторный счёт, будем сохранять решения подзадач, которые уже решали, и когда они снова потребуется - просто достанем их из памяти. Для дальнейшей оптимизации, подзадачи, которые понадобятся в дальнейшем, можно решить заранее.
Динамическое программирование пользуется следующими свойствами задачи:
перекрывающиеся подзадачи;
оптимальная подструктура;
возможность запоминания решения часто встречающихся подзадач.
Слайд 13
Динамическое программирование
Динамическое программирование обычно придерживается двух
подходов:
нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера,
они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.
восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи, решаются заранее и затем используются для построения решения исходной задачи. Исходная задача представляется в виде рекурсивной последовательности более простых подзадач.
Слайд 14
Поиск с возвратом
Это метод нахождения решения
задачи, в которой требуется полный перебор всех возможных вариантов в
некотором множестве.
Решение задачи методом поиска с возвратом сводится к последовательному расширению частичного решения. Если на очередном шаге такое расширение провести не удается, то возвращаются к более короткому частичному решению и продолжают поиск дальше. Для ускорения метода стараются вычисления организовать таким образом, чтобы как можно раньше выявлять заведомо неподходящие варианты. Часто это позволяет значительно уменьшить время нахождения решения.
Слайд 15
Поиск с возвратом
Незначительные модификации метода
поиска с возвратом, связанные с представлением данных или особенностями
реализации, имеют и иные названия: метод ветвей и границ, поиск в глубину, метод проб и ошибок и т. д.
Метод поиска с возвратом применяется при решении задач «искусственного интеллекта». Решение в этих задачах осуществляется не по заданным правилам вычислений, а методом проб и ошибок. Часто применяется метод рекурсии, который требует исследования конечного числа подзадач.
В результате процесса поиска строится (и обрезается) дерево подзадач, рост этого дерева часто бывает экспоненциальным. Иногда используют некоторые эвристики (алгоритм, не имеющий строгого обоснования, но, тем не менее, дающий приемлемое решение задачи).
Слайд 16
Обход конём шахматной доски
Задача. На
шахматной доске размера nxn в позиции (x0, y0) находится
конь. Составить рекурсивную программу, находящую методом перебора с возвратом обход конём доски с конкретного поля, т.е. получить такую последовательность ходов, при которой конь точно один раз побывает на всех полях доски, т.е. нужно вычислить n² - 1 ходов.
Для доски 8x8 эта задача впервые была поставлена Л.Эйлером.
Все шаги фиксируются таким образом, что позже можно вернуться «вспять», отбрасывая тем самым шаги, которые ведут в тупик. Такой процесс называется возвратом или откатом.
Слайд 17
Обход конём шахматной доски
Создадим
массивы a[1..8], B[1..8] и занесём в них возможные ходы коня:
a: 2, 1, -1, -2, -2, -1, 1, 2
b: 1, 2, 2, 1, -1, -2, -2, -1
Возможные решения (при n=5):
10 15 4 25 23 4 9 14 25
5 24 9 14 10 15 24 1 8
22 1 18 3 5 22 3 18 13
6 17 20 13 8 16 11 20 7 2
21 12 7 2 19 21 6 17 12 19
Слайд 18
Метод ветвей и границ
Впервые метод ветвей
и границ был предложен Лендом и Дойгом в 1960
для решения общей задачи целочисленного линейного программирования.
В основе метода лежит идея последовательного разбиения множества допустимых решений на подмножества (стратегия “разделяй и властвуй”). На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет.
Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено.
Слайд 19
Метод ветвей и границ
Если значение
целевой функции на найденном решении меньше рекорда, то происходит
смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы.
Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.
Метод используется для решения некоторых
NP-полных задач, таких как:
задача коммивояжёра,
задача о ранце.
Слайд 20
Метод альфа-бета отсечения
Метод «ветвей и границ»
можно ещё улучшить, если ввести не одну оценку, а
две, т.е. верхнюю и нижнюю границы. Это так называемая минимаксная альфа-бета процедура или просто альфа-бета отсечение. Этот метод является значительным продвижением по сравнению с односторонним методом «ветвей и границ».
В основе алгоритма лежит идея, что оценивание ветви дерева поиска может быть досрочно прекращено (без вычисления всех значений оценивающей функции), если было найдено, что для этой ветви значение оценивающей функции в любом случае хуже, чем вычисленное для предыдущей ветви.
Так как отсечения происходят на каждом уровне вложенности (кроме последнего), эффект может быть весьма значительным.
Слайд 21
Повторение:
- Алгоритмы работы с графами
- Поиск в тексте
-
Кодирование и сжатие данных
Слайд 22
Поиск в глубину (порядок обхода)
Поиск в глубину для
полного обхода графа с n вершинами и m дугами
требует общего времени порядка O(max(n, m)). Поскольку обычно m≥n, то получается O(m). Используется стек.
Слайд 23
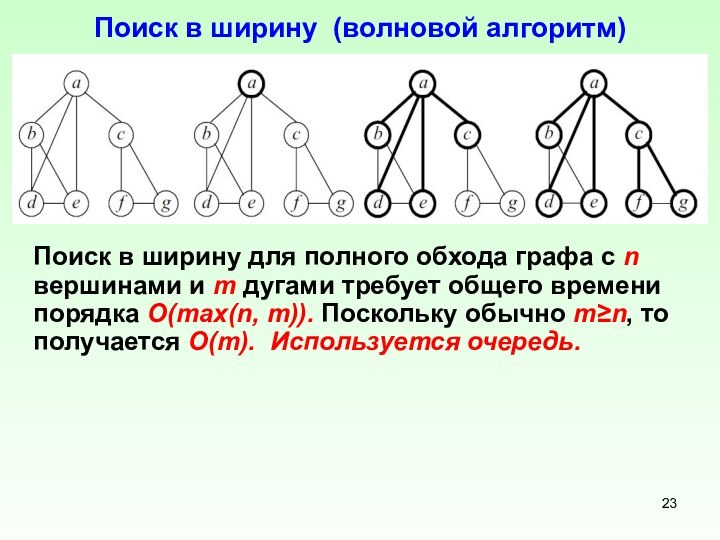
Поиск в ширину (волновой алгоритм)
Поиск в ширину для
полного обхода графа с n вершинами и m дугами
требует общего времени порядка O(max(n, m)). Поскольку обычно m≥n, то получается O(m). Используется очередь.
Слайд 24
Топологическая сортировка (ТС)
Это сортировка элементов,
для которых определено отношение частичного порядка, т.е. порядок задан
не для всех, а только лишь для некоторых пар.
Все стрелки смотрят направо, следовательно нужный порядок найден. В данной задаче отсутствуют циклы.
Слайд 25
Кратчайшие пути в графе
Задача 1:
Поиск
кратчайшего расстояния от одной из вершин графа до всех
остальных.
Рассмотрим взвешенный граф ОГ G=(V,E) с весовой функцией, которая сопоставляет каждому ребру графа некоторый вес – действительное число. Вес пути = сумме весов входящих в этот путь рёбер.
Вес кратчайшего пути из одной вершины в другую определяется как min значение веса пути среди всех возможных путей, соединяющих эти две вершины; если такого пути нет, считается, что вес кратчайшего пути =
Алгоритм Дейкстры – это алгоритм нахождения кратчайшего пути от одной из вершин графа до всех остальных (работает только для графов без ребер отрицательного веса).
Слайд 27
Кратчайшие пути в графе
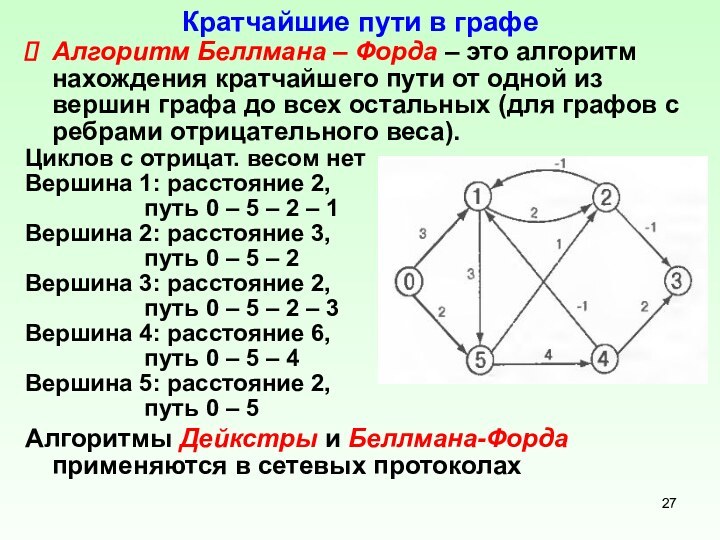
Алгоритм Беллмана – Форда –
это алгоритм нахождения кратчайшего пути от одной из вершин
графа до всех остальных (для графов с ребрами отрицательного веса).
Циклов с отрицат. весом нет
Вершина 1: расстояние 2,
путь 0 – 5 – 2 – 1
Вершина 2: расстояние 3,
путь 0 – 5 – 2
Вершина 3: расстояние 2,
путь 0 – 5 – 2 – 3
Вершина 4: расстояние 6,
путь 0 – 5 – 4
Вершина 5: расстояние 2,
путь 0 – 5
Алгоритмы Дейкстры и Беллмана-Форда применяются в сетевых протоколах
Слайд 28
Кратчайшие пути в графе
Задача 2:
Поиск
кратчайших путей между всеми парами вершин графа (без циклов
с отрицательными весами).
Если граф не содержит рёбер с отрицательным весом, то можно использовать алгоритм Дейкстры для нахождения кратчайшего пути от одной вершины до всех остальных, запустив его на каждой вершине.
Если же есть рёбра с отрицательным весом, можно использовать алгоритм Беллмана-Форда. Но этот алгоритм, запущенный на всех вершинах графа, работает медленнее.
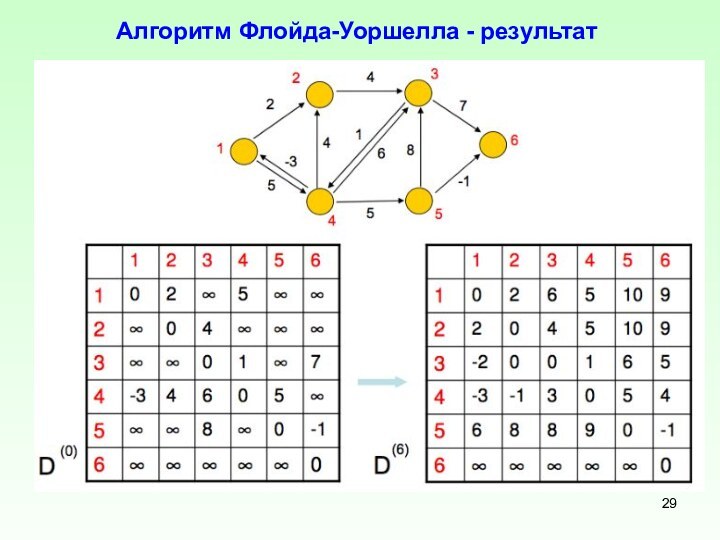
Алгоритм Флойда-Уоршелла – это алгоритм поиска кратчайшего пути между любыми двумя вершинами графа.
Использование – транспортные сети, генетика …
Слайд 29
Алгоритм Флойда-Уоршелла - результат
Слайд 30
Переборные алгоритмы
Задача 3:
Переборные алгоритмы основаны
на методах обхода графа. Поскольку существует два метода обхода
графа, то и переборных алгоритмов существует два (на примере задачи нахождения кратчайшего пути в лабиринте).
Лабиринт, состоящий из проходимых и непроходимых клеток, задан матрицей A размером mxn. Элемент матрицы A[i,j]=0, если клетка (i,j) проходима. В противном случае A[i,j]= .
Требуется найти длину кратчайшего пути из клетки (1, 1) в клетку (m, n).
Лабиринт представляет собой граф. Задачу будем решать методом перебора с возвратом (поиск в глубину).
Слайд 31
Переборный алгоритм (поиска в глубину)
Слайд 32
Поиск в тексте
Пусть задан массив
Txt из n элементов, называемый текстом и массив Wrd
из m элементов, называемый словом, причём 0 < m ≤ n. Описать их можно как строки.
Поиск слова обнаруживает первое вхождение Wrd в Txt. Этот поиск присутствует в любых системах обработки текстов, поэтому необходимо искать эффективный алгоритм для решения этой задачи.
Изученные алгоритмы:
прямого поиска, сложность - O((n-m+1)xm);
Кнута, Морриса и Пратта, сложность - O(m+n);
Боуера, Мура, Хорспула, сложность в наихудшем случае – O(m*n), но для случайных текстов – O(n),
где n и m – длины строки и подстроки.
Слайд 33
Алгоритм Кнута, Морриса и Пратта
Алгоритм
основывается на том факте, что после частичного совпадения начальной
части подстроки с соответствующими символами строки фактически известна пройденная часть строки и можно вычислить некоторые сведения, с помощью которых затем быстро продвинуться по строке.
Сдвиг подстроки выполняется не на один символ на каждом шаге алгоритма, а на некоторое переменное количество символов.
Так как величины сдвига зависят только от слова, то перед началом фактического поиска можно вычислить вспомогательную таблицу.
Слайд 34
Алгоритм Боуера, Мура, Хорспула
Алгоритм БМХ
считается наиболее быстрым среди алгоритмов, предназначенных для поиска подстроки
в строке. Он был разработан в 1977 году. Преимущество этого алгоритма в том, что необходимо сделать некоторые предварительные вычисления над подстрокой, чтобы сравнение подстроки с исходной строкой осуществлять не во всех позициях – часть проверок пропускаются как заведомо не дающих результата.
Сравнение символов начинается с конца слова. Перед фактическим поиском на основе слова формируется некоторая таблица.
Слайд 35
Сжатие данных
Степень избыточности данных зависит
от типа данных. Другим фактором, влияющим на степень избыточности
является принятая система кодирования. Примером систем кодирования могут быть обычные языки общения.
При хранении и передаче информации средствами компьютерной техники, избыточность играет отрицательную роль, поскольку она приводит к возрастанию стоимости хранения и передачи информации. Постоянно возникает проблема уменьшения избыточности или сжатия данных. Если методы сжатия данных применяются к готовым файлам, то часто вместо термина "сжатие данных" употребляют термин "архивация данных".
Слайд 36
Способы уменьшения избыточности данных:
Изменение содержимого данных.
Изменение структуры данных.
Одновременное
изменение как структуры, так и содержимого данных.
Если при сжатии данных происходит изменение их содержимого, то метод сжатия называется необратимым, то есть при восстановлении (разархивировании) данных из архива не происходит полного восстановления информации. Такие методы часто называются методами сжатия с регулированными потерями информации.
Такие методы применяются к следующим типам данных видео- (MPG) и аудио- (MP3), а также графическим данным (JPEG), но их нельзя применять к текстовым данным.
Слайд 37
Обратимые методы
Если при сжатии данных
происходит только изменение структуры данных, то метод сжатия называется
обратимым. В этом случае, из архива можно восстановить информацию полностью. Обратимые методы сжатия можно применять к любым типам данных, но они дают меньшую степень сжатия по сравнению с необратимыми методами сжатия. Форматы сжатия без потерь:
GIF, TIFF - для графических данных;
AVI - для видеоданных;
ZIP, ARJ, RAR, CAB, LH - для произвольных типов данных.
Методы сжатия без потери информации:
метод Хаффмана;
арифметическое сжатие;
PPM (метод контексного моделирования);
BWT (MTF) – сжатие с использованием преобразования Барроуза-Уилера.
Слайд 38
Методы сжатия без потери информации
Методы сжатия
без потерь делятся на две категории:
1. Статистические методы –
методы сжатия, присваивающие коды переменной длины символам входного потока, причем более короткие коды присваиваются символам или группам символам, имеющим большую вероятность появления во входном потоке:
сжатие по Хаффману,- самый известный и распространённый метод,
арифметическое сжатие,- наилучший на сегодняшний день метод по степени сжатия,
сжатие с кодами Райса-Голомба,- компромисс между методом Хаффмана и Арифметическим методом,
и др.