- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основные понятия теории графов
Содержание
- 2. 1. Базовое определение графа и его составляющих2.Пути, маршруты, цепи и циклы3.Подграфы4.Список литературыОглавление
- 3. Граф - это множество точек или вершин и
- 4. Графы обычно изображаются в виде геометрических фигур,
- 5. Путь — это последовательность дуг, в которой конечная
- 6. Построим граф, изображающий отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}.
- 7. Подграф графа - это граф, являющийся подмоделью исходного графа, т.е.
- 8. Дерево — это связный граф без циклов. Деревья
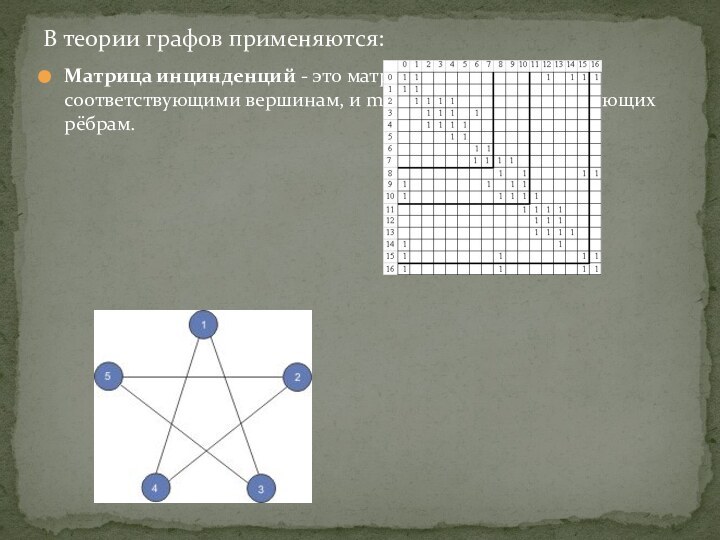
- 9. Матрица инцинденций - это матрица А с n строками, соответствующими вершинам,
- 10. http://matmetod-popova.narod.ru/theme213.htmhttp://www.algolib.narod.ru/Graph/Base.htmlhttp://lib.vvsu.ru/books/Bakalavr01/page0221.asphttp://dmtsoft.ru/bn/391/as/oneaticleshablon/Список использованной литературы:
- 11. Скачать презентацию
- 12. Похожие презентации
1. Базовое определение графа и его составляющих2.Пути, маршруты, цепи и циклы3.Подграфы4.Список литературыОглавление


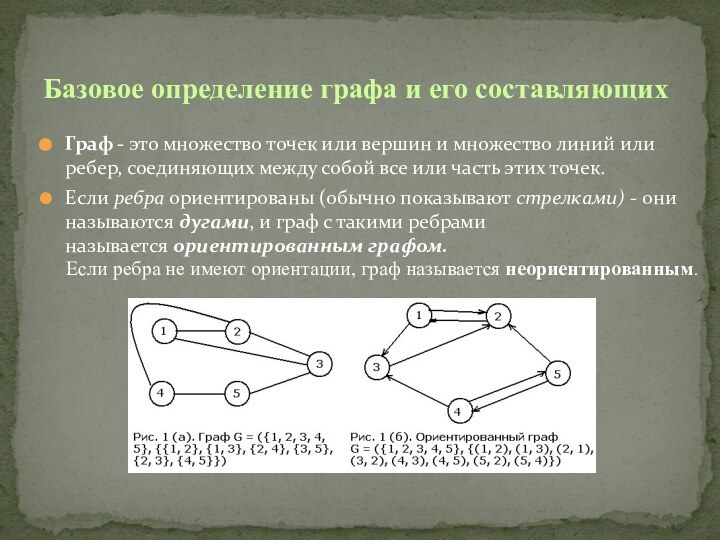



Слайд 3 Граф - это множество точек или вершин и множество
линий или ребер, соединяющих между собой все или часть
этих точек.Если ребра ориентированы (обычно показывают стрелками) - они называются дугами, и граф с такими ребрами называется ориентированным графом.
Базовое определение графа и его составляющих
Если ребра не имеют ориентации, граф называется неориентированным.
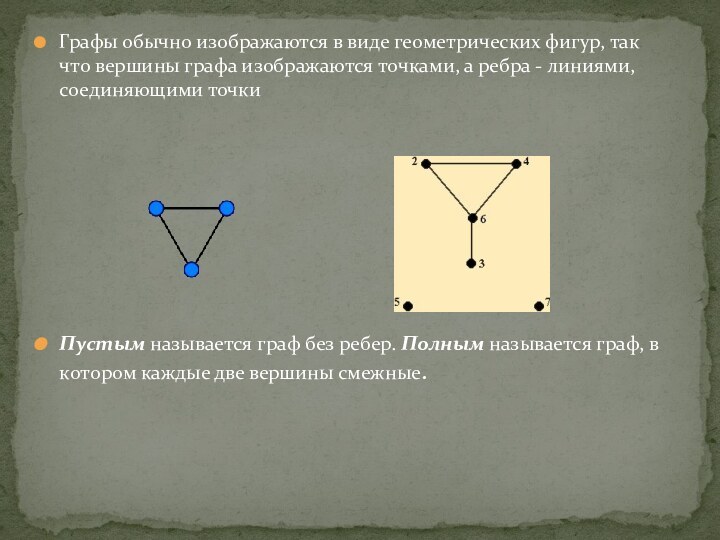
Слайд 4 Графы обычно изображаются в виде геометрических фигур, так
что вершины графа изображаются точками, а ребра - линиями,
соединяющими точкиПустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.
Слайд 5 Путь — это последовательность дуг, в которой конечная вершина
всякой дуги, отличной от последней, является начальной вершиной следующей.
Маршрут –
это путь, ориентацией дуг которого можно пренебречь.
Цепь – это маршрут, в котором все ребра попарно различны.
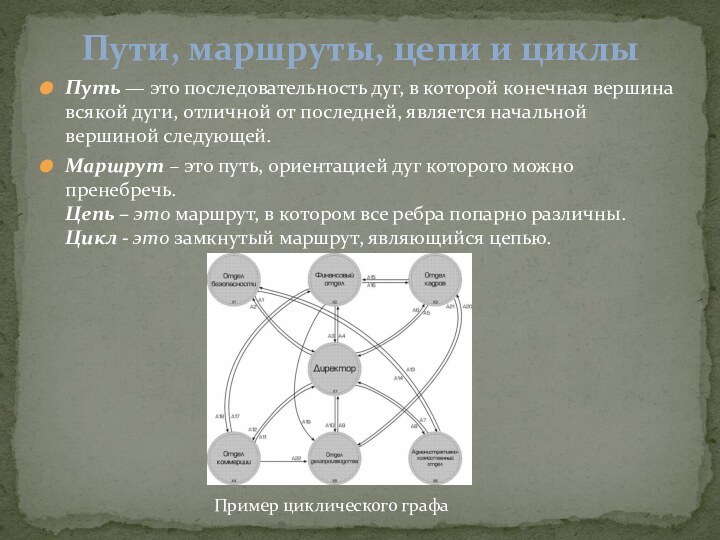
Цикл - это замкнутый маршрут, являющийся цепью.Пути, маршруты, цепи и циклы
Пример циклического графа
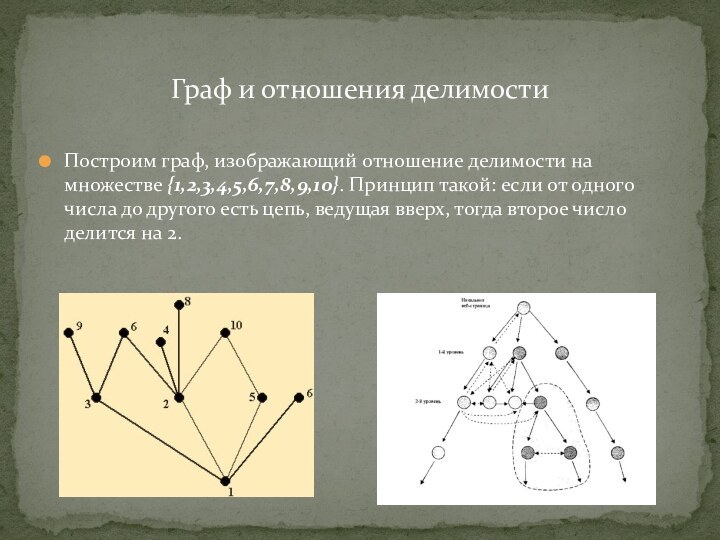
Слайд 6 Построим граф, изображающий отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}. Принцип
такой: если от одного числа до другого есть цепь,
ведущая вверх, тогда второе число делится на 2.Граф и отношения делимости
Слайд 7 Подграф графа - это граф, являющийся подмоделью исходного графа, т.е. подграф
содержит некоторые вершины исходного графа и некоторые ребра.
Подграф, порожденный
множеством вершин U – это подграф, множество вершин которого - U содержащий те и только те ребра, оба конца которых входят в U.Граф называется связным, если любая пара его вершин связана. Связными компонентами графа называются подграфы данного графа, вершины которых связаны.
Подграфы
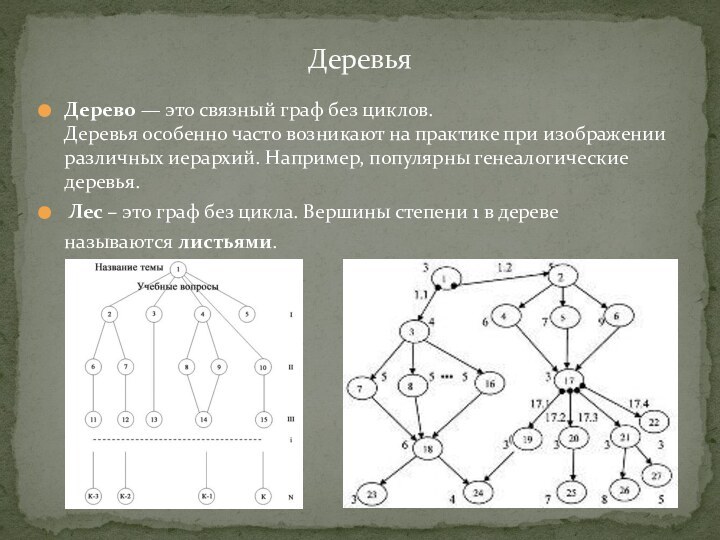
Слайд 8 Дерево — это связный граф без циклов. Деревья особенно часто
возникают на практике при изображении различных иерархий. Например, популярны
генеалогические деревья.Лес – это граф без цикла. Вершины степени 1 в дереве называются листьями.
Деревья
Слайд 9 Матрица инцинденций - это матрица А с n строками, соответствующими вершинам, и m столбцами,
соответствующих рёбрам.
Матрица смежности - это матрица n×n где n - число вершин,
где bij = 1, если существует ребро, идещее из вершины х в вершину у и bij = 0 в противном случае.В теории графов применяются: